点云深度学习——pyqt调用配准网络DCP模型
点云深度学习——pyqt调用配准网络DCP模型
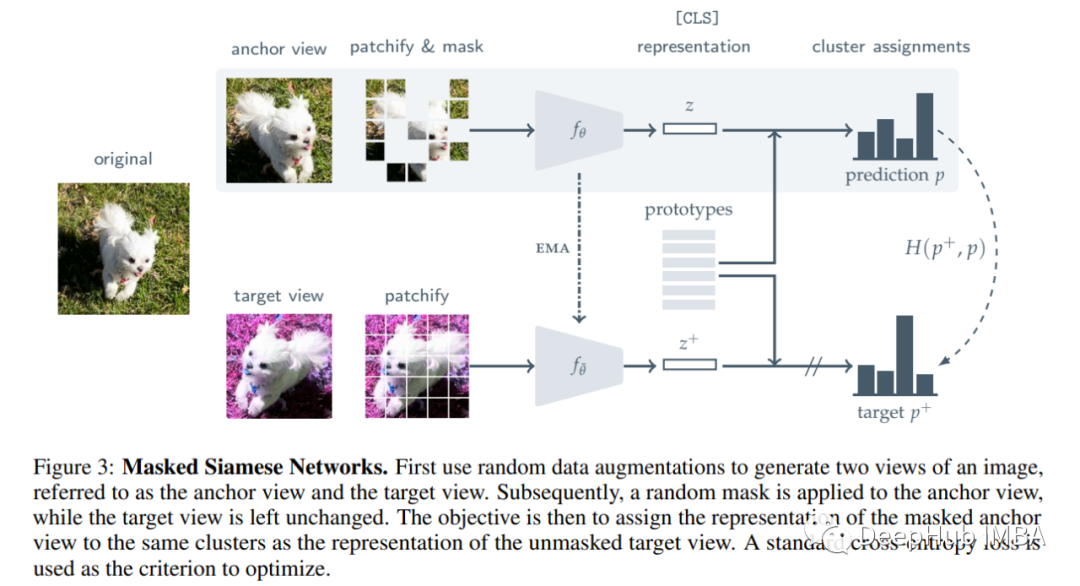
论文推荐:使用带掩码的孪生网络进行自监督学习
本篇文章将介绍Masked Siamese Networks (MSN),这是另一种用于学习图像表示的自监督学习框架。MSN 在 ImageNet-1K 上的线性评估方面优于 MAE 和其他模型
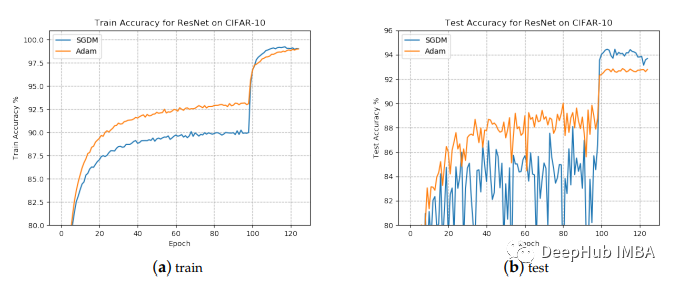
为什么Adam 不是默认的优化算法?
本文这并不是否定自适应梯度方法在神经网络框架中的学习参数的贡献。而是希望能够在使用Adam的同时实验SGD和其他非自适应梯度方法
卷积神经网络CNN实现mnist手写数字识别
卷积神经网络CNN实现mnist手写数字识别
【深度学习】基于卷积神经网络(tensorflow)的人脸识别项目(四)
实现一个基于界面化的一个人脸识别。本篇主要是实现第四步。最后一篇咯 1. 首先需要收集数据,我的想法是通过OpenCV调用摄像头进行收集人脸照片。 2. 然后进行预处理,主要是对对数据集分类,训练集、验证集、测试集。选取合适的参数,例如损失函数。图像灰度化、归一化等等操作。 3. 开始训练模型,提前
RepVGG :让卷积再次伟大
一个经典的卷积神经网络(ConvNet),VGG [31],在图像识别方面取得了巨大的成功,其简单的架构由一堆 conv、ReLU 和 pooling 组成。随着 Inception [33, 34, 32, 19]、ResNet [12] 和 DenseNet [17],许多研究兴趣转移到精心设计

使用Pytorch手写ViT — VisionTransformer
本篇文章使用 Pytorch 中实现 Vision Transformer,通过我们自己的手动实现可以更好的理解ViT的架构
【深度学习实践(八)】生成对抗网络(GAN)之手写数字生成
【深度学习实践(八)】生成对抗网络(GAN)之手写数字生成
刘二大人 PyTorch深度学习实践 笔记 P7 处理多维特征的输入
刘二大人 PyTorch深度学习实践 笔记 P7 处理多维特征的输入
【深度学习】5-从计算图直观认识“激活函数不以零为中心导致收敛变慢”
关于激活函数以零为中心问题的较直观解释,并于参数值全相同的问题做了对比。
数学建模(三):预测
数学建模(三):预测
【深度学习】SVM与百度飞桨
SVM和KNN都是对分类数据点进行距离的计算,距离计算公式(二范数)是np.sqare (np.pow ( (x1-x2),2)),即根号下两点差的平方。SVM要比KNN分类效果一般要好,并且速度要快。
基于YOLOV7的openpose人体姿态检测识别,FPS可以达到“较高”的效果
前不久yolov7(原yolov4团队)在yolov6(美团)开源不到两周的时间也更新了,如下图所示,yolov7效果比前面的版本确实牛逼,在精度相同的情况下,速度上面提升了一大截,但是这是在比较好的设备上面;YOLOv7 的发展方向与当前主流的实时目标检测器不同,研究团队希望它能够同时支持移动 G
【深度学习】基于卷积神经网络(tensorflow)的人脸识别项目(二)
实现一个基于界面化的一个人脸识别。本篇主要是实现第二步。 1. 首先需要收集数据,我的想法是通过OpenCV调用摄像头进行收集人脸照片。 2. 然后进行预处理,主要是对对数据集分类,训练集、验证集、测试集。选取合适的参数,例如损失函数。图像灰度化、归一化等等操作。 3. 开始训练模型,提前创建好标签
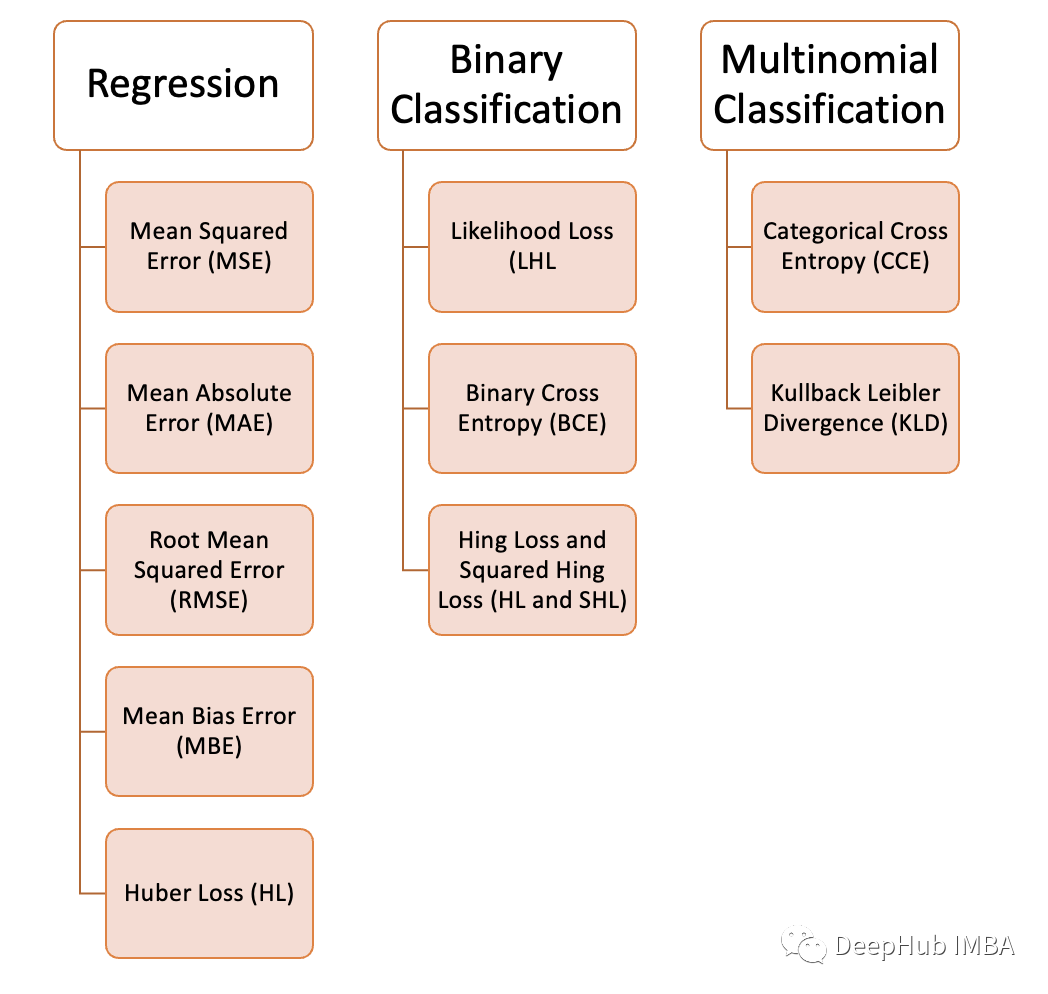
10个常用的损失函数解释以及Python代码实现
理解机器学习中的损失函数
【深度学习】4-梯度确认时遇bug:写了个糟糕的softmax函数
记录一个softmax函数没写好,未考虑批量处理情况导致的问题。
【深度学习前沿应用】文本分类Fine-Tunning
【自然语言处理(NLP)】基于GRU实现情感分类,基于百度飞桨开发,参考于《机器学习实践》所作。
数学建模(二):优化
数学建模(二):优化
有效涨点!用于低分辨率图像和小物体的新 CNN 模块SPD-Conv
卷积神经网络(CNN)在图像分类、目标检测等计算机视觉任务中取得了巨大的成功。然而,在图像分辨率较低或对象较小的更困难的任务中,它们的性能会迅速下降。这源于现有CNN体系结构中一个有缺陷但却很常见的设计,即使用和/或池化层,这导致了细粒度信息的丢失和较低效率的特征表示的学习。为此,我们提出了一种新的
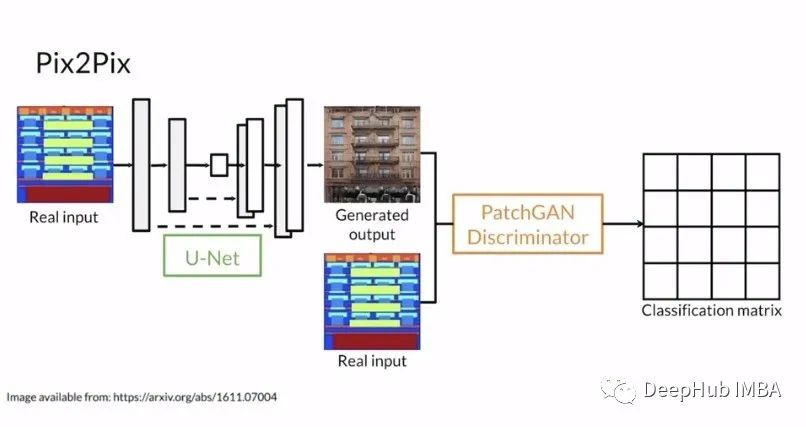
使用PyTorch和Keras实现 pix2pix GAN
对比两个框架实现同一个模型到底有什么区别?