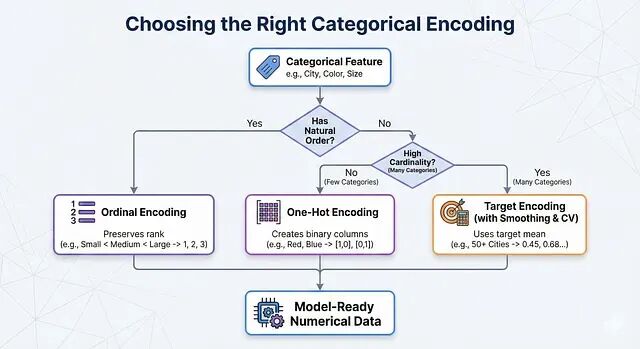
机器学习特征工程:分类变量的数值化处理方法
实际操作中可以这样判断:特征有天然顺序就用 Ordinal Encoding;没有顺序、类别数量也不多就用 One-Hot Encoding;类别太多就上 Target Encoding,记得配合 Smoothing 和交叉验证。
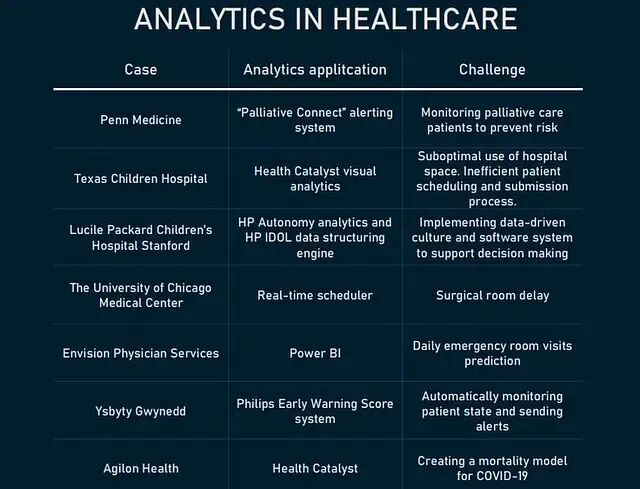
分类数据 EDA 实战:如何发现隐藏的层次结构
这篇文章讲的是如何在 EDA 阶段把这些隐藏结构找出来,用实际的步骤、真实的案例,外加可以直接复用的 Python 代码。
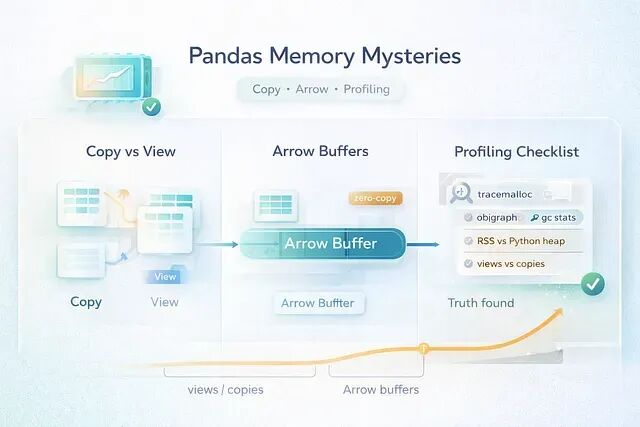
pandas 3.0 内存调试指南:学会区分真假内存泄漏
在pandas 3.0 之后这类情况更多了,因为Copy-on-Write 改变了数据共享的方式,Arrow 支持的 dtype 让内存行为变得更难预测。
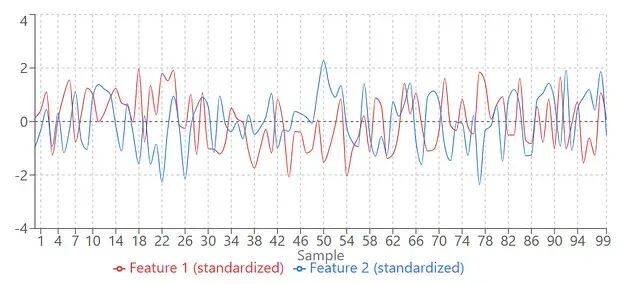
为什么标准化要用均值0和方差1?
为什么标准化要把均值设为0、方差设为1?
使用 tsfresh 和 AutoML 进行时间序列特征工程
本文将介绍多步时间序列预测的构建方式、auto-sklearn 如何扩展用于时间序列、tsfresh 的工作原理和使用方法

机器学习时间特征处理:循环编码(Cyclical Encoding)与其在预测模型中的应用
使用正弦和余弦进行循环编码,是一种优雅且低成本的修正手段。它保留了数据的邻近性,消除了人工伪影,能让模型学得更快、更准。
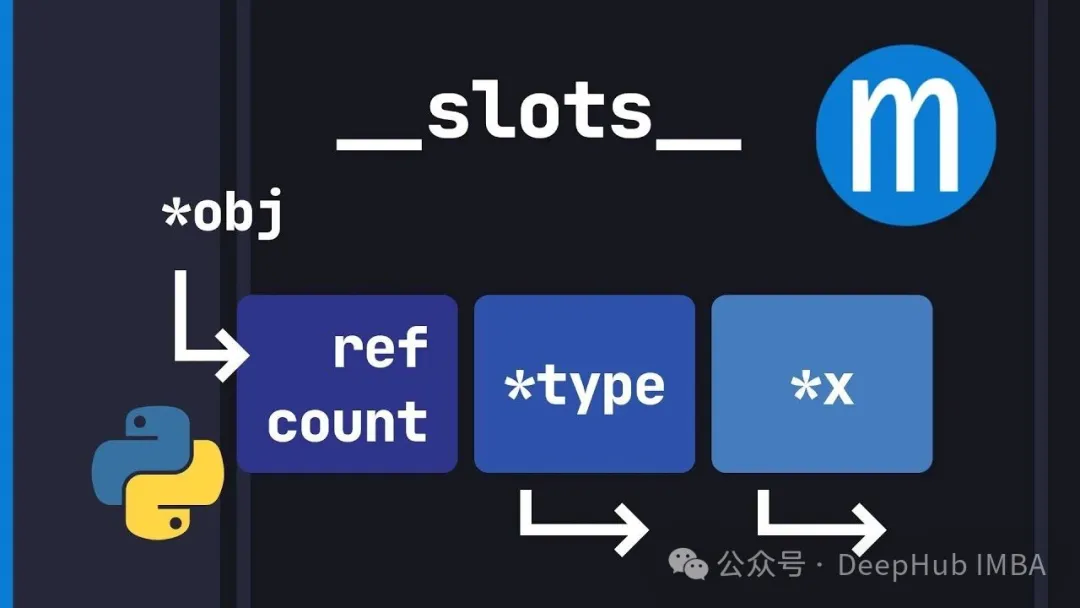
别再浪费内存了:Python __slots__ 机制深入解析
`__slots__` 就是让你用灵活性换内存效率和更快的属性访问。对于高性能场景来说这是个必须掌握的优化手段。

Scikit-Learn 1.8引入 Array API,支持 PyTorch 与 CuPy 张量的原生 GPU 加速
Scikit-Learn 1.8.0 更新引入了实验性的 Array API 支持。这意味着 CuPy 数组或 PyTorch 张量现在可以直接在 Scikit-Learn 的部分组件中直接使用了

PyCausalSim:基于模拟的因果发现的Python框架
今天介绍一下 **PyCausalSim**,这是一个利用模拟方法来挖掘和验证数据中因果关系的 Python 框架。
别只会One-Hot了!20种分类编码技巧让你的特征工程更专业
编码方法其实非常多。目标编码、CatBoost编码、James-Stein编码这些高级技术,用对了能给模型带来质的飞跃,尤其面对高基数特征的时候。

从 Pandas 转向 Polars:新手常见的10 个问题与优化建议
Polars 速度快、语法现代、表达力强,但很多人刚上手就把它当 Pandas 用,结果性能优势全都浪费了。
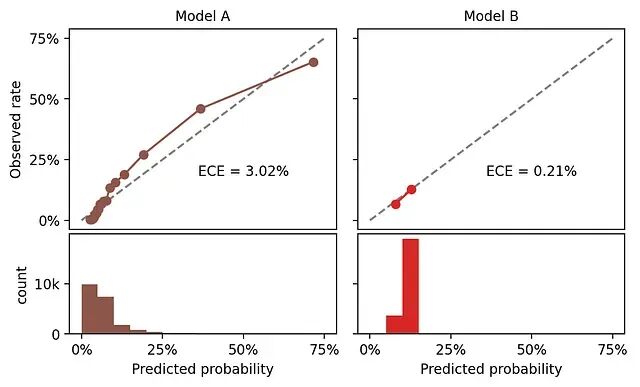
分类模型校准:ROC-AUC不够?用ECE/pMAD评估概率质量
这里校准的定义是:如果模型给一批样本都预测了25%的正例概率,那这批样本中实际的正例比例应该接近25%。这就是校准。

Pandas GroupBy 的 10 个实用技巧
本文将介绍10个实际工作中比较有用的技巧,文章的代码都是可以直接拿来用。

Python 3.14 实用技巧:10个让代码更清晰的小改进
Python 3.14 引入的改进大多数都很细微,但这些小变化会让代码写起来更流畅,运行也更稳定。本文整理了 10 个实用的特性改进,每个都配了代码示例。
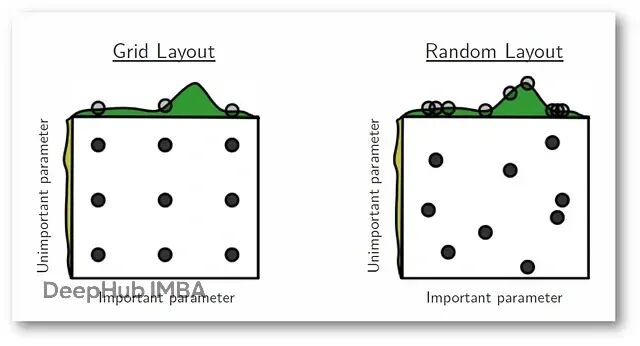
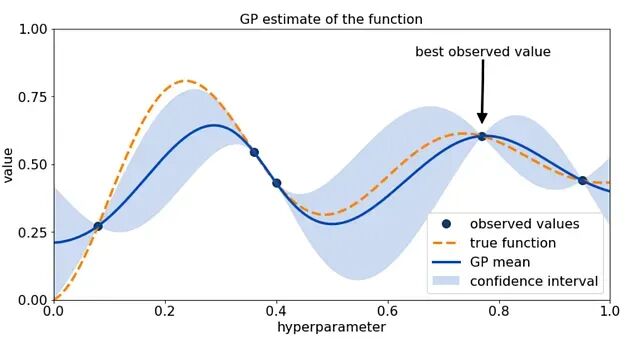
超参数调优:Grid Search 和 Random Search 的实战对比
这篇文章会把Grid Search和Random Search这两种最常用的超参数优化方法进行详细的解释。从理论到数学推导,从优缺点到实际场景,再用真实数据集跑一遍看效果。
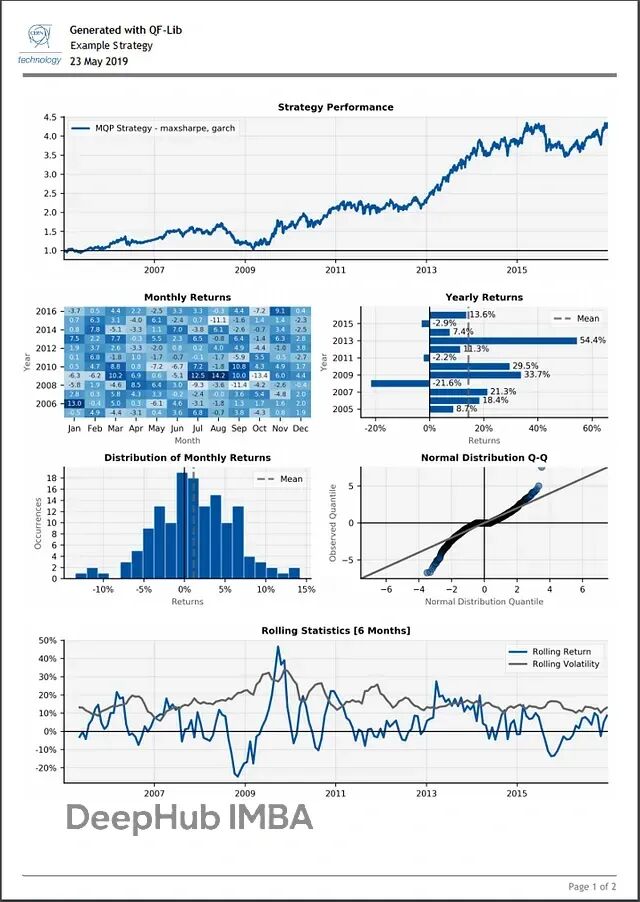
QF-Lib:用一个库搞定Python量化回测和策略开发
QF-Lib(Quantitative Finance Library)是个金融研究和回测工具包。从数据获取到策略模拟、风险评估,再到最后的报告生成,基本能在这一个工具里搞定。
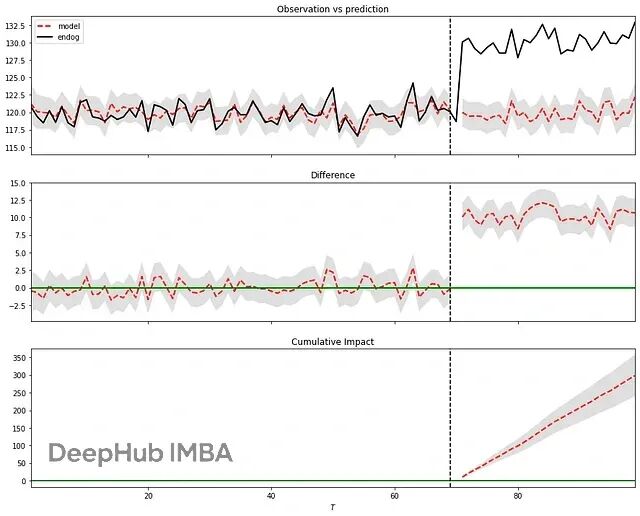
Python因果分析选哪个?六个贝叶斯推断库实测对比(含代码示例)
这篇文章将对比了六个目前社区中最常用的因果推断库:**Bnlearn、Pgmpy、CausalNex、DoWhy、PyAgrum 和 CausalImpact**。
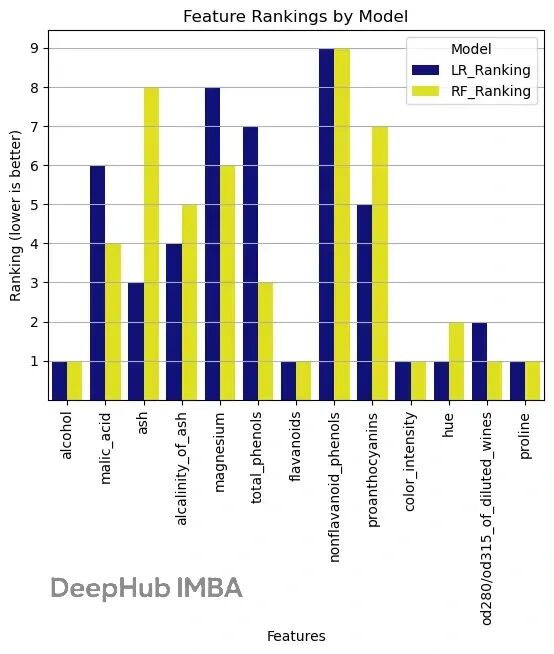
sklearn 特征选择实战:用 RFE 找到最优特征组合
本文会详细介绍RFE 的工作原理,然后用 scikit-learn 跑一个完整的例子。
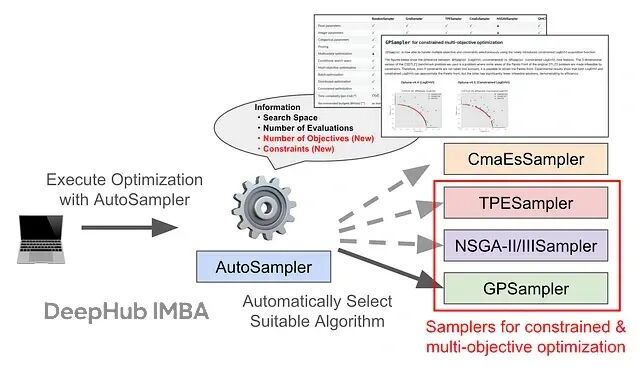
Optuna AutoSampler 更新:让多目标和约束优化不再需要手动选算法
这篇文章会讲清楚新功能怎么用,顺带看看基准测试的表现如何。最新版本其实现在就能用了。