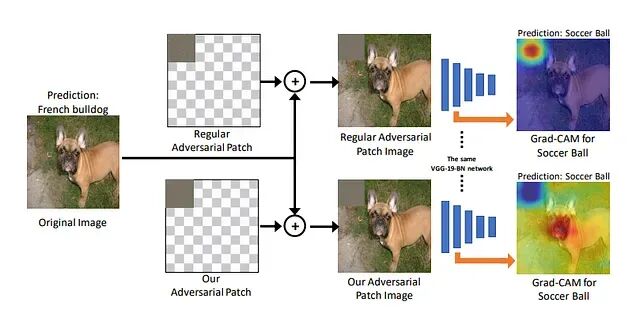
对抗样本:20行Python代码让95%准确率的图像分类器彻底失效
本文会用FGSM(快速梯度符号法)演示如何制作对抗样本,并解释神经网络为何如此脆弱。
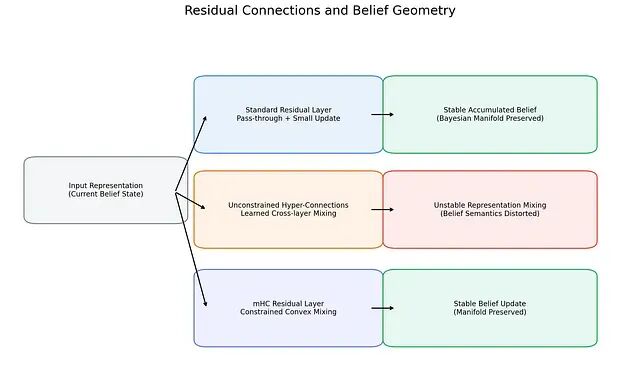
从贝叶斯视角解读Transformer的内部几何:mHC的流形约束与大模型训练稳定性
近期研究揭示了一个有趣的现象:Transformer内部确实在执行贝叶斯推理:只不过不是符号化的方式而是几何化的。
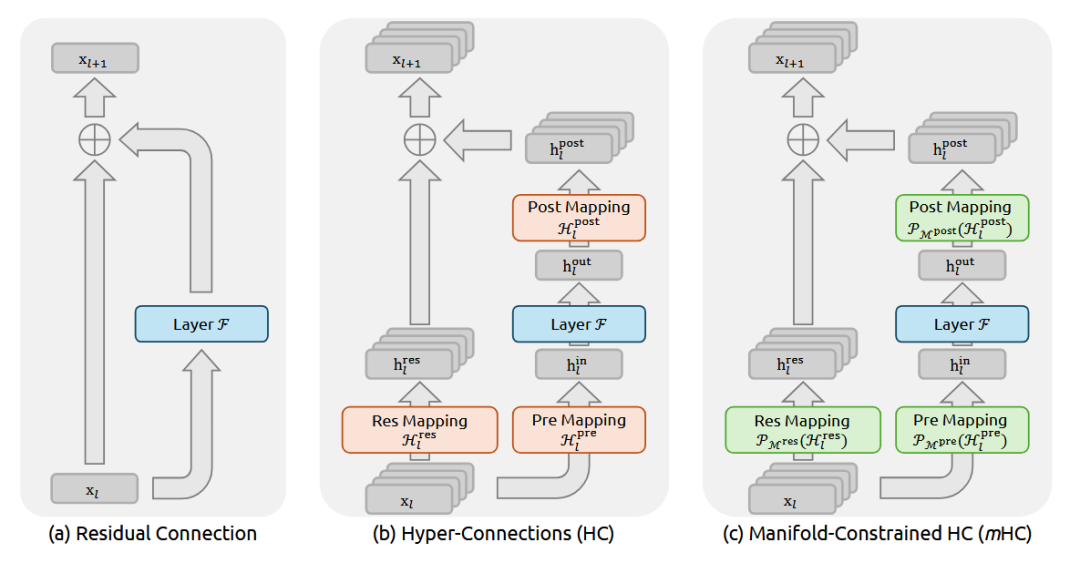
DeepSeek 开年王炸:mHC 架构用流形约束重构 ResNet 残差连接
这回DeepSeek又要对 残差连接(Residual Connection)出手了。
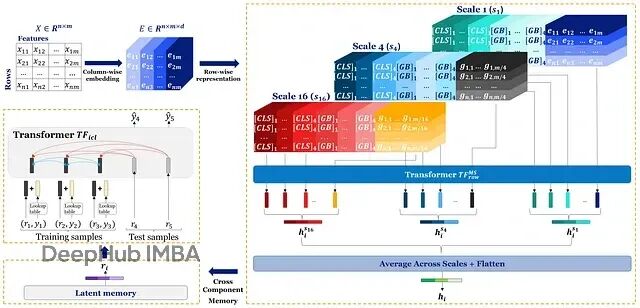
Orion-MSP:深度学习终于在表格数据上超越了XGBoost
Orion-MSP通过多尺度处理捕获不同粒度的特征交互;块稀疏attention把复杂度降到接近线性;Perceiver-style memory实现ICL-safe的双向信息共享。
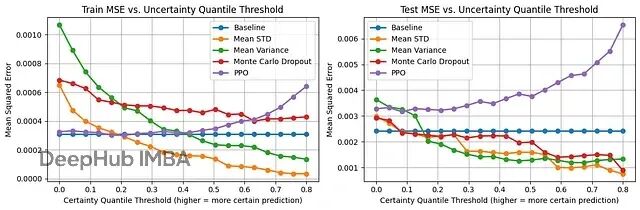
提升回归模型可信度:4种神经网络不确定性估计方法对比与代码实现
神经网络有几种方法可以在给出预测的同时估计不确定性。
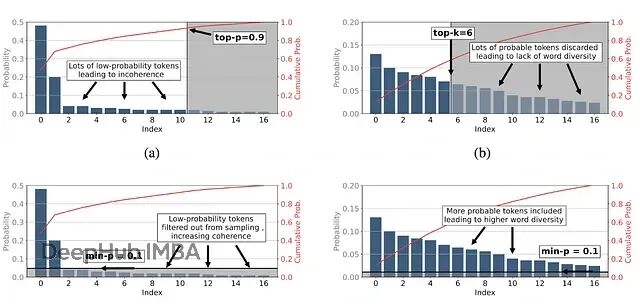
Min-p采样:通过动态调整截断阈值让大模型文本生成兼顾创造力与逻辑性
Min-p 采样的出现为大语言模型文本生成领域带来了新的思路。它通过动态调整采样阈值,让模型能够在不同的上下文中灵活地平衡创造性与连贯性
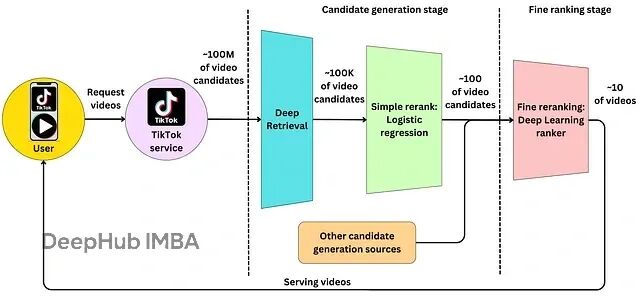
从零构建短视频推荐系统:双塔算法架构解析与代码实现
本文将从技术角度剖析:双塔架构的工作原理、为何在短视频场景下表现卓越,以及如何构建一套类似的推荐系统。
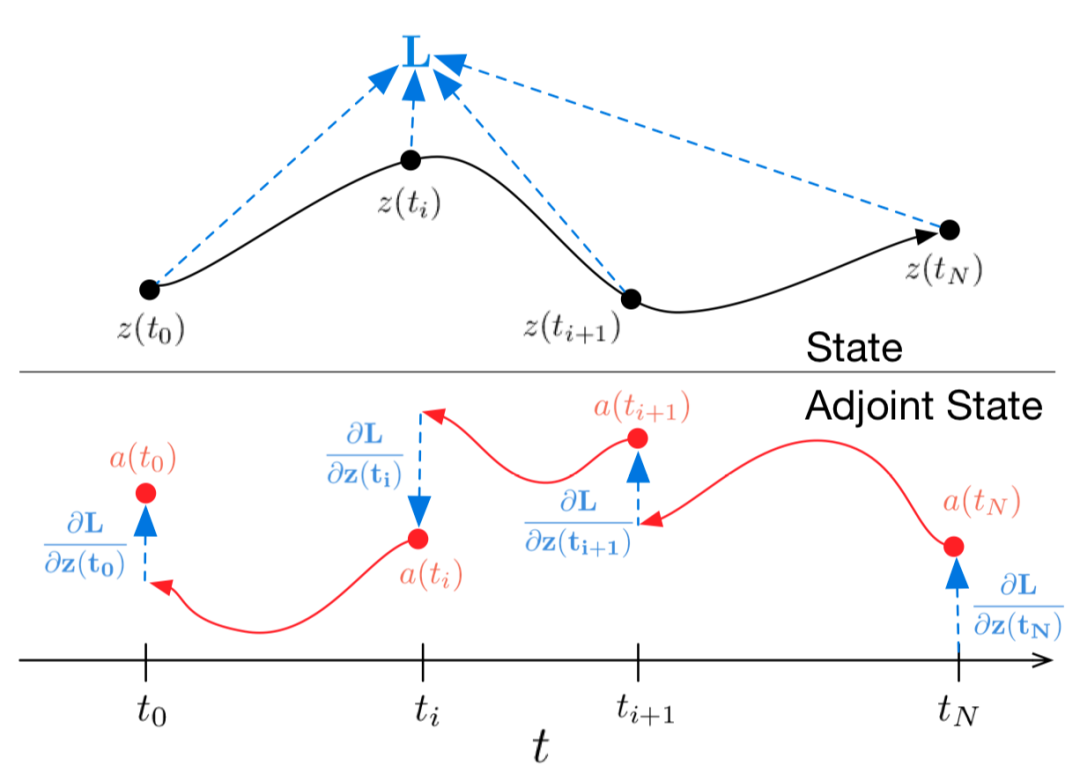
Neural ODE原理与PyTorch实现:深度学习模型的自适应深度调节
文章详细介绍了从基础ODE概念到PyTorch实现的完整流程,并通过捕食者-猎物生态系统案例展示了其在时间序列预测中的应用优势。这种连续化思维为处理物理、生物、金融等领域的动态系统提供了新的建模范式。
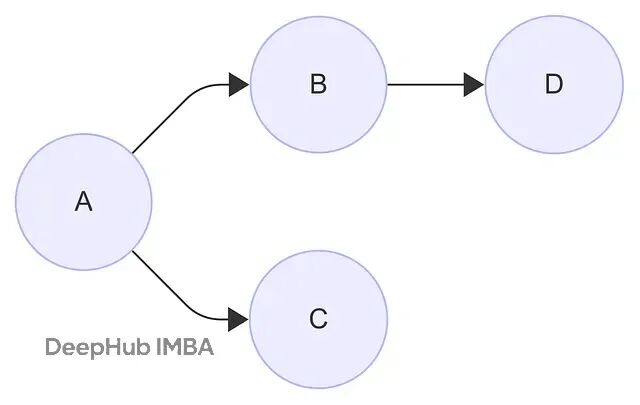
从零开始构建图注意力网络:GAT算法原理与数值实现详解
本文文会详细拆解GAT的工作机制,用一个具体的4节点图例来演示整个计算过程。如果你读过原论文觉得数学公式比较抽象,这里的数值例子应该能让你看清楚GAT到底是怎么运作的。

神经架构搜索NAS详解:三种核心算法原理与Python实战代码
最近好多论文开始将 **神经架构搜索(NAS)** 应用于**大模型**或 **大型语言/视觉语言模型**的设计中。所以我来回顾一下NAS的基础技术。
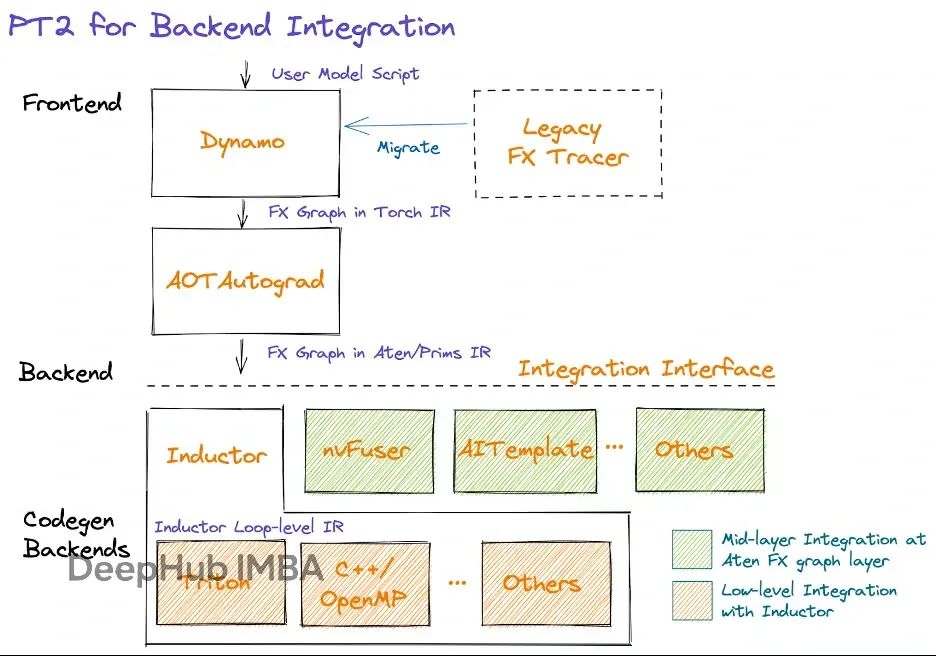
PyTorch 2.0性能优化实战:4种常见代码错误严重拖慢模型
我们将深入探讨图中断(graph breaks)和多图问题对性能的负面影响,并分析PyTorch模型开发中应当避免的常见错误模式。

Dots.ocr:告别复杂多模块架构,1.7B参数单一模型统一处理所有OCR任务
本文将深入分析Dots.ocr的技术架构特点、性能表现以及在实际应用中的价值,探讨这一模型如何在参数效率与处理能力之间找到最佳平衡点。
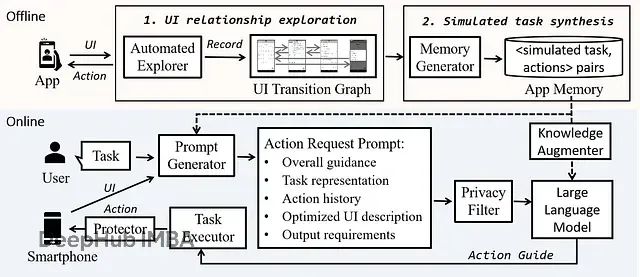
大型动作模型LAM:让企业重复任务实现80%效率提升的AI技术架构与实现方案
本文将深度剖析LAMs的技术架构,详细阐述其核心组件的设计原理、功能实现机制以及在实际业务场景中的应用模式
普通电脑也能跑AI:10个8GB内存的小型本地LLM模型推荐
本文将深入分析如何在本地硬件环境中部署先进的AI模型,并详细介绍当前最具代表性的轻量级模型解决方案。
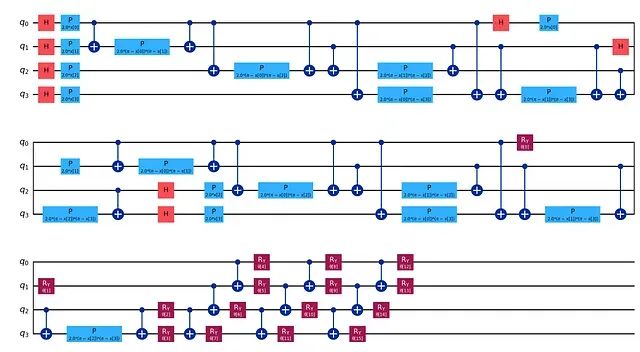
GQNN框架:让Python开发者轻松构建量子神经网络
为降低量子神经网络的研发门槛并提升其实用性,本文介绍一个名为GQNN(Generalized Quantum Neural Network)的Python开发框架。
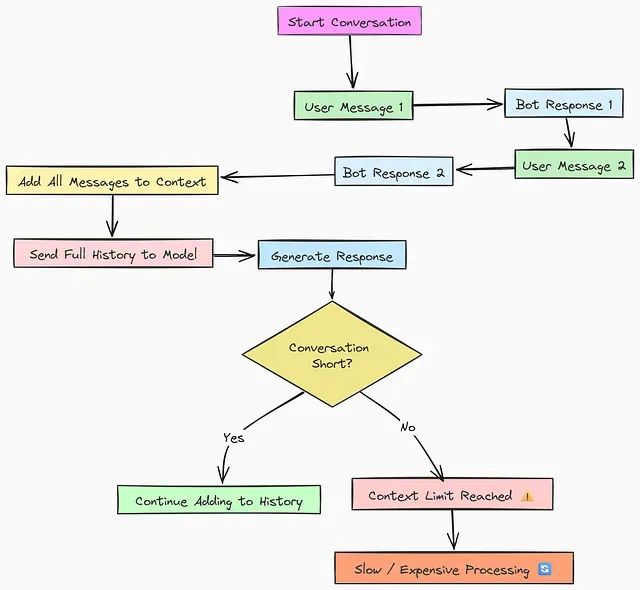
AI代理内存消耗过大?9种优化策略对比分析
本文将深入探讨并实现九种从基础到高级的内存优化技术,涵盖从简单的顺序存储方法到复杂的类操作系统内存管理策略。通过系统性的代码实现和性能评估,我们将分析每种技术的适用场景、优势特点以及潜在限制。
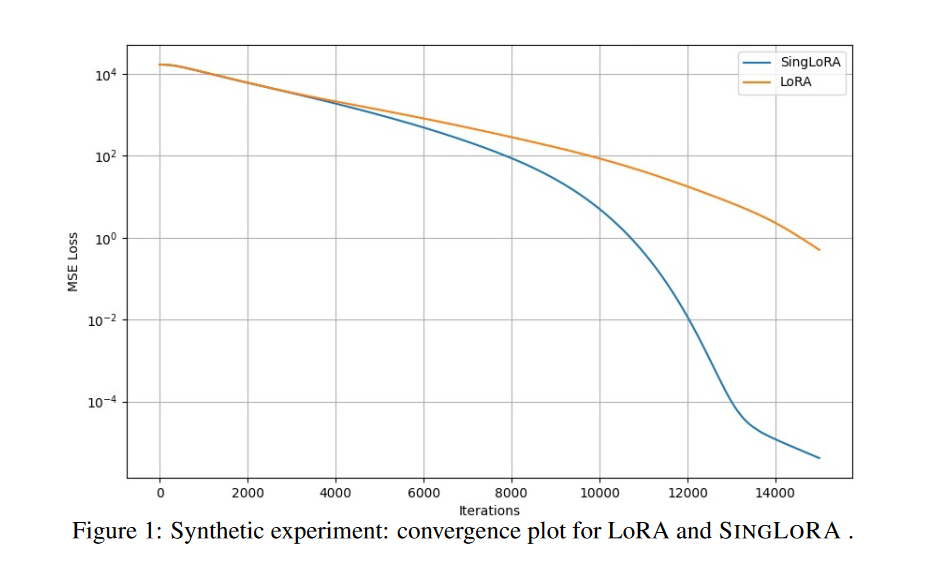
SingLoRA:单矩阵架构减半参数量,让大模型微调更稳定高效
SingLoRA作为一种创新的低秩适应方法,通过摒弃传统的双矩阵架构,采用单矩阵对称更新策略,在简化模型结构的同时显著提升了训练稳定性和参数效率。
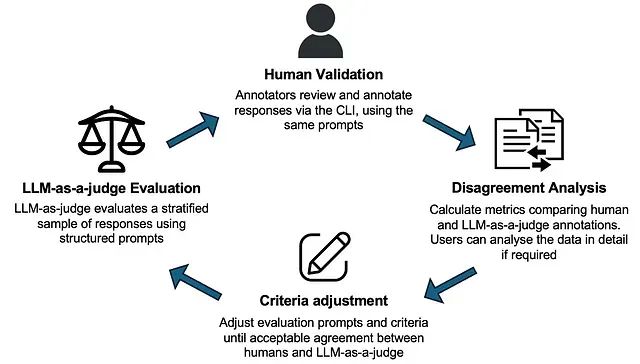
让大语言模型在不知道答案时拒绝回答:KnowOrNot框架防止AI幻觉
KnowOrNot开源框架通过创建可保证的"知识库外"测试场景,评估AI系统是否能够正确识别其知识边界并在信息不足时采取适当的拒绝回答策略。
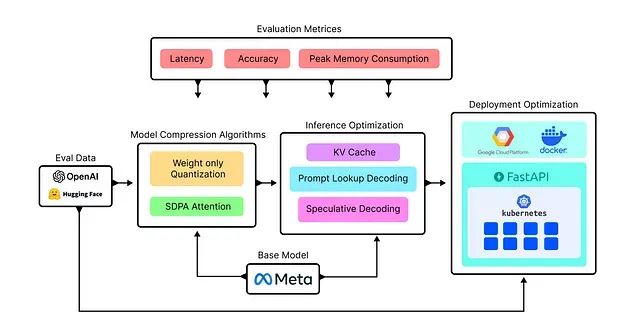
构建高性能LLM推理服务的完整方案:单GPU处理172个查询/秒、10万并发仅需15美元/小时
本文将通过系统性实验不同的优化技术来构建自定义LLaMA模型服务,目标是高效处理约102,000个并行查询请求,并通过对比分析确定最优解决方案。
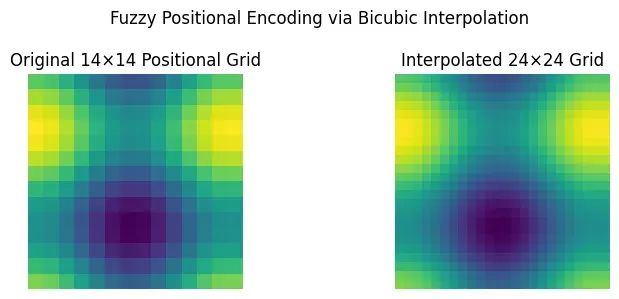
ViTAR:模糊位置编码让视觉Transformer适配任意分辨率图像
ViTAR代表了视觉Transformer技术的重要进步,特别是在处理多样化和高分辨率图像数据的应用场景中表现出显著优势。