这是一篇在2020年发表在ICLR的论文,论文使用图神经网络从稀疏数据中学习连续时间偏微分方程,文章提出的模型主要创新点是允许任意空间和时间离散化,也就是说在求解偏微分划分网格时,网格可以是不均匀的,由于所求解的控制方程是未知的,在表示控制方程时,作者使用了消息传递的图神经网络进行参数化。
在许多系统中偏微分方程至关重要。但是求解大多数偏微分方程长期以来一直是一项艰巨的任务,通常需要复杂的数值求解技巧,尤其是当方程的参数或边界条件部分未知时。
图神经网络 (GNN) 因为在非欧几里得系统建模中具有广泛的适用性,所以可以为求解偏微分方程提供了新颖而令人兴奋的概念。
在本文中,我们将回顾一种使用图神经网络来表示偏微分方程中重要的时间导数分量的方法。
一个常见的偏微分方程定义为,
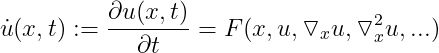
其中系统相对于空间坐标 x 和时间 t 的时间演化取决于其自身及其相对于空间坐标 x 的一阶或更高阶导数。
这种形式的偏微分方程是一大类科学问题的基础,在声波、流体、热扩散等具有传播特性的系统中有着广泛的应用。
[1] 提出使用 GNN 逼近离散点网格的函数 F,将原方程用直线法(MOL)离散化,选取系统域 Ω 中的 N 个节点,因此函数 F 为 在这些空间节点上离散化,可以表示为
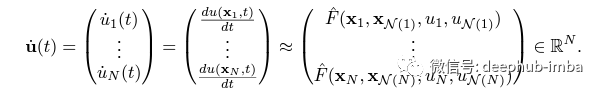
其中 N(i) 是 xi 处相邻节点的一组索引,x*{N(i)} 与 u*{N(i)} 是 N(i) 中节点的位置和状态。
我们将用 G=(V, E) 表示无向图,其中 V 作为顶点集,E 作为边集。为了构建这个图,首先对离散点使用Delaunay三角剖分,如果两个节点在至少一个三角形的同一边上则认为两个节点相邻节点,如下图所示
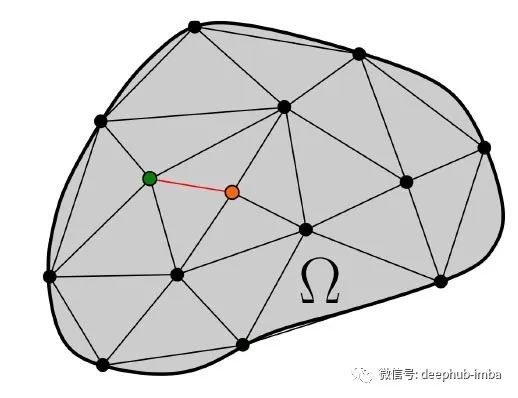
一组点的 Delaunay 三角剖分。绿色和橙色点被认为是邻居,因为它们共享相同的边缘。来源[1]
然后通过使用神经网络的消息传递 (MPNN) 对函数 F 进行建模,通过K个图传播隐藏状态,每层 k 首先为每个节点 i 收集消息,然后更新相应的节点状态,
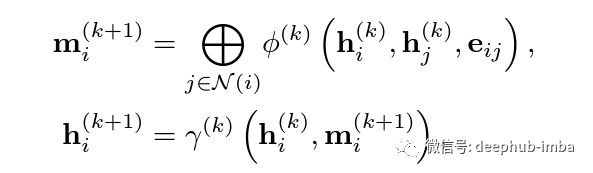
其中φ、γ是DNN参数化的可微函数,
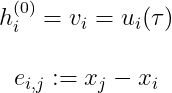
然后用最后一层图形来计算PDE,
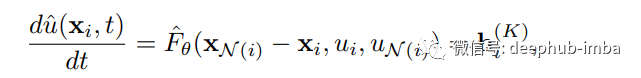
为了监督模型的学习,使用均方误差观测状态和估计状态之间的差异。
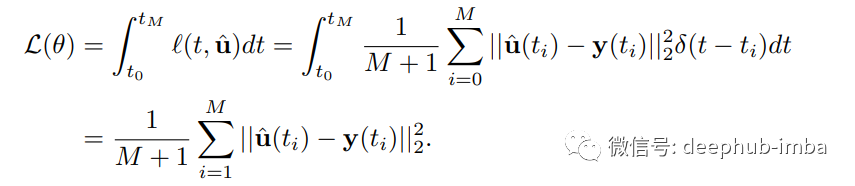
与数据时间间隔较宽的纯离散时间模型相比,这种方法的优势在于它可以在连续时间预测系统的状态,同时在离散时间学习系统的状态。
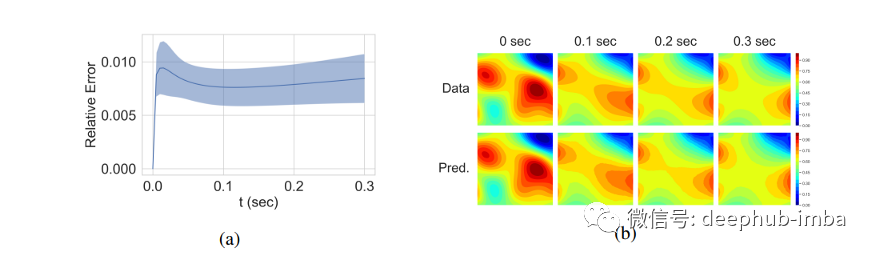
a)热传导方程的相对测试误差。b)真实和学习过的系统动力学。来源[1]
这种进化机制在数学上由偏微分方程描述,图神经网络将这些机制抽象为节点(或边)之间的信息流。论文中提到图神经网络将进一步推动科学研究和社会经济,因为它们与描述自然界和人类社会中广泛存在的非欧几里得数据或系统的自然结构相关性。
论文信息:
1.Valerii Iakovlev, et. al., “Learning Continuous-time PDEs From Sparse Data with Graph Neural Networks”, arXiv:2006.08956.
本文作者:Madali Nabil