似然函数总结
似然函数总结
SPSS学习 相关性分析
进行相关分析双变量相关 计算变量之间皮尔逊相关系数(直接解读) 肯德尔(需要计算偏相关性)斯皮尔曼(需要通过`*`与`**`的大小进行判断)一. 分析花瓣长、花枝长与花萼长两两相关性关系采用皮尔逊 双尾检验显著性检验 双尾(双侧检验) 以0.01为检验标准 单尾(单侧检验) 以0.05为检验标准数据
【可乐荐书】人工智能数学基础
凡事都要打好基础，才能稳定向前。数学知识与数学思维是学习人工智能的基石，只有基础牢固，基石稳定，人工智能技术这座恢弘大厦才能永不倾覆。不掌握数学知识，就无法理解算法的内在逻辑，“照葫芦画瓢”只能应付一时，想要在行业中立足，掌握技术原理是重中之重。《人工智能数学基础》一书以零基础讲解为宗旨，面向学习数
概率统计笔记：二维随机变量及其联合概率分布
联合分布函数
置信椭圆（误差椭圆）详解
对置信椭圆，主成分分析的详细介绍，并附以Matlab绘图脚本
贝叶斯分类器
慢慢地将贝叶斯公式全部都推导一遍，都好好的研究透彻，全部将其搞定都行啦的样子与打算。
点云配准--gicp原理与其在pcl中的使用
在概率模型中假设存在配准中两个点集, A^={ai^}\hat{A}=\left\{\hat{a_{i}}\right\}A^={ai^} and B^={bi^}\hat{B}=\left\{\hat{b_{i}}\right\}B^={bi^},并且假设 AAA and BBB 分别服从
电子科技大学人工智能期末复习笔记（四）：概率与贝叶斯网络
本复习笔记基于李晶晶老师的课堂PPT与复习大纲，供自己期末复习与学弟学妹参考用。 首先明确，P(W | dry)是一个概率分布，而不是一个概率值。不能写成 P(W | dry)=....①求联合概率分布P(D,W);②求边缘概率分布P(D);③求条件概率分布P(W | D).P(W | dry
R数据分析：临床预测模型中校准曲线和DCA曲线的意义与做法
之前给大家写过一个临床预测模型：R数据分析：跟随top期刊手把手教你做一个临床预测模型，里面其实都是比较基础的模型判别能力discrimination的一些指标，那么今天就再进一步，给大家分享一些和临床决策实际相关的指标，主要是校准calibration和决策曲线Decision curve ana
R语言-dnorm-pnorm-qnorm-rnorm的区别
R语言 dnorm, pnorm, qnorm, rnorm的区别前言dnorm, pnorm, qnorm, rnorm 是R语言中常用的正态分布函数. norm 指的是正态分布(也可以叫高斯分布(normal distribution)), R语言中也有其他不同的分布操作也都类似. p q d
机器学习基础 HMM模型（隐马尔科夫）
在机器学习算法中，马尔可夫链(Markov chain)是个很重要的概念。马尔可夫链（Markov chain），又称离散时间马尔可夫链（discrete-time Markov chain），因俄国数学家安德烈·马尔可夫（俄语：Андрей Андреевич Марков）得名。马尔科夫链即为状
协方差矩阵与相关系数矩阵
本篇博客主要介绍一下方差、协方差及相关系数的相关知识，进而引入了协方差矩阵与相关系数矩阵，并结合相关实例进行说明。
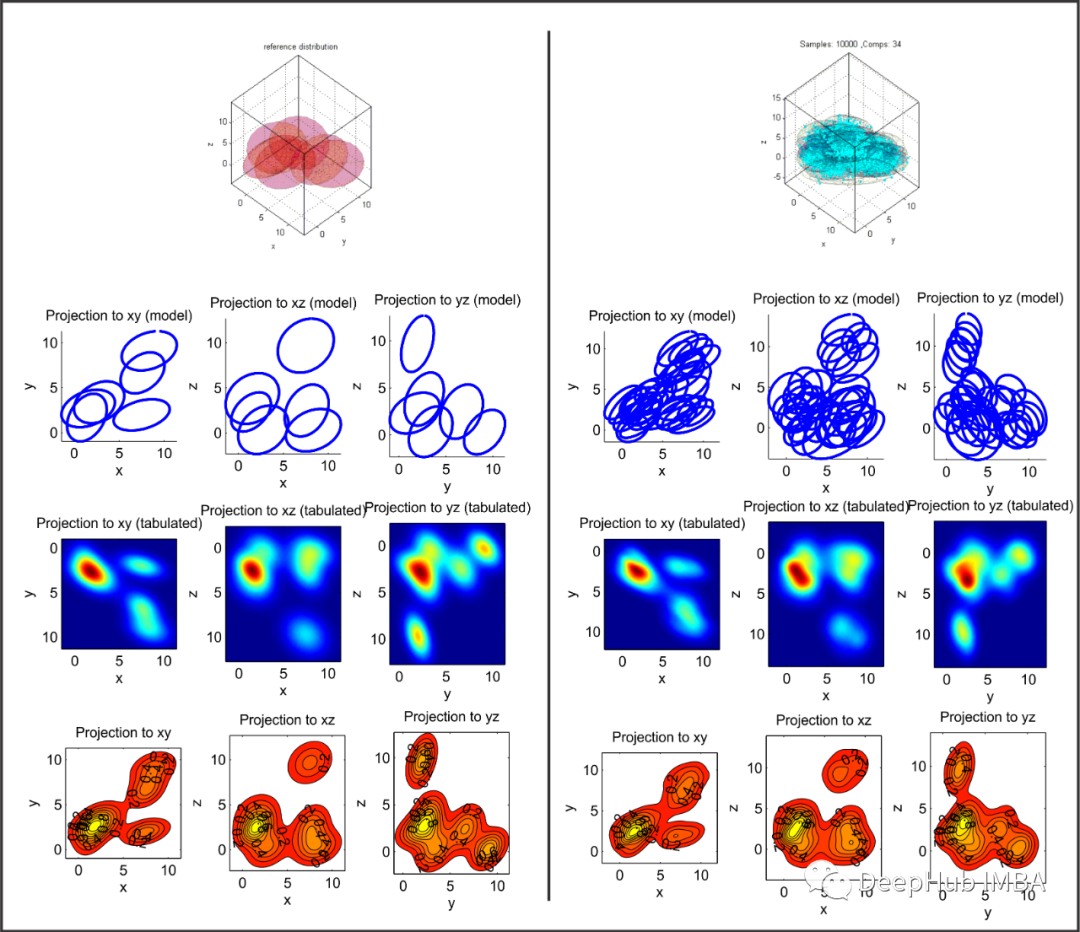
非参数检验方法，核密度估计简介
核密度估计（Kernel Density Estimation，简称KDE）是一种非参数统计方法，用于估计数据样本背后的概率密度函数
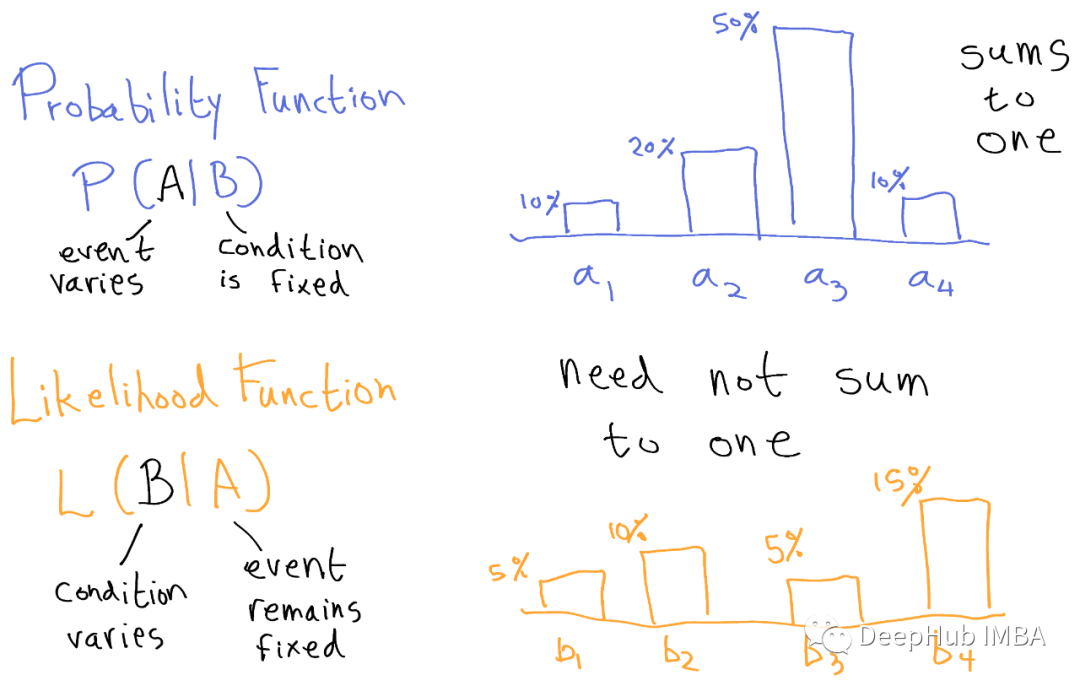
概率和似然
在日常生活中，我们经常使用这些术语。但是在统计学和机器学习上下文中使用时，有一个本质的区别。本文将用理论和例子来解释概率和似然之间的关键区别。
概率还不会的快看过来《统计学习方法》——第四章、朴素贝叶斯法
作者简介：整个建筑最重要的是地基，地基不稳，地动山摇。而学技术更要扎稳基础，关注我，带你稳扎每一板块邻域的基础。博客主页：啊四战斗霸的博客专栏：《统计学习方法》第二版——个人笔记创作不易，走过路过别忘了三连击了哟！！！关注作者，不仅幸运爆棚，未来更可期！！！***有代码，就有注释！！！Triple
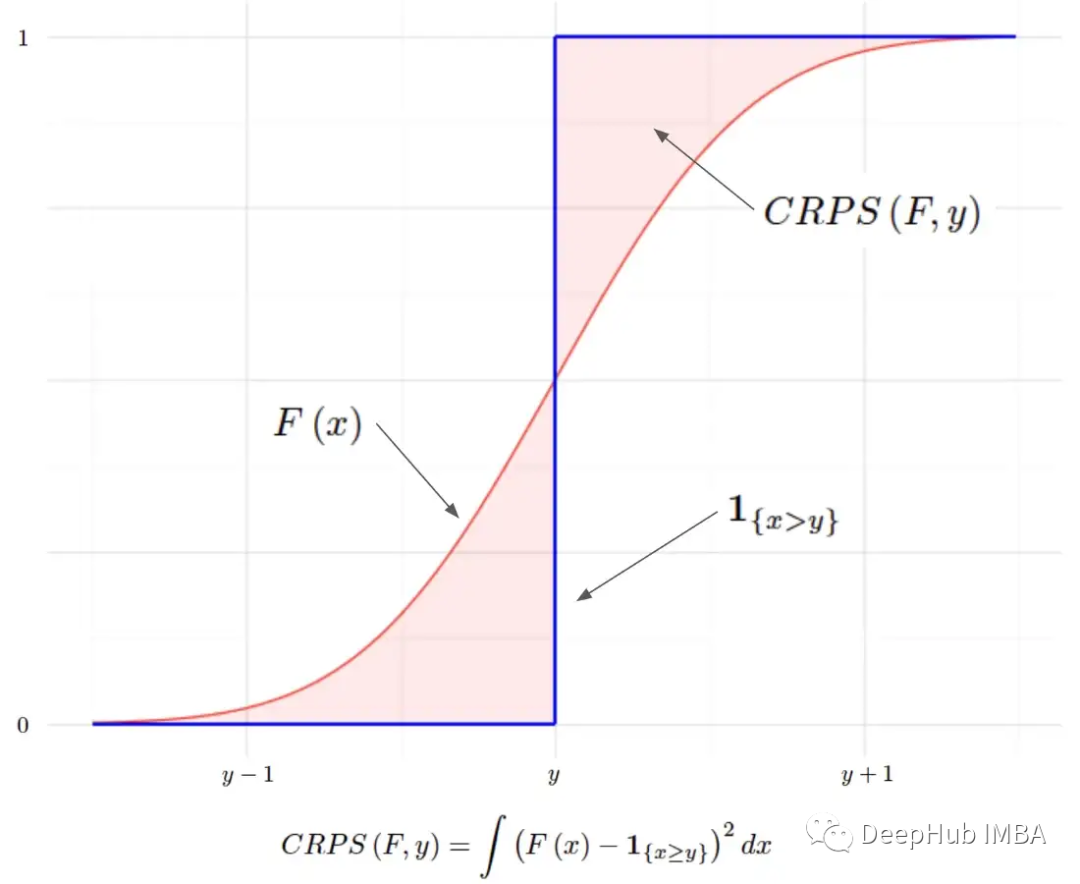
CRPS：贝叶斯机器学习模型的评分函数
连续分级概率评分（Continuous Ranked Probability Score, CRPS）或“连续概率排位分数”是一个函数或统计量，可以将分布预测与真实值进行比较。
R语言-dnorm-pnorm-qnorm-rnorm的区别
R语言 dnorm, pnorm, qnorm, rnorm的区别前言dnorm, pnorm, qnorm, rnorm 是R语言中常用的正态分布函数. norm 指的是正态分布(也可以叫高斯分布(normal distribution)), R语言中也有其他不同的分布操作也都类似. p q d
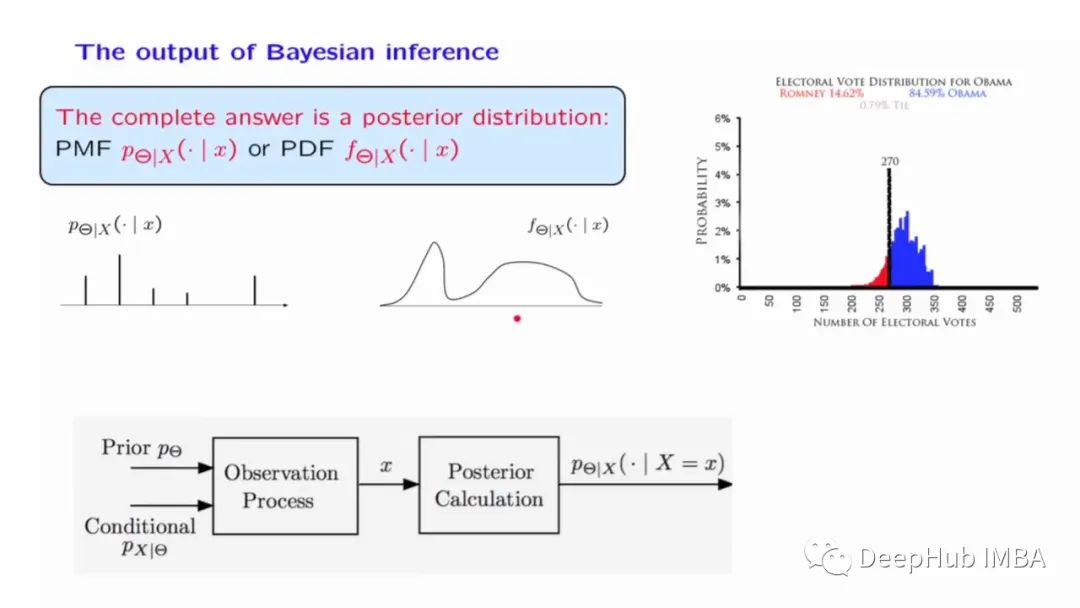
贝叶斯推理三种方法：MCMC 、HMC和SBI
本文将阐明为什么贝叶斯方法不仅在逻辑上是合理的，而且使用起来也很简单。这里将以三种不同的方式实现相同的推理问题。
我们能从后验分布中学到什么?贝叶斯后验的频率解释
假设我们从未知分布 q 中观察到 N 个独立且同分布的 (iid) 样本 X = (x1, ... , xN)。统计学中的一个典型问题是“样本集 X 能告诉我们关于分布 q 的什么信息？”。
哈工大2022机器学习实验二：逻辑回归
逻辑回归，又意译为对率回归，虽然它的名字中带“回归”，但它是一个分类模型。它的基本思想是直接估计条件概率P(Y|X)的表达式，即给定样本X=x，其属于类别Y的概率。
