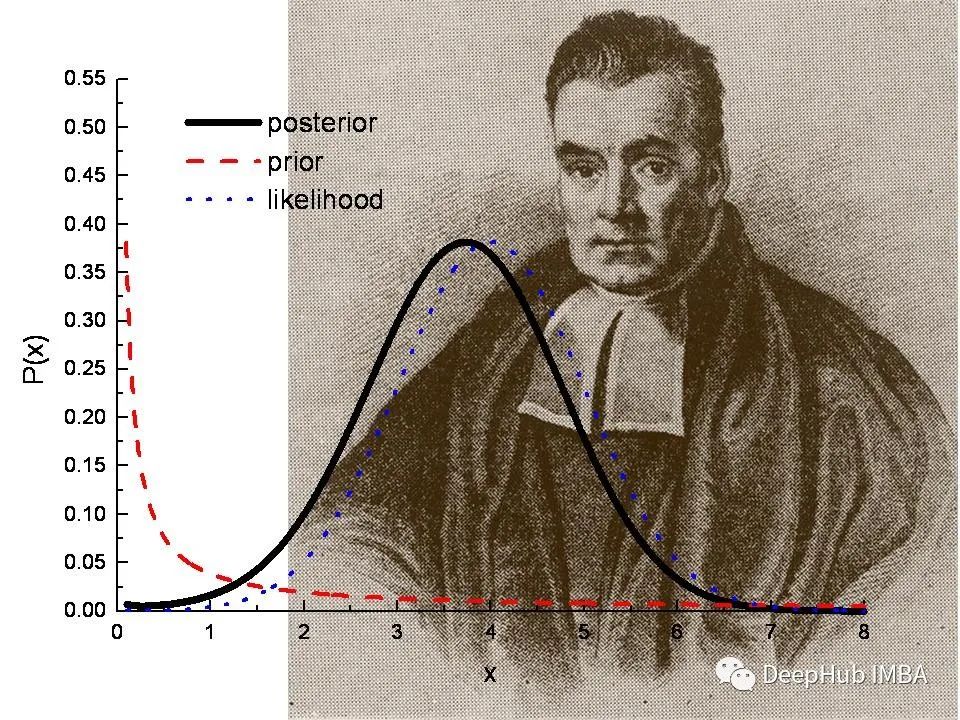
我们能从后验分布中学到什么?贝叶斯后验的频率解释
假设我们从未知分布 q 中观察到 N 个独立且同分布的 (iid) 样本 X = (x1, ... , xN)。统计学中的一个典型问题是“样本集 X 能告诉我们关于分布 q 的什么信息?”。
哈工大2022机器学习实验二:逻辑回归
逻辑回归,又意译为对率回归,虽然它的名字中带“回归”,但它是一个分类模型。它的基本思想是直接估计条件概率P(Y|X)的表达式,即给定样本X=x,其属于类别Y的概率。
将特征转换为正态分布的一种方法示例
正态(高斯)分布在机器学习中起着核心作用,线性回归模型中要假设随机误差等方差并且服从正态分布,如果变量服从正态分布,那么更容易建立理论结果。
以数据为中心和模型为中心的AI是贝叶斯论和频率论的另一种变体吗?
在这篇文章中,我将对这两种方法提供一个新的视角。我将从统计的角度来看它们,看看它是否可以阐明哪种方法更好以及在什么情况下更好。

联合概率和条件概率的区别和联系
本文解释联合概率和条件概率之间区别和联系
【R语言数据科学】(十二):有趣的概率学(上)
你真的了解概率吗?在机会游戏中,概率有一个非常直观的定义。例如,我们知道一对骰子出现七的机会是六分之一。但是,现实情况中,概率并不是一个确定的值。在如今,我们常常喜欢用概率来解释现实问题。例如,明天下雨的概率、被鲨鱼咬的概率、癌症的概率等等。知道如何计算概率会让你在机会游戏中占据优势,纵观历史,许多

14个面试中常见的概率问题
在任何数据科学面试中,基本上都会问道一些有关概率的问题。 这在本文中我总结了一些相关的问题供大家参考。
独孤九剑第五式-朴素贝叶斯模型
💐文章适合于所有的相关人士进行学习💐🍀各位看官看完了之后不要立刻转身呀🍀🌿期待三连关注小小博主加收藏🌿🍃小小博主回关快 会给你意想不到的惊喜呀🍃各位老板动动小手给小弟点赞收藏一下,多多支持是我更新得动力!!!文章目录🏰前言🏰朴素贝叶斯模型理论讲解⛺️模型思想⛺️贝叶斯理论讲解⛺️
概率还不会的快看过来《统计学习方法》——第四章、朴素贝叶斯法
作者简介:整个建筑最重要的是地基,地基不稳,地动山摇。而学技术更要扎稳基础,关注我,带你稳扎每一板块邻域的基础。博客主页:啊四战斗霸的博客专栏:《统计学习方法》第二版——个人笔记创作不易,走过路过别忘了三连击了哟!!!关注作者,不仅幸运爆棚,未来更可期!!!***有代码,就有注释!!!Triple
程序员的数学【AIoT阶段二】
不论你是一位刚入程序员门槛的大学生,亦或者是想系统学习程序员数学,这篇文章绝对可以满足你的需求,本篇博客涉及所有程序员数学的必备知识,是 【AIoT阶段二】的内容:算法数学基础,关于所有AIoT的详细介绍,详见博客:AIoT(人工智能+物联网)知识总结+实战项目,先来简单介绍通过本文,你可以学到什么
程序员的数学【概率论】
本文其实值属于:程序员的数学【AIoT阶段二】 (尚未更新)的一部分内容,本篇把这部分内容单独截取出来,方便大家的观看,本文介绍 概率论,本文涵盖了一些计算的问题并使用代码进行了实现,安装代码运行环境见博客:最详细的Anaconda Installers 的安装【numpy,jupyter】(图+文
NumPy快速入门(四)——随机抽样与通用函数
目录一、随机抽样(np.random模块)1.1 np.random.random()1.2 np.random.uniform()1.3 np.random.randn()1.4 np.random.randint()1.5 np.random.rand()1.6 np.random.normal
Jensen不等式
引言 概率不等式是概率论和数理统计的理论研究中的重要工具,对于概率极限理论和统计大样本理论,几乎所有重要结果的论证是借助于概率不等式的巧妙应用,Jensen\mathrm{Jensen}Jensen不等式和证明,并应用其带来解决一些相关问题。Jensen\mathrm{Jensen}Jensen不等
机器学习基础知识之概率论的多维随机变量及其分布
机器学习基础知识之概率论的多维随机变量及其分布文章目录机器学习基础知识之概率论的多维随机变量及其分布一、多维随机变量及其联合分布1、多维随机变量一、多维随机变量及其联合分布1、多维随机变量...
矩量母函数介绍
1 矩量母函数 矩量母函数又称矩母函数(Moment Generating Function)又称动差生成函数,是一种构造函数,其定义为:随机变量XXX是连续型随机变量时,其矩量母函数为:MX(t)=E(etX)=∫−∞+∞etxf(x)dxM_X(t)=\mathrm{E}(e^{tX})=\in
条件期望求解快速排序算法复杂度
1 条件期望定义1(条件期望):给定随机变量XXX和YYY,则有如下条件期望E[X]=E[E[X∣Y]]\mathrm{E}[X]=\mathrm{E}\left[\mathrm{E}[X|Y]\right]E[X]=E[E[X∣Y]]如果YYY是离散随机变量,则有E[X]=∑yE[X∣Y=y]P{
python在球面上随机生成均匀点最简单的方法
python在球面上随机生成均匀点最简单的方法
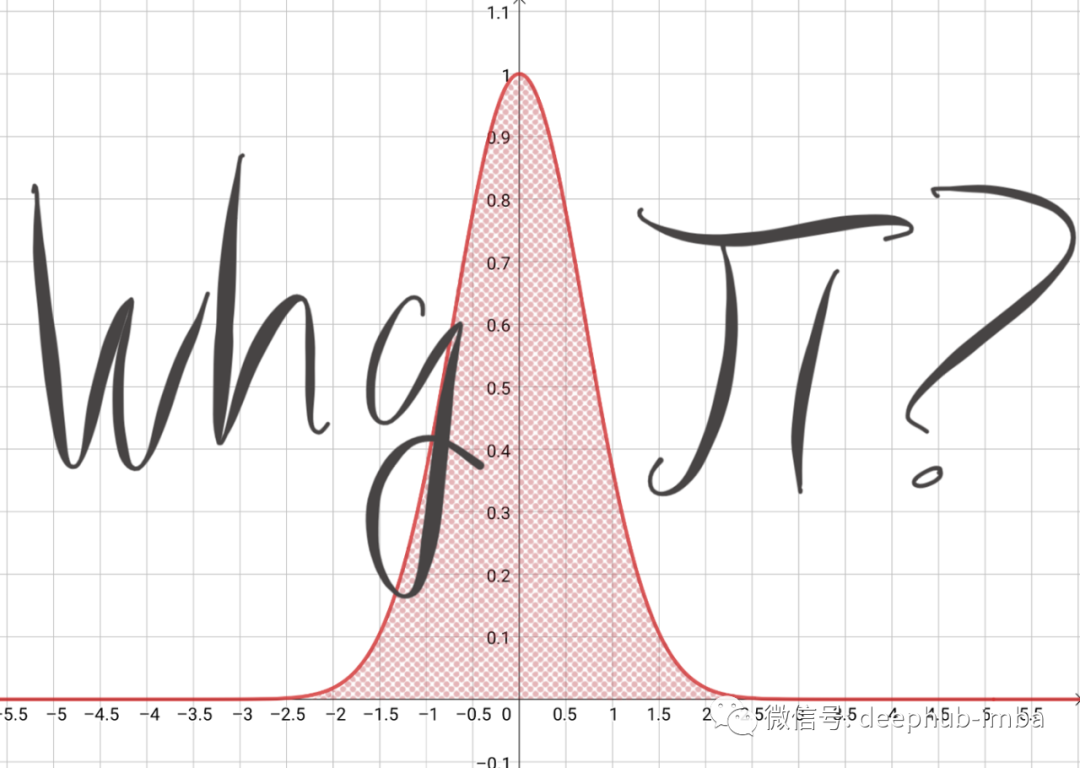
为什么 Pi 会出现在正态分布的方程中?
本篇文章将介绍钟形曲线是如何形成的,以及π为什么会出现在一个看似与它无关的曲线的公式中。