文章目录
总结：gicp引入了概率信息（使用协方差阵），提出了icp的统一模型，既可以解释点到点和点到面的icp，也在新模型理论的基础上，提出了一种面到面的icp。
论文原文：《Generalized-ICP》
gicp统一模型（Generalized-ICP）
在概率模型中假设存在配准中两个点集,
A^={ai^}\hat{A}=\left\{\hat{a_{i}}\right\}A^={ai^} andB^={bi^}\hat{B}=\left\{\hat{b_{i}}\right\}B^={bi^},并且假设AAA andBBB 分别服从ai∼N(ai^,CiA)a_{i} \sim \mathcal{N}\left(\hat{a_{i}}, C_{i}^{A}\right)ai∼N(ai^,CiA)andbi∼N(b^i,CiB)b_{i} \sim \mathcal{N}\left(\hat{b}_{i}, C_{i}^{B}\right)bi∼N(b^i,CiB)正态分布.{CiA}\left\{C_{i}^{A}\right\}{CiA} and{CiB}\left\{C_{i}^{B}\right\}{CiB} 分别是点对应的协方差阵. 我们假设以及匹配完成，假设变换矩阵为T∗\mathbf{T}^{*}T∗, 因此：b^i=T∗a^i(1)\hat{b}_{i}=\mathbf{T}^{*} \hat{a}_{i}\tag{1}b^i=T∗a^i(1)
对于变换矩阵,
T\mathbf{T}T , 定义误差量di(T)=bi−Taid_{i}^{(\mathbf{T})}= b_{i}-\mathbf{T} a_{i}di(T)=bi−Tai, 因为假设aia_{i}ai andbib_{i}bi 服从正态分布（NDT也是假设服从正态分布）， 因此di(T∗)d_{i}^{\left(\mathrm{T}^{*}\right)}di(T∗) 也服从正态分布：di(T∗)∼N(b^i−(T∗)a^i,CiB+(T∗)CiA(T∗)T)=N(0,CiB+(T∗)CiA(T∗)T)(2)\begin{aligned} d_{i}^{\left(\mathbf{T}^{*}\right)} & \sim \mathcal{N}\left(\hat{b}_{i}-\left(\mathbf{T}^{*}\right) \hat{a}_{i}, C_{i}^{B}+\left(\mathbf{T}^{*}\right) C_{i}^{A}\left(\mathbf{T}^{*}\right)^{T}\right) \\ &=\mathcal{N}\left(0, C_{i}^{B}+\left(\mathbf{T}^{*}\right) C_{i}^{A}\left(\mathbf{T}^{*}\right)^{T}\right) \end{aligned}\tag{2}di(T∗)∼N(b^i−(T∗)a^i,CiB+(T∗)CiA(T∗)T)=N(0,CiB+(T∗)CiA(T∗)T)(2)
使用最大似然估计（ MLE）计算
T\mathbf{T}T ：T=argmaxT∏ip(di(T))=argmaxT∑ilog(p(di(T)))(3)\mathbf{T}=\underset{\mathbf{T}}{\operatorname{argmax}} \prod_{i} p\left(d_{i}^{(\mathrm{T})}\right)=\underset{\mathbf{T}}{\operatorname{argmax}} \sum_{i} \log \left(p\left(d_{i}^{(\mathrm{T})}\right)\right)\tag{3}T=Targmaxi∏p(di(T))=Targmaxi∑log(p(di(T)))(3)
进一步简化为：（这里从最大似然估计推导，具体过程需要研究）
T=argminT∑idi(T)T(CiB+TCiATT)−1di(T)(4)\mathbf{T}=\underset{\mathrm{T}}{\operatorname{argmin}} \sum_{i} d_{i}^{(\mathbf{T})^{T}}\left(C_{i}^{B}+\mathbf{T} C_{i}^{A} \mathbf{T}^{T}\right)^{-1} d_{i}^{(\mathbf{T})}\tag{4}T=Targmini∑di(T)T(CiB+TCiATT)−1di(T)(4)
当：
CiB=ICiA=0(5)C_{i}^{B} = I \\ C_{i}^{A} = 0\tag{5}CiB=ICiA=0(5)
就得到标准ICP:
T=argminT∑idi(T)Tdi(T)=argminT∑i∥di(T)∥2(6)\begin{aligned} \mathbf{T} &=\underset{\mathbf{T}}{\operatorname{argmin}} \sum_{i} d_{i}^{(\mathrm{T})^{T}} d_{i}^{(\mathrm{T})} \\ &=\underset{\mathbf{T}}{\operatorname{argmin}} \sum_{i}\left\|d_{i}^{(\mathrm{T})}\right\|^{2} \end{aligned}\tag{6}T=Targmini∑di(T)Tdi(T)=Targmini∑∥∥∥di(T)∥∥∥2(6)
当：
CiB=Pi−1CiA=0(7)\begin{aligned} C_{i}^{B} &=\mathbf{P}_{\mathbf{i}}^{-1} \\ C_{i}^{A} &=0 \end{aligned}\tag{7}CiBCiA=Pi−1=0(7)
得到点到面的ICP:
T=argminT{∑i∥Pi⋅di∥2}(8)\mathbf{T}=\underset{\mathbf{T}}{\operatorname{argmin}}\left\{\sum_{i}\left\|\mathbf{P}_{\mathbf{i}} \cdot d_{i}\right\|^{2}\right\}\tag{8}T=Targmin{i∑∥Pi⋅di∥2}(8)
plane to plane ICP(gicp：相对于点到点和点到面加入概率模型（协方差阵）)
点到平面算法的做法是，假设点云具有平面特征，这意味着在3D空间处理采样2D流形。
由于现实世界的曲面至少是分段可微的，我们可以假设我们的数据集是局部平面的。此外，由于我们从两个不同的角度对流形进行采样，因此通常不会对完全相同的点进行采样（即，对应关系永远不会是精确的）。
本质上，每个测量点仅提供沿其曲面法线的约束。为了对这种结构进行建模，我们考虑每个采样点沿其局部平面以高协方差分布，而在曲面法线方向（垂直于平面方向）以极低协方差分布（即点云分布在局部平面上）。假设局部拟合平面上某一点的法向量e1是沿X轴的,链接1，则该点协方差矩阵变为：
(ϵ00010001)(9)\left(\begin{array}{lll} \epsilon & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right)\tag{9}⎝⎛ϵ00010001⎠⎞(9)ϵ\epsilonϵ是沿着法线方向极小的常数。
因为实际上法向量并不一定是沿x轴方向，所以需要进行坐标转换。假设
bi,aib_i,a_ibi,ai对应的法向量分别为ui,viu_i,v_iui,vi,则它们对应的协方差阵为：CiB=Rμi⋅(ϵ00010001)⋅RμiTCiA=Rνi⋅(ϵ00010001)⋅RνiT\begin{array}{l} C_{i}^{B}=\mathbf{R}_{\mu_{i}} \cdot\left(\begin{array}{ccc} \epsilon & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) \cdot \mathbf{R}_{\mu_{i}}^{T} \\ C_{i}^{A}=\mathbf{R}_{\nu_{i}} \cdot\left(\begin{array}{ccc} \epsilon & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) \cdot \mathbf{R}_{\nu_{i}}^{T} \end{array}CiB=Rμi⋅⎝⎛ϵ00010001⎠⎞⋅RμiTCiA=Rνi⋅⎝⎛ϵ00010001⎠⎞⋅RνiTRνi\mathbf{R}_{\nu_{i}}Rνi为e1到vi旋转矩阵。
上述协方差计算过程可以表述如下图,链接2：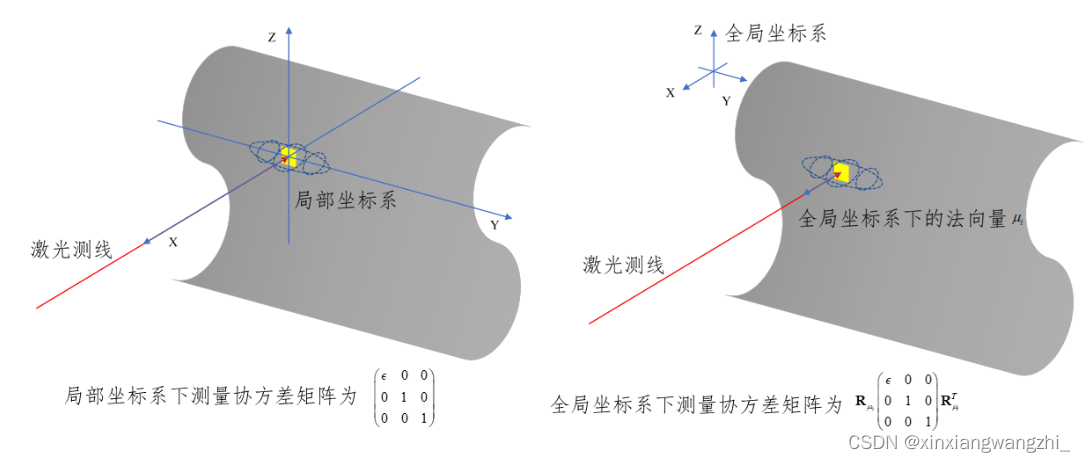
确定协方差阵后利用公式（4）即为plane to plane ICP或者叫GICP。
这里其实就是怎么确定协方差阵。
显然可以通过pca计算协方差阵（代替上述求解过程）：
C=1N⋅∑i=1N⋅(pi−pˉ)⋅(pi−pˉ)TC=\frac{1}{N} \cdot \sum_{i=1}^{N} \cdot\left(p_{i}-\bar{p}\right) \cdot\left(p_{i}-\bar{p}\right)^{T}C=N1⋅i=1∑N⋅(pi−pˉ)⋅(pi−pˉ)T
pca求解时要注意公式（4）对协方差有个求逆过程，需要注意当协方差阵奇异时，用微小量替代0值（类似NDT中处理方式）。
PCL中GICP代码应用
#include<pcl/point_types.h>#include<pcl/point_cloud.h>#include<pcl/registration/gicp.h>intgicp(const pcl::PointCloud<pcl::PointXYZ>::Ptr src_cloud,const pcl::PointCloud<pcl::PointXYZ>::Ptr tgt_cloud,pcl::PointCloud<pcl::PointXYZ>::Ptr transformed_source){pcl::GeneralizedIterativeClosestPoint<pcl::PointXYZ, pcl::PointXYZ> gicp;gicp.setInputSource(src_cloud);gicp.setInputTarget(tgt_cloud);//gicp.setMaximumIterations(max_iter);gicp.align(*transformed_source);return1;}
本文转载自: https://blog.csdn.net/xinxiangwangzhi_/article/details/125236953
版权归原作者 xinxiangwangzhi_ 所有， 如有侵权，请联系我们删除。
版权归原作者 xinxiangwangzhi_ 所有， 如有侵权，请联系我们删除。