作者简介：整个建筑最重要的是地基，地基不稳，地动山摇。而学技术更要扎稳基础，关注我，带你稳扎每一板块邻域的基础。
博客主页：七归的博客
收录专栏：《统计学习方法》第二版——个人笔记
南来的北往的，走过路过千万别错过，错过本篇，“精彩”可能与您失之交臂 la
Triple attack(三连击):Comment,Like and Collect—>Attention
文章目录
简介
- 朴素贝叶斯法是基于贝叶斯定理和特征条件独立假设的分类方法。对于给定训练数据集，首先基于特征条件独立性假设学习输入和输出的联合概率分布；然后基于此模型，对给定的输入新实例x，利用贝叶斯定理求出最大的后验概率输出y。
- 朴素贝叶斯不会直接学习输入和输出的联合概率分布，而是通过学习类的先验概率和类条件概率来完成。
- 朴素贝叶斯法包括朴素贝叶斯法的学习与分类、朴素贝叶斯法的参数估计算法。
1、全概率公式与贝叶斯定理
- 概率：事件X发生的可能性就被称为X发生的概率，用~P(X)来表示
- 先验概率：通过经验来判断事件发生的概率，或当这个概率分布在进行现场试验或者抽样前就已确定
- 后验概率：在已知结果的前提下，推测其造成的原因的概率
- 条件概率：当事件Y已经发生的时候，事件X发生的可能性，称为在Y条件下X发生的条件概率，用~P(X|Y)表示
先验概率分布：
P ( Y = c k ) ， k = 1 ， 2 ， . . . ， k P(Y=c_{k})，k=1，2，...，k P(Y=ck)，k=1，2，...，k条件概率分布：
P ( X = x ∣ Y = c k ) = P ( X 1 = x 1 , . . . , X n = x n ∣ Y = c k ) , k = 1 , 2 , . . . , k P(X=x|Y=c_{k})=P(X^{1}=x^{1},...,X^{n}=x^{n}|Y=c_{k}),k=1,2,...,k P(X=x∣Y=ck)=P(X1=x1,...,Xn=xn∣Y=ck),k=1,2,...,k
- 全概率公式： P(X) =P(Y1) x P(X | Y1) x P(Y2) x P(X | Y2) x…x P(Yn) x P(X | Yn)
- 贝叶斯定理： p ( Y = c k ∣ X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) ∑ k P ( X = x ∣ Y = c k ) P ( Y = c k ) p(Y=c_{k}|X=x)=\frac{P(X=x|Y=c_{k})P(Y=c_{k})}{\sum_{k}^{}P(X=x|Y=c_{k})P(Y=c_{k})} p(Y=ck∣X=x)=∑kP(X=x∣Y=ck)P(Y=ck)P(X=x∣Y=ck)P(Y=ck)
区分：
2、朴素贝叶斯理论
- 朴素贝叶斯法通过训练数据集学习联合概率分布P（X，Y），也就是说，通过学习类先验概率分布和类条件概率分布来实现。
- 朴素贝叶斯法对条件概率分布作了条件独立性的假设。其名字来源于贝叶斯定理和一个朴素的假设：所有特征的条件都相互独立于其他给定的响应变量，即特征的条件独立性假设。
条件独立性假设：
P ( X = x ∣ Y = c k ) = ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X=x|Y=c_{k})=\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_{k}) P(X=x∣Y=ck)=∏j=1nP(X(j)=x(j)∣Y=ck)
- 朴素贝叶斯法实际上学习到生成数据的机制，所以属于生成型。条件独立假设等于说明用于分类的特征在类确定的条件下都是条件独立的，该假设使得朴素贝叶斯的学习成为可能。
- 虽然这一假设使得朴素贝叶斯法变得简单，但难免也会牺牲一定的分类准确率。
- 朴素贝叶斯法分类时，对给定的输入x，通过学习到的模型计算后验概率分布 P ( Y = c k ∣ X = x ) P(Y=c_{k}|X=x) P(Y=ck∣X=x)，将后验概率最大的类作为x的类输出。
朴素贝叶斯分类器：
y = f ( x ) = a r g m a x P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) y=f(x)=argmax\frac{P(Y=c_{k})\prod_{j}^{}P(X^{(j)}=x^{(j)}|Y=c_{k})}{\sum_{k}^{}P(Y=c_{k})\prod_{j}^{}P(X^{(j)}=x^{(j)}|Y=c_{k})} y=f(x)=argmax∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck)分母对所有
c k c_{k} ck都相同： y = a r g m a x P ( Y = c k ) ∏ j P ( X j = x j ∣ Y = c k ) y=arg maxP(Y=c_{k})\prod_{j}^{}P(X^{j}=x^{j}|Y=c_{k}) y=argmaxP(Y=ck)∏jP(Xj=xj∣Y=ck)
- 求X用全概率公式，求Y用贝叶斯定理
- 朴素贝叶斯的基本方法：在统计数据的基础上，依据条件概率公式，计算当前特征的样本属于某个分类的概率，选最大的概率分类
- 该模型被称之为朴素是因为它假设对响应变量来说所有的特征都条件独立，但该假设不等同于所有的特征相互独立。
import numpy as np
X = np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
Y = np.array([1,1,1,2,2,2])from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()# 拟合数据
clf.fit(X, Y)print("==[-0.8, -1]预测结果==")print(clf.predict([[-0.8,-1]]))print("==[3,2]预测结果==")print(clf.predict([[3,2]]))
3、贝叶斯决策理论方法
- 在分类问题中，我们会将未知标签的数据集特征与我们已知标签的特征进行比较。朴素贝叶斯，就是这样一种比较的方法。
基本思想：
- 1、已知类条件概率密度参数表达式和先验概率
- 2、利用贝叶斯公式转换成后验概率
- 3、根据后验概率大小进行决策分类
4、朴素贝叶斯分类器实战
- 朴素⻉叶斯分类最适合的场景就是文本分类、情感分析和垃圾邮件识别。其中情感分析和垃圾 邮件识别都是通过⽂本来进⾏判断。
- 从这⾥你能看出来，这三个场景本质上都是文本分类，这 也是朴素⻉叶斯最擅⻓的地⽅。所以朴素⻉叶斯也常⽤于⾃然语⾔处理 NLP 的⼯具。
- sklearn 机器学习包 sklearn 的全称叫 Scikit-learn，它给我们提供了 3 个朴素⻉叶斯分类算法，分别是⾼斯朴 素⻉叶斯（GaussianNB）、多项式朴素⻉叶斯（MultinomialNB）和伯努利朴素⻉叶斯 （BernoulliNB），它们的区别在于特征向量x的分布情况。
根据算法的特征类型将其分成两类。
- 连续：这意味着最终的标签为实值（可以存在小数）
- 离散：这以为着最终的结果为分类的类别值（只能为整数）
5、贝叶斯分类算法
- 贝叶斯分类算法是基于贝叶斯定理和特征条件独立假设的分类方法。
这三种算法适合应⽤在不同的场景下，我们应该根据特征变量的不同选择不同的算法：
高斯朴素贝叶斯
- 高斯朴素贝叶斯（连续）：特征变量是连续变量，符合高斯分布 - 比如说⼈的身高，物体的长度。
#导入相应的包import numpy as np
#导入高斯模型from sklearn.naive_bayes import GaussianNB
#样本X包含三个特征，分别是Red的百分比，Green的百分比，Blue的百分比#每个特征的值都是（0,1）之间的小数#首先我们创建一个训练集
X = np.array([[0.5,0,0.5],[1,1,0],[0,0,0]])#给定我们训练集的分类标签
y = np.array(['Purple','Yellow','Black'])#运用高斯模型去训练数据
clf = GaussianNB()#训练数据集
clf.fit(X, y)#下面我们运用我们的模型进行测试#比如我们试一下，red 0.5，green 0.5，blue 0.5print(clf.predict([[0.5,0.5,0.5]]))
多项式朴素贝叶斯
- 多项式朴素贝叶斯（离散）：特征变量是离散变量，符合多项分布，当特征都是分类型特征时，可使用多项式模型。多项分布描述了在样本标签中的概率分布。
- 可用它来计算特征中分类的出现频率。特别的是，当特征只有两种的时候，将会使用多项式模型中的伯努利模型。 - 在文档分类中特征变量体现在 ⼀个单词出现的次数- 或者是单词的 TF-IDF 值等。
#导入相关的包import numpy as np
#导入多项式模型from sklearn.naive_bayes import MultinomialNB
#我们使用文章最开始的水果的数据集作为示例#水果数据集的样本X具有三个特征[Size, Weight, Color]#每个特征共有三种分类#由于python不能直接识别文字#所以将这个三个特征的不同分类重新编码如下# Size: 0 = Small, 1 = Moderate, 2 = Large# Weight: 0 = Light, 1 = Moderate, 2 = Heavy# Color: 0 = Red, 1 = Blue, 2 = Brown#用编码好的数据创建训练集
X = np.array([[1,1,0],[0,0,1],[2,2,2]])#给训练集的数据创建标签
y = np.array(['Apple','Blueberry','Coconut'])#运用多项式模型训练数据
clf = MultinomialNB()#训练水果数据集
clf.fit(X, y)#预测数据集#比如我们试一下 size = 1，weight = 2，color = 0print(clf.predict([[1,2,0]]))
伯努利朴素贝叶斯
- 伯努利朴素贝叶斯（离散）：特征变量是布尔变量，符合 0/1 分布，通常来说就是二分类标签。上文中提到，当特征只有两种的时候，我们可以使用伯努利模型。
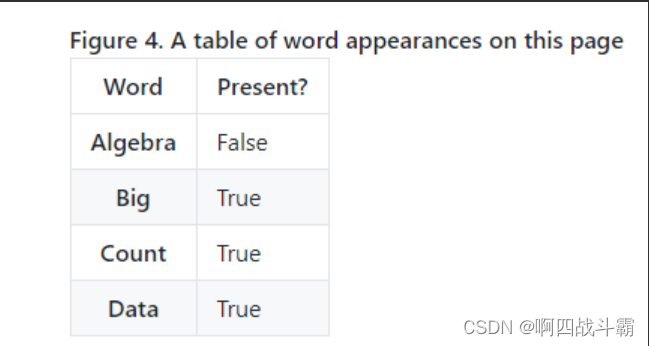
- 与多项式模型不同，在这里只计算一个特征是否发生。 - 比如，本页面是否存在【多项式】这三个字，答案只有两种，存在or不存在。- 伯努利模型的条件概率计算方法与多项式模型一致。 在文档分类中特征是单词是否出现。
#导入包import numpy as np
#导入伯努利模型from sklearn.naive_bayes import BernoulliNB
#数据集X的特征有三个，分别是# Walks like a duck# Talks like a duck# Is small]#这三个特征分别有两种分布，是or否# Walks like a duck: 0 = False, 1 = True# Talks like a duck: 0 = False, 1 = True# Is small: 0 = False, 1 = True#创建训练集
X = np.array([[1,1,0],[0,0,1],[1,0,0]])#给训练集创建标签#是鸭子or不是鸭子
y = np.array(['Duck','Not a Duck','Not a Duck'])#使用伯努利模型训练数据
clf = BernoulliNB()#训练数据集
clf.fit(X, y)#预测数据集#比如我们试一下 三个特征都为true的时候，到底是不是鸭子print( clf.predict([[1,1,1]]))
本文转载自: https://blog.csdn.net/weixin_64215932/article/details/124624363
版权归原作者 七归 所有， 如有侵权，请联系我们删除。
版权归原作者 七归 所有， 如有侵权，请联系我们删除。