目录
1.联合分布函数
定义3 设
(
X
,
Y
)
(X,Y)
(X,Y)为二维随机变量,对任意的
(
x
,
y
)
∈
R
2
(x,y)∈R^2
(x,y)∈R2,称
F
(
x
,
y
)
=
P
(
X
≤
x
,
Y
≤
y
)
F(x,y)=P(X≤x,Y≤y)
F(x,y)=P(X≤x,Y≤y)
为随机变量
(
X
,
Y
)
(X,Y)
(X,Y)的 **(联合)分布函数**.

图3.2 分布函数F(x,y)对应的区域Dxy
F
(
x
,
y
)
F(x,y)
F(x,y)在点
(
x
,
y
)
(x,y)
(x,y)处的函数值,即随机变量
(
X
,
Y
)
(X,Y)
(X,Y)在区域
D
x
y
Dxy
Dxy中取值的概率。
2.实例
实例1
设二维随机变量(X,Y)的联合密度函数为:
f
(
x
,
y
)
=
{
c
y
2
,
0
<
x
<
2
y
,
0
<
y
<
1
0
,
其
它
f(x, y)=\begin{cases} cy^2,\quad 0<x<2y, 0<y<1 \\\\ 0,\quad 其它 \end{cases}
f(x,y)=⎩⎪⎨⎪⎧cy2,0<x<2y,0<y<10,其它
计算:
(1)常数 c c c;
(2)联合分布函数F(x,y);
(3)概率P(|X|≤Y). 解(1)Ω(X,Y)={(x,y):0<x<2y,0<y<1},如图3.9所示.由联合密度函数的规范性得 1 = ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = ∫ 0 1 d y ∫ 0 2 y c y 2 d x = c 2 1=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)dxdy=\int_{0}^{1}dy\int_{0}^{2y}cy^2dx=\frac{c}{2} 1=∫−∞+∞∫−∞+∞f(x,y)dxdy=∫01dy∫02ycy2dx=2c 解得: c = 2 c=2 c=2
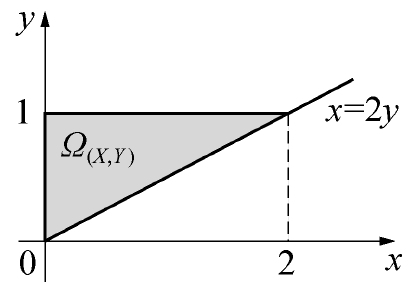
图3.9
(2)由已知得,(看不懂的话,就去看定义7)
当
x
<
0
x<0
x<0 或
y
<
0
y<0
y<0时,
F
(
x
,
y
)
=
0
F(x, y) = 0
F(x,y)=0;
当
0
≤
x
<
2
y
0\leq x<2y
0≤x<2y 且
0
≤
y
<
1
0\leq y<1
0≤y<1 时,
F
(
x
,
y
)
=
∫
0
x
d
u
∫
x
2
y
2
v
2
d
v
=
2
3
x
(
y
3
−
x
3
32
)
F(x, y) = \int_{0}^{x}du\int_{\frac{x}{2}}^{y}2v^2dv=\frac{2}{3}x(y^3-\frac{x^3}{32})
F(x,y)=∫0xdu∫2xy2v2dv=32x(y3−32x3);
当
0
≤
x
<
2
0\leq x<2
0≤x<2 且
y
≥
1
y\geq 1
y≥1 时,
F
(
x
,
y
)
=
∫
0
x
d
u
∫
x
2
1
2
v
2
d
v
=
2
3
x
(
1
−
x
3
32
)
F(x, y) = \int_{0}^{x}du\int_{\frac{x}{2}}^{1}2v^2dv=\frac{2}{3}x(1-\frac{x^3}{32})
F(x,y)=∫0xdu∫2x12v2dv=32x(1−32x3);
当
x
≥
2
y
x\geq 2y
x≥2y 或
0
≤
y
<
1
0\leq y<1
0≤y<1时,
F
(
x
,
y
)
=
∫
0
y
d
v
∫
0
2
y
2
v
2
d
u
=
y
4
F(x, y) = \int_{0}^{y}dv\int_{0}^{2y}2v^2du=y^4
F(x,y)=∫0ydv∫02y2v2du=y4;
当
x
≥
2
x\geq 2
x≥2 或
y
≥
1
y\geq 1
y≥1时,
F
(
x
,
y
)
=
1
F(x, y) = 1
F(x,y)=1;
所以,联合分布函数为,
F
(
x
,
y
)
=
{
0
,
x
<
0
或
y
<
0
2
3
x
(
y
3
−
x
3
32
)
,
0
≤
x
<
2
y
,
0
≤
y
<
1
2
3
x
(
1
−
x
3
32
)
,
0
≤
x
<
2
,
y
≥
1
y
4
,
x
≥
2
y
,
0
≤
y
<
1
1
,
x
≥
2
,
y
≥
1
F(x, y) = \begin{cases} 0,\quad x<0 或y<0\\ \frac{2}{3}x(y^3-\frac{x^3}{32}),\quad 0\leq x<2y, 0\leq y<1 \\\\ \frac{2}{3}x(1-\frac{x^3}{32}), 0\leq x<2, y\geq 1\\ y^4, x\geq 2y, 0\leq y<1\\ 1, x\geq 2, y\geq 1 \end{cases}
F(x,y)=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧0,x<0或y<032x(y3−32x3),0≤x<2y,0≤y<132x(1−32x3),0≤x<2,y≥1y4,x≥2y,0≤y<11,x≥2,y≥1
(3)
显然,对二维连续型随机变量使用联合分布函数刻画其统计规律也是比较复杂的,通常我们使用联合密度函数来描述二维连续型随机变量的概率分布.已知二维连续型随机变量的联合密度函数就可以计算任意事件的概率.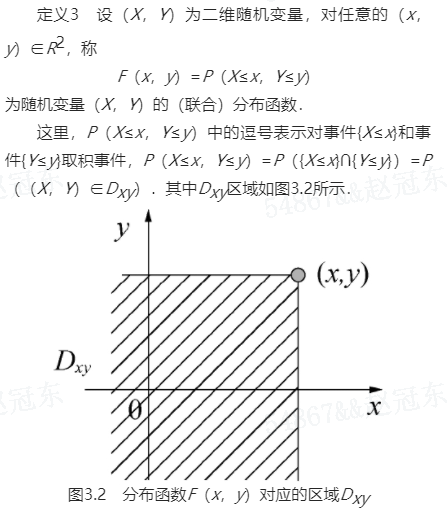
实例2



实例3

定理
定理1 联合分布函数的性质

定义
定义6 二维离散型随机变量


二维离散型随机变量联合分布律的物理解释:考虑
x
o
y
xoy
xoy平面上单位质量的平面薄片,在离散点
(
x
i
,
y
j
)
(x_i,y_j)
(xi,yj)处分布着质点,其质量为
p
i
j
,
i
,
j
=
1
,
2
,
…
.
p_{ij},i,j=1,2,….
pij,i,j=1,2,….这刻画了平面薄片的质量分布情况.
定义7 二维连续型随机变量
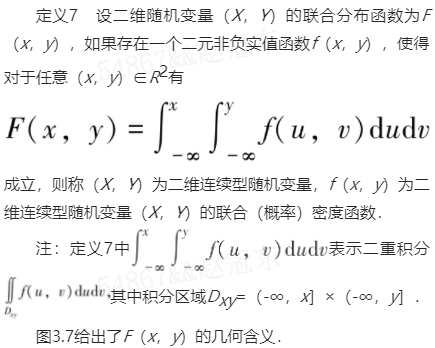
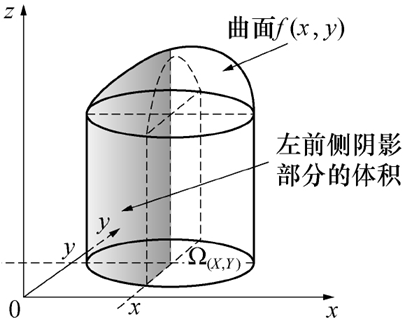
图3.7
二维连续型随机变量联合密度函数的物理解释:考虑xoy平面上单位质量的平面薄片,其在点(x,y)处的面密度为f(x,y),它刻画了平面薄片的质量分布情况.
版权归原作者 赵孝正 所有, 如有侵权,请联系我们删除。