贝叶斯推理三种方法：MCMC 、HMC和SBI

对许多人来说，贝叶斯统计仍然有些陌生。因为贝叶斯统计中会有一些主观的先验，在没有测试数据的支持下了解他的理论还是有一些困难的。本文整理的是作者最近在普林斯顿的一个研讨会上做的演讲幻灯片，这样可以阐明为什么贝叶斯方法不仅在逻辑上是合理的，而且使用起来也很简单。这里将以三种不同的方式实现相同的推理问题。

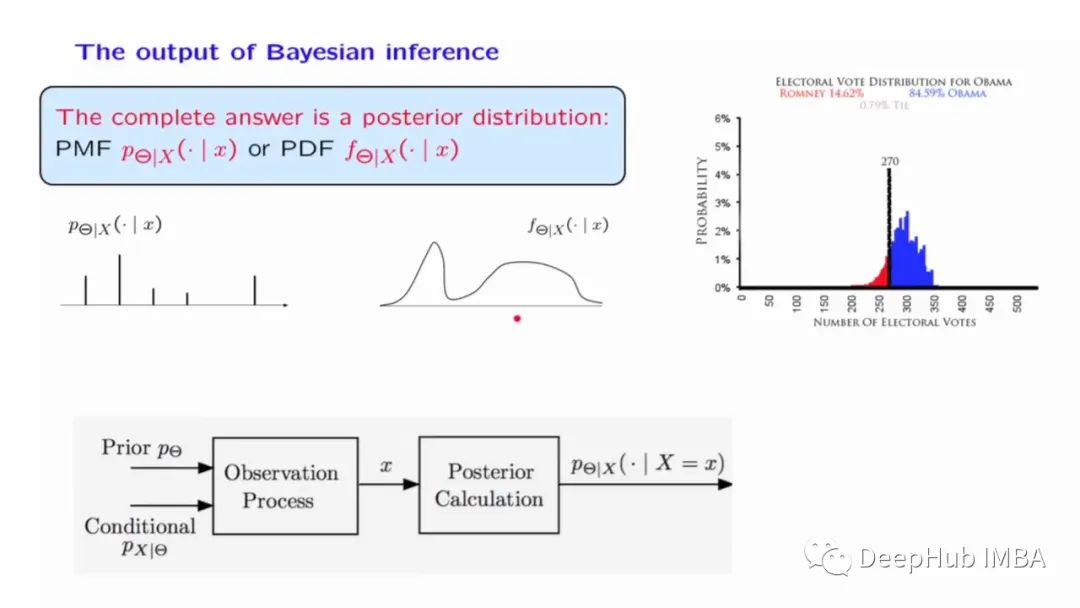
数据

我们的例子是在具有倾斜背景的噪声数据中找到峰值的问题，这可能出现在粒子物理学和其他多分量事件过程中。

首先生成数据：

 %matplotlibinline
 %configInlineBackend.figure_format='svg'
 importmatplotlib.pyplotasplt
 importnumpyasnp
 
 defsignal(theta, x):
     l, m, s, a, b=theta
 
     peak=l*np.exp(-(m-x)**2/ (2*s**2))
     background  =a+b*x
 
     returnpeak+background
 
 defplot_results(x, y, y_err, samples=None, predictions=None):
     fig=plt.figure()
     ax=fig.gca()
     ax.errorbar(x, y, yerr=y_err, fmt=".k", capsize=0, label="Data")
     x0=np.linspace(-0.2, 1.2, 100)
     ax.plot(x0, signal(theta, x0), "r", label="Truth", zorder=0)
 
     ifsamplesisnotNone:
         inds=np.random.randint(len(samples), size=50)
         fori,indinenumerate(inds):
             theta_=samples[ind]
             ifi==0:
                 label='Posterior'
             else:
                 label=None
             ax.plot(x0, signal(theta_, x0), "C0", alpha=0.1, zorder=-1, label=label)
     elifpredictionsisnotNone:
         fori, predinenumerate(predictions):
             ifi==0:
                 label='Posterior'
             else:
                 label=None
             ax.plot(x0, pred, "C0", alpha=0.1, zorder=-1, label=label)
 
     ax.legend(frameon=False)
     ax.set_xlabel("x")
     ax.set_ylabel("y")
     fig.tight_layout()
     plt.close();
     returnfig
 
 # random x locations
 N=40
 np.random.seed(0)
 x=np.random.rand(N)
 
 # evaluate the true model at the given x values
 theta= [1, 0.5, 0.1, -0.1, 0.4]
 y=signal(theta, x)
 
 # add heteroscedastic Gaussian uncertainties only in y direction
 y_err=np.random.uniform(0.05, 0.25, size=N)
 y=y+np.random.normal(0, y_err)
 
 # plot
 plot_results(x, y, y_err)

有了数据我们可以介绍三种方法了

马尔可夫链蒙特卡罗 Markov Chain Monte Carlo

emcee是用纯python实现的，它只需要评估后验的对数作为参数θ的函数。这里使用对数很有用，因为它使指数分布族的分析评估更容易，并且因为它更好地处理通常出现的非常小的数字。

 importemcee
 
 deflog_likelihood(theta, x, y, yerr):
     y_model=signal(theta, x)
     chi2= (y-y_model)**2/ (yerr**2)
     returnnp.sum(-chi2/2)
 
 deflog_prior(theta):
     ifall(theta>-2) and (theta[2] >0) andall(theta<2):
         return0
     return-np.inf
 
 deflog_posterior(theta, x, y, yerr):
     lp=log_prior(theta)
     ifnp.isfinite(lp):
         lp+=log_likelihood(theta, x, y, yerr)
     returnlp
 
 
 # create a small ball around the MLE the initialize each walker
 nwalkers, ndim=30, 5
 theta_guess= [0.5, 0.6, 0.2, -0.2, 0.1]
 pos=theta_guess+1e-4*np.random.randn(nwalkers, ndim)
 
 # run emcee
 sampler=emcee.EnsembleSampler(nwalkers, ndim, log_posterior, args=(x, y, y_err))
 sampler.run_mcmc(pos, 10000, progress=True);

结果如下：

 100%|██████████| 10000/10000 [00:05<00:00, 1856.57it/s]

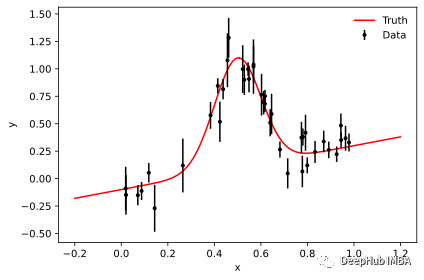
我们应该始终检查生成的链，确定burn-in period，并且需要人肉观察平稳性：

 fig, axes=plt.subplots(ndim, sharex=True)
 mcmc_samples=sampler.get_chain()
 labels= ["l", "m", "s", "a", "b"]
 foriinrange(ndim):
     ax=axes[i]
     ax.plot(mcmc_samples[:, :, i], "k", alpha=0.3, rasterized=True)
     ax.set_xlim(0, 1000)
     ax.set_ylabel(labels[i])
 
 axes[-1].set_xlabel("step number");

现在我们需要细化链因为我们的样本是相关的。这里有一个方法来计算每个参数的自相关，我们可以将所有的样本结合起来:

 tau=sampler.get_autocorr_time()
 print("Autocorrelation time:", tau)
 mcmc_samples=sampler.get_chain(discard=300, thin=np.int32(np.max(tau)/2), flat=True)
 print("Remaining samples:", mcmc_samples.shape)
 
 #结果
 Autocorrelationtime: [122.51626866  75.87228105137.195509    54.63572513  79.0331587 ]
 Remainingsamples: (4260, 5)

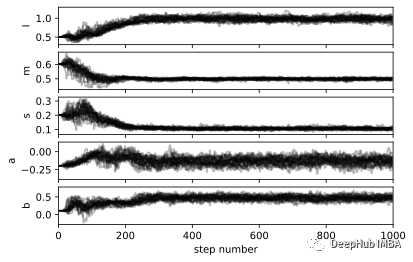
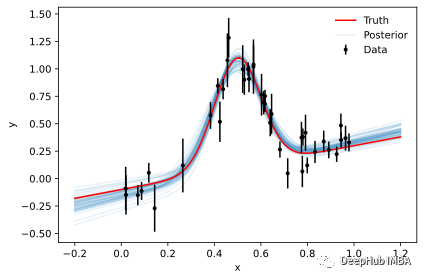
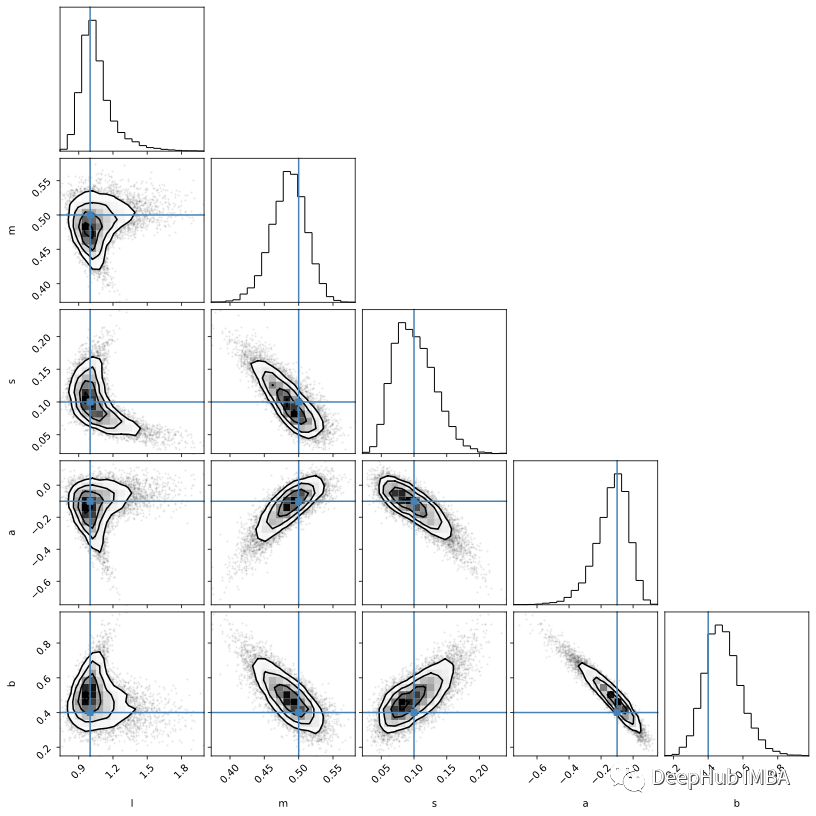
emcee 的创建者 Dan Foreman-Mackey 还提供了这一有用的包corner来可视化样本：

 importcorner
 
 corner.corner(mcmc_samples, labels=labels, truths=theta);

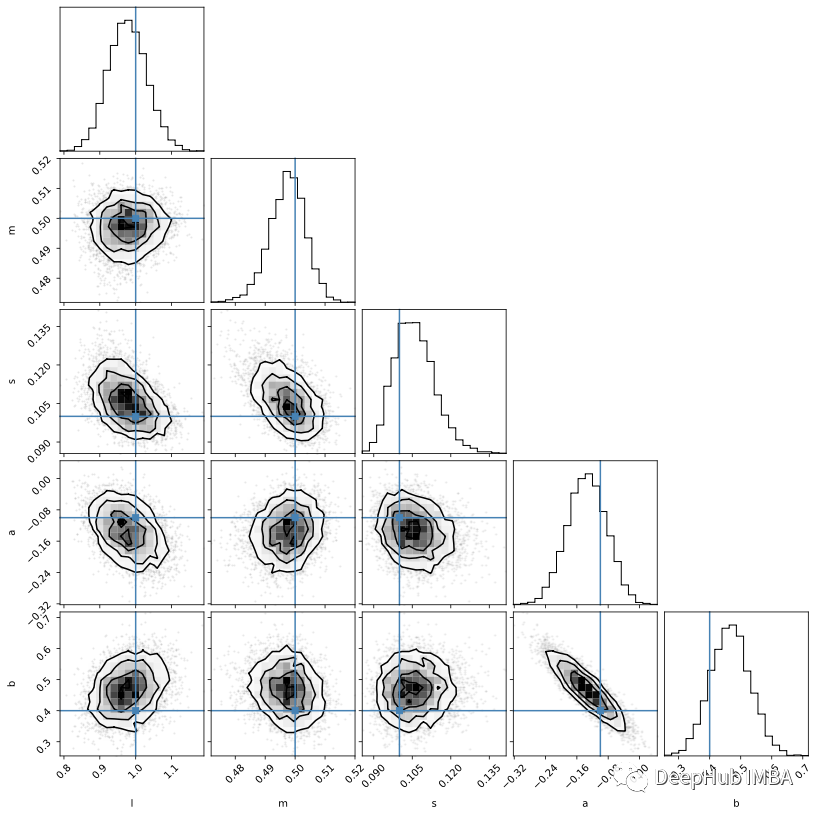
虽然后验样本是推理的主要依据，但参数轮廓本身却很难解释。但是使用样本来生成新数据则要简单得多，因为这个可视化我们对数据空间有更多的理解。以下是来自50个随机样本的模型评估:

 plot_results(x, y, y_err, samples=mcmc_samples)

哈密尔顿蒙特卡洛 Hamiltonian Monte Carlo

梯度在高维设置中提供了更多指导。 为了实现一般推理，我们需要一个框架来计算任意概率模型的梯度。 这里关键的本部分是自动微分，我们需要的是可以跟踪参数的各种操作路径的计算框架。 为了简单起见，我们使用的框架是 jax。因为一般情况下在 numpy 中实现的函数都可以在 jax 中的进行类比的替换，而jax可以自动计算函数的梯度。

另外还需要计算概率分布梯度的能力。有几种概率编程语言中可以实现，这里我们选择了 NumPyro。 让我们看看如何进行自动推理：

 importjax.numpyasjnp
 importjax.randomasrandom
 importnumpyro
 importnumpyro.distributionsasdist
 fromnumpyro.inferimportMCMC, NUTS
 
 defmodel(x, y=None, y_err=0.1):
 
     # define parameters (incl. prior ranges)
     l=numpyro.sample('l', dist.Uniform(-2, 2))
     m=numpyro.sample('m', dist.Uniform(-2, 2))
     s=numpyro.sample('s', dist.Uniform(0, 2))
     a=numpyro.sample('a', dist.Uniform(-2, 2))
     b=numpyro.sample('b', dist.Uniform(-2, 2))
 
     # implement the model
     # needs jax numpy for differentiability here
     peak=l*jnp.exp(-(m-x)**2/ (2*s**2))
     background  =a+b*x
     y_model=peak+background
 
     # notice that we clamp the outcome of this sampling to the observation y
     numpyro.sample('obs', dist.Normal(y_model, y_err), obs=y)
 
 # need to split the key for jax's random implementation
 rng_key=random.PRNGKey(0)
 rng_key, rng_key_=random.split(rng_key)
 
 # run HMC with NUTS
 kernel=NUTS(model, target_accept_prob=0.9)
 mcmc=MCMC(kernel, num_warmup=1000, num_samples=3000)
 mcmc.run(rng_key_, x=x, y=y, y_err=y_err)
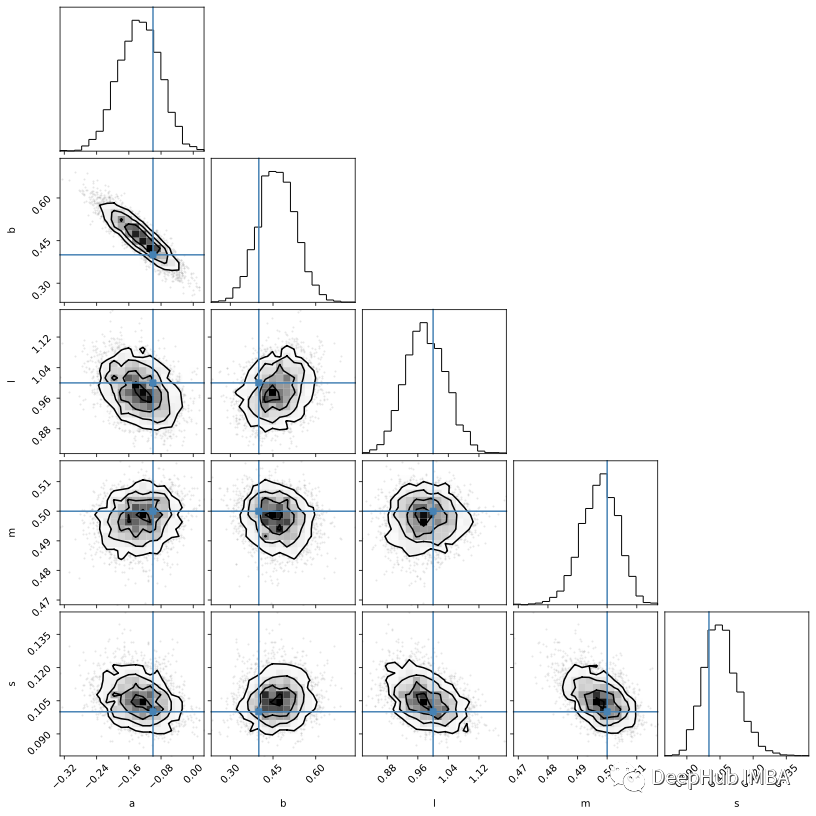
 mcmc.print_summary()
 
 #结果如下：
 sample: 100%|██████████|4000/4000 [00:03<00:00, 1022.99it/s, 17stepsofsize2.08e-01. acc. prob=0.94]
 
 
 
                 mean       std    median      5.0%     95.0%     n_eff     r_hat
          a     -0.13      0.05     -0.13     -0.22     -0.05   1151.15      1.00
          b      0.46      0.07      0.46      0.36      0.57   1237.44      1.00
          l      0.98      0.05      0.98      0.89      1.06   1874.34      1.00
          m      0.50      0.01      0.50      0.49      0.51   1546.56      1.01
          s      0.11      0.01      0.11      0.09      0.12   1446.08      1.00
 
 Numberofdivergences: 0

还是使用corner可视化Numpyro的mcmc结构:

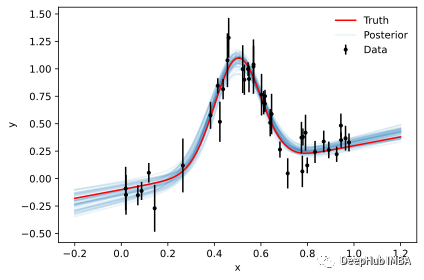
因为我们已经实现了整个概率模型(与emcee相反，我们只实现后验)，所以可以直接从样本中创建后验预测。下面，我们将噪声设置为零，以得到纯模型的无噪声表示:

 fromnumpyro.inferimportPredictive
 
 # make predictions from posterior
 hmc_samples=mcmc.get_samples()
 predictive=Predictive(model, hmc_samples)
 # need to set noise to zero
 # since the full model contains noise contribution
 predictions=predictive(rng_key_, x=x0, y_err=0)['obs']
 
 # select 50 predictions to show
 inds=random.randint(rng_key_, (50,) , 0, mcmc.num_samples)
 predictions=predictions[inds]
 
 plot_results(x, y, y_err, predictions=predictions)

基于仿真的推理 Simulation-based Inference

在某些情况下，我们不能或不想计算可能性。 所以我们只能一个得到一个仿真器（即学习输入之间的映射 θ 和仿真器的输出 D），这个仿真器可以形成似然或后验的近似替代。 与产生无噪声模型的传统模拟案例的一个重要区别是，需要在模拟中添加噪声并且噪声模型应尽可能与观测噪声匹配。 否则我们无法区分由于噪声引起的数据变化和参数变化引起的数据变化。

 importtorch
 fromsbiimportutilsasutils
 
 low=torch.zeros(ndim)
 low[3] =-1
 high=1*torch.ones(ndim)
 high[0] =2
 prior=utils.BoxUniform(low=low, high=high)
 
 defsimulator(theta, x, y_err):
 
     # signal model
     l, m, s, a, b=theta
     peak=l*torch.exp(-(m-x)**2/ (2*s**2))
     background  =a+b*x
     y_model=peak+background
 
     # add noise consistent with observations
     y=y_model+y_err*torch.randn(len(x))
 
     returny

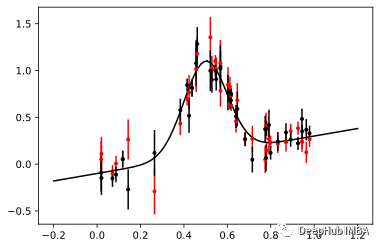
让我们来看看噪声仿真器的输出:

 plt.errorbar(x, this_simulator(torch.tensor(theta)), yerr=y_err, fmt=".r", capsize=0)
 plt.errorbar(x, y, yerr=y_err, fmt=".k", capsize=0)
 plt.plot(x0, signal(theta, x0), "k", label="truth")

现在，我们使用 sbi 从这些模拟仿真中训练神经后验估计 (NPE)。

 fromsbi.inference.baseimportinfer
 
 this_simulator=lambdatheta: simulator(theta, torch.tensor(x), torch.tensor(y_err))
 
 posterior=infer(this_simulator, prior, method='SNPE', num_simulations=10000)

NPE使用条件归一化流来学习如何在给定一些数据的情况下生成后验分布：

 Running 10000 simulations.:   0%|          | 0/10000 [00:00<?, ?it/s]
 Neural network successfully converged after 172 epochs.

在推理时，以实际数据 y 为条件简单地评估这个神经后验：

 sbi_samples=posterior.sample((10000,), x=torch.tensor(y))
 sbi_samples=sbi_samples.detach().numpy()

可以看到速度非常快几乎不需要什么时间。

 Drawing 10000 posterior samples:   0%|          | 0/10000 [00:00<?, ?it/s]

然后我们再次可视化后验样本：

 corner.corner(sbi_samples, labels=labels, truths=theta);

 plot_results(x, y, y_err, samples=sbi_samples)

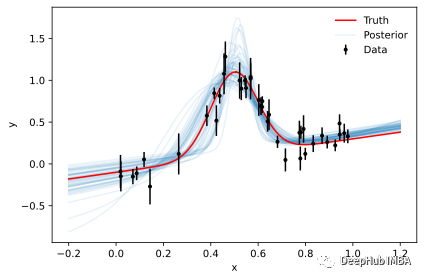
可以看到仿真SBI的的结果不如 MCMC 和 HMC 的结果。 但是它们可以通过对更多模拟进行训练以及通过调整网络的架构来改进（虽然并不确定改完后就会有提高）。

但是我们可以看到即使在没有拟然性的情况下，SBI 也可以进行近似贝叶斯推理。

作者：Peter Melchior