SPSS学习相关性分析

进行相关分析

双变量相关计算变量之间

皮尔逊相关系数(直接解读) 
肯德尔(需要计算偏相关性)
斯皮尔曼(需要通过`*`与`**`的大小进行判断)

一. 分析花瓣长、花枝长与花萼长两两相关性关系

采用皮尔逊双尾检验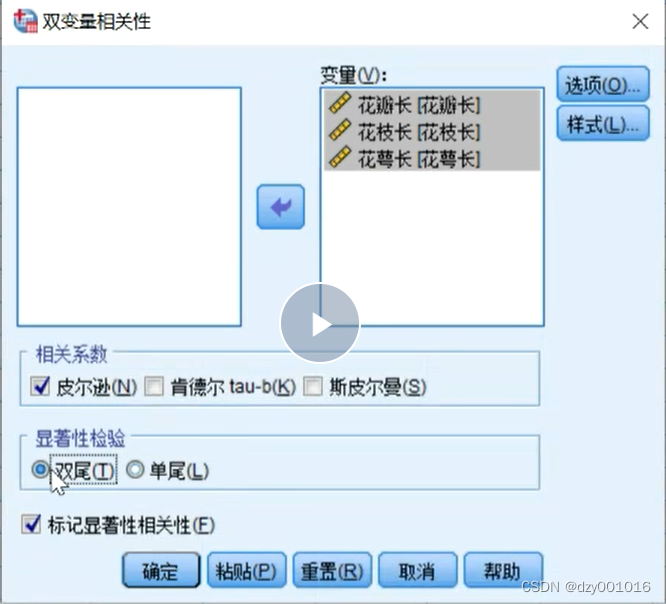
在这里插入图片描述

显著性检验
 双尾(双侧检验) 以0.01为检验标准
 单尾(单侧检验) 以0.05为检验标准

数据为对称矩阵(对角线为1)

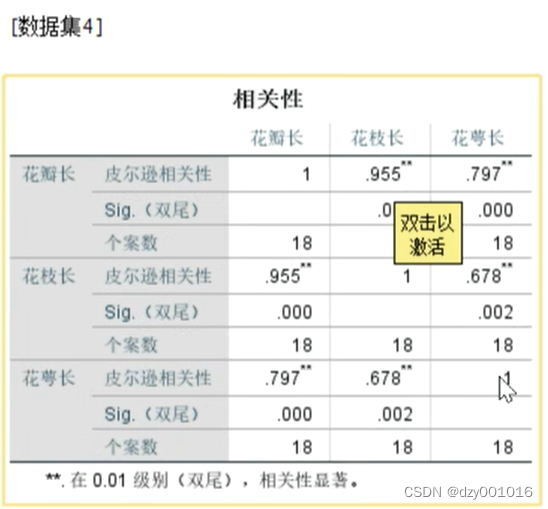
在这里插入图片描述

上图的Sig.(双尾) 与花枝长的系数为0.00 < 0.01 => 有相关性系数有效

二. 分析地位域、权威主义与顺从性两两相关性关系

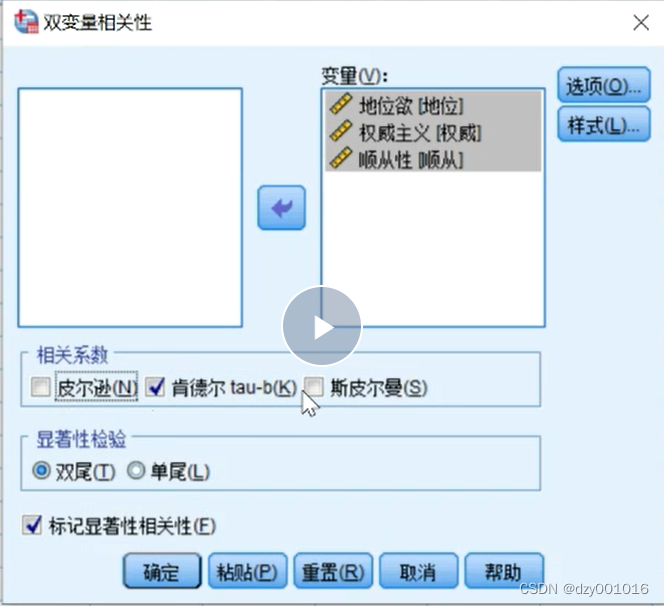
在这里插入图片描述

数据分析

采用肯德尔斯皮尔曼双尾检验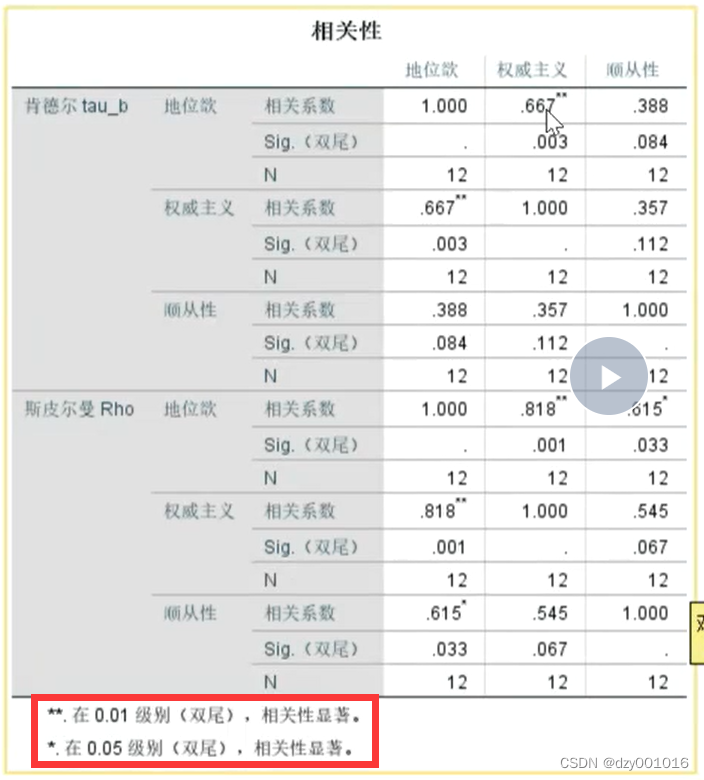
在这里插入图片描述

肯德尔计算三个数之间哪两个相关性更大可以使用偏相关系数

在这里插入图片描述

代入计算得 R

     x 
    
   
     y 
    
   
     z 
    
   
  
    xyz 
   
  
xyz=0.62 => 即偏相关系数更接近与Y =>  
 
  
   
   
     X 
    
   
  
    X 
   
  
X与 
 
  
   
   
     Y 
    
   
  
    Y 
   
  
Y的相关性与 
 
  
   
   
     Z 
    
   
  
    Z 
   
  
Z无关

斯皮尔曼的相关系数一行可以看出在那一级别(双尾)下相关性更强

0.818 > 0.615 => 地位欲在0.01级别时相关性更为显著

观察数值处于正负1附近时数值相关性更大

距离相关计算记录(样本)之间

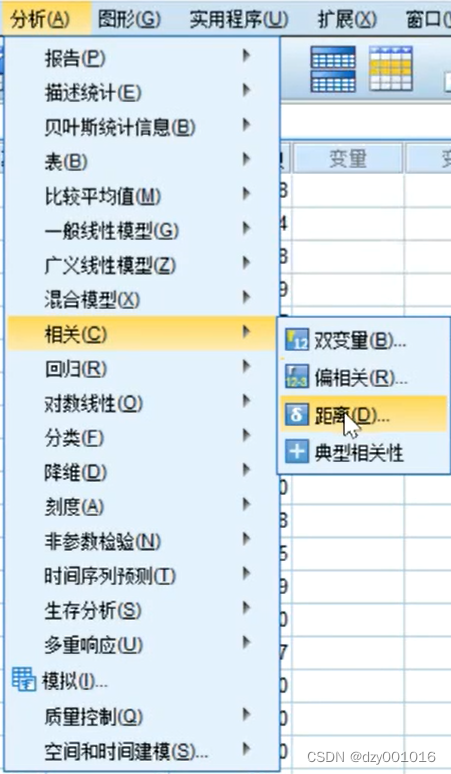
在这里插入图片描述

三.分析国家之间在森林面积、森林覆盖率、林木蓄积量与草原面积之间的相关性

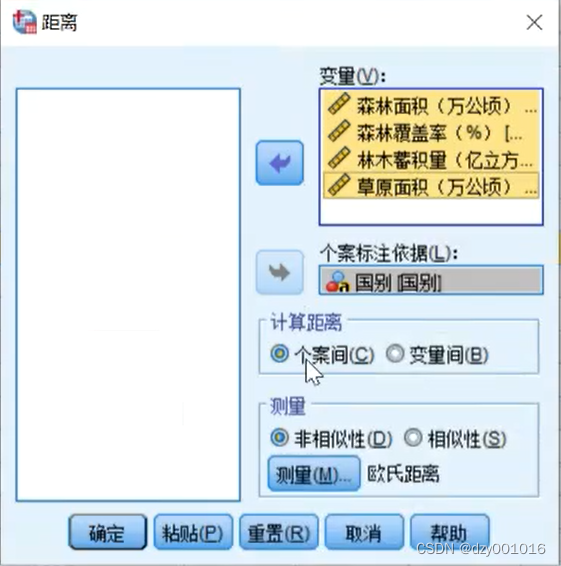
在这里插入图片描述

分析数据进行聚类分析

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eUeuh1Wl-1653913332030)(file:///C:/Users/丁子川/AppData/Roaming/marktext/images/2022-05-29-11-07-17-image.png)]

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NbC1KieE-1653913332031)(file://C:\Users\丁子川\AppData\Roaming\marktext\images\2022-05-29-11-07-34-image.png)]$

系统聚类

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qm7XNrjJ-1653913332032)(file:///C:/Users/丁子川/AppData/Roaming/marktext/images/2022-05-29-11-14-51-image.png)]

通过系统聚类将上述国家进行动态聚类

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C5jF0Ut7-1653913332032)(file:///C:/Users/丁子川/AppData/Roaming/marktext/images/2022-05-29-11-17-03-image.png)]

可以看出使用平方欧式距离来进行聚类将7与15记录聚在一起

下一阶段是阶段6 再将记录4聚在一起

垂直冰柱图(直观动态归类过程)

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Sx5CVi8C-1653913332033)(file://C:\Users\丁子川\AppData\Roaming\marktext\images\2022-05-29-11-24-50-image.png)]$

可以看到垂直冰柱图的最低是 7与15 之间的柱子再是 11与16 之间的柱子再是 4与14 之间的柱子再是 14与12 之间(即4与14与12 归为一类) 以此类推

可以自定义聚类统计等

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9SA1Ee4E-1653913332034)(file:///C:/Users/丁子川/AppData/Roaming/marktext/images/2022-05-29-11-32-34-image.png)]

可以看到分类变为自定义的个数

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-v7tpLmOv-1653913332035)(file:///C:/Users/丁子川/AppData/Roaming/marktext/images/2022-05-29-11-35-57-image.png)]

也可以在生成结果中添加图

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pOX36pda-1653913332036)(file:///C:/Users/丁子川/AppData/Roaming/marktext/images/2022-05-29-11-37-08-image.png)]

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vtgGxVFT-1653913332037)(file://C:\Users\丁子川\AppData\Roaming\marktext\images\2022-05-29-11-37-43-image.png)]$

数据转置
常用于将以行为数据参数的记录转置为列排
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yePEz83C-1653913332038)(file:///C:/Users/丁子川/AppData/Roaming/marktext/images/2022-05-29-11-42-36-image.png)]

K-均值聚类

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6txVHjZl-1653913332039)(file://C:\Users\丁子川\AppData\Roaming\marktext\images\2022-05-29-11-50-25-image.png)]$

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AanQYHRS-1653913332039)(file://C:\Users\丁子川\AppData\Roaming\marktext\images\2022-05-29-11-51-45-image.png)]$

数据分析
在这里插入图片描述

标签：概率论数据分析人工智能

本文转载自: https://blog.csdn.net/dzy001016/article/details/125053278
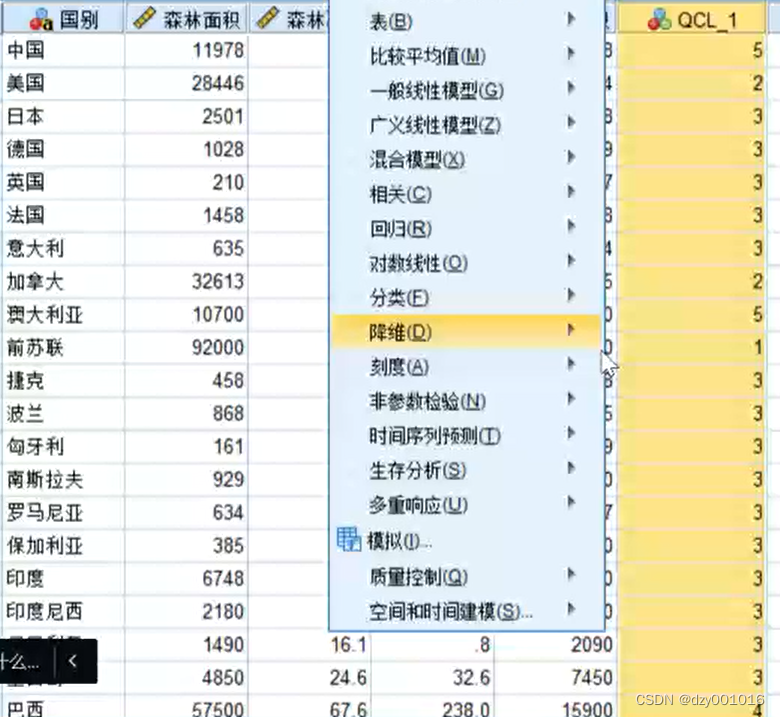
版权归原作者 dzy001016 所有，如有侵权，请联系我们删除。

SPSS学习相关性分析

进行相关分析

一. 分析花瓣长、花枝长与花萼长两两相关性关系

二. 分析地位域、权威主义与顺从性两两相关性关系

三.分析国家之间在森林面积、森林覆盖率、林木蓄积量与草原面积之间的相关性

系统聚类

K-均值聚类

发表评论