假设我们从未知分布 q 中观察到 N 个独立且同分布的 (iid) 样本 X = (x1, ... , xN)。统计学中的一个典型问题是“样本集 X 能告诉我们关于分布 q 的什么信息?”。
参数统计方法假设 q 属于一个参数分布族,并且存在一个参数 θ,其中 q(x) 等于所有 x 的参数分布 p(x|θ);例如,p(.|θ) 可以是具有单位方差的正态分布,其中 θ 表示平均值。在这种情况下,问题是“X 告诉我们关于 q 的什么?”或者说“如果我们有 q = p(.|θ) 的参数 θ,X 告诉我们什么呢?”。
回答这个问题的贝叶斯方法是使用概率论规则并假设 θ 本身是具有先验分布 p(θ) 的随机变量。先验分布 p(θ) 是我们在观察任何样本之前对 θ 的假设和猜测的形式化。在这种前提下,我们可以将参数和数据的联合概率分布写在一起:
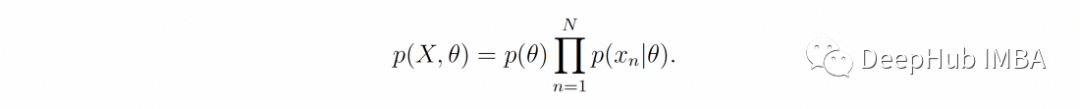
利用这个公式,X捕捉到的关于θ的所有信息都可以总结为后验分布
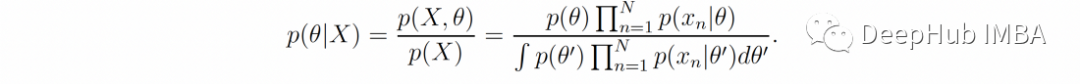
贝叶斯统计是自洽且优雅的:一切都可以使用概率论的规则自然推导出来的,而且假设总是明确且清晰的。但是它通常看起来很神秘和令人费解:(i)我们能从后验分布 p(θ|X) 中真正学到什么关于底层分布 q 的信息?还有(ii)如果我们的假设不成立,例如,如果 q 不属于我们考虑的参数族,该信息的可靠性如何?
在这篇文章中,我们将对这两个问题进行解释。分析样本数量 N 很大时后验分布的渐近形式——这是研究贝叶斯推理的常用方法。然后,我展示了一般理论如何适用于高斯族的简单情况。最后,在三个案例研究中,我使用模拟和分析,后验分布如何与数据的底层分布相关,以及随着N的增加,这个链接如何变化。¹。
理论:大 N 的渐近情况
等式 1 中后验分布的对数可以重新表述为
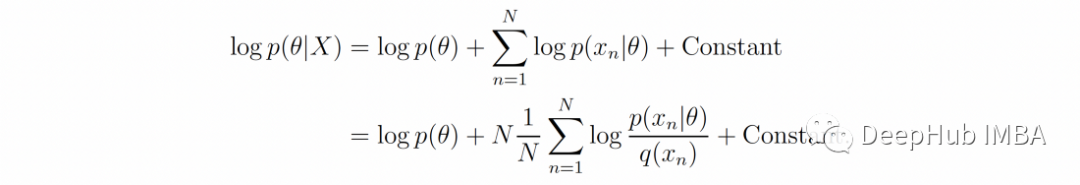
等式 2 中的常数(相对于 θ)仅对后验概率分布的归一化很重要,并不影响它作为 θ 的函数变化。所以对于大 N,我们可以使用大数定律,并通过以下方式近似等式 2 中的第二项(对数似然之和)
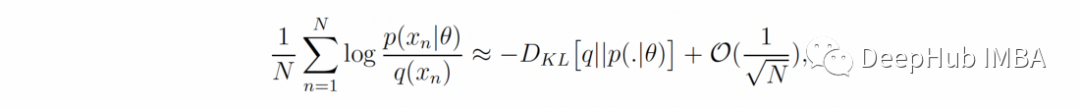
其中 D-KL 是 Kullback-Leibler 散度,是测量真实分布 q 和参数分布 p(.|θ) 之间的伪距离。要注意的重要的一点是,仅当 log p(x|θ) 的均值和方差(相对于 q)对于某些参数 θ 是有限的时,近似才有效。我们将在下一节进一步讨论这种情况的重要性。
如果 p(θ) 完全支持参数空间(即始终为非零),则 log p(θ) 始终是有限的,并且等式 2 中对于大 N的的主要项是 D-KL [q | | p(.|θ)] 乘以 N。这意味着增加样本数 N 会使后验分布 p(θ|X) 越来越接近分布
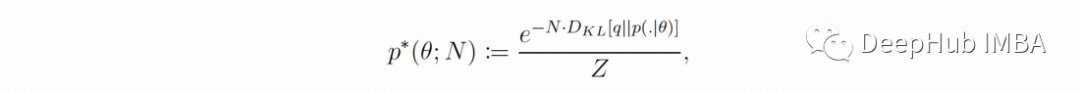
这是公式3,其中 Z 是归一化常数。p*(θ; N) 是一个有趣的分布:它的最大值是散度 D-KL [q || p(.|θ)] 最小值(即当 p(.|θ) 尽可能接近 q)² 时,它对 D-KL [q || p(.|θ)] 随着样本数量 N 的增加而增加(即,随着 N 的增加,它在其最大值附近变得更加“窄”)。
当假设正确时
当假设是正确的并且存在q = p(.|θ*)的 θ*时,
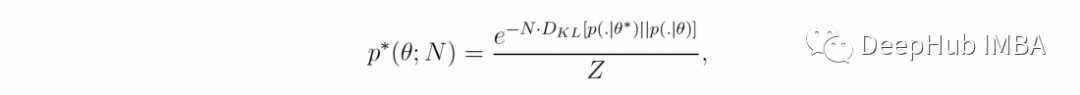
其中 D-KL [p(.|θ*) || p(.|θ)] 是 θ 和 θ* 之间的伪距离。因此随着 N 的增加,后验分布集中在真实参数 θ* 周围,这可以为我们提供了完全识别 q 所需的所有信息³。
当假设错误时
当没有 q = p(.|θ) 的 θ 时,我们永远无法识别真正的潜在分布 q — 因为我们没有在正确的位置搜索!强调这个问题是因为这种情况不仅限于贝叶斯统计,还扩展到任何参数统计方法。
尽管在这种情况下我们永远无法完全识别 q,但后验分布仍然可以提供有关 q 的信息:如果我们将 θ* 定义为 q 在参数族空间上的伪投影的参数:
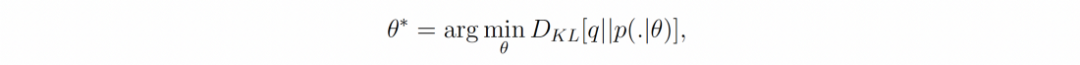
那么随着 N 的增加,后验分布集中在 θ* 周围,为我们提供了足够的信息来确定 q 的参数族中的最佳候选者⁴。
理论的总结
随着N的增加,后验分布集中在参数θ*周围,该参数描述了参数族中最接近实际分布q的分布。如果q属于参数族,那么最接近q的分布就是q本身。下面我们看三个例子:
高斯分布
上面我们研究了大量样本的后验分布的一般形式。我们首先研究一个简单的例子,看看一般理论如何适用于具体案例。
这里是一个简单的例子,我们的参数分布是具有单位方差和均值等于 θ 的高斯分布:
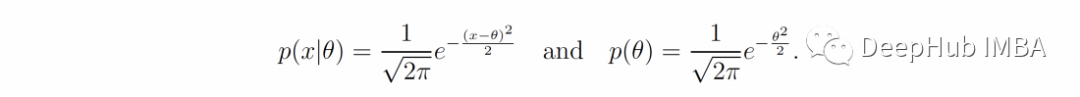
为了简单起见,我们只考虑一个标准正态分布作为先验p(θ)。利用公式1可以很容易得到后验分布为
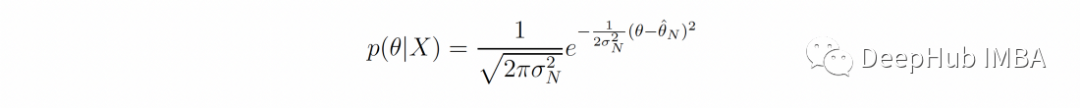
这里的
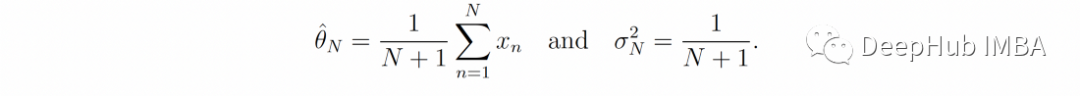
现在,还可以得到 p*(θ; N)(公式 3)并将其与后验分布进行比较:只要真实分布 q 的均值和方差是有限的,我们就有
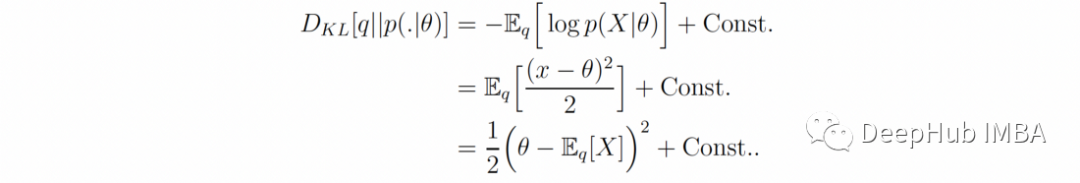
还是根据公式3,可以得到
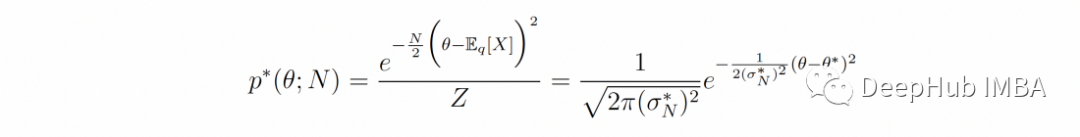
这里的
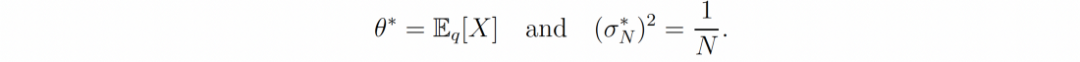
我们把它称作公式4 ,根据一般理论,可以用p*(θ;N)表示大N,因为
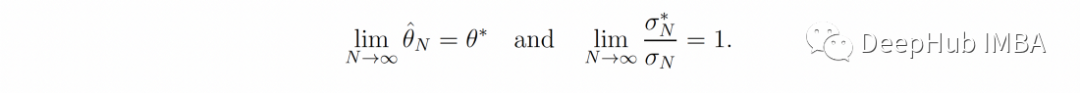
这样可以看到,p(θ|X) 集中在潜在分布 q 的真实均值附近——如果它存在的话。
模拟研究
上面的理论分析有两个关键假设:(i) N 很大,(ii) log p(x|θ) 的均值和方差(相对于 q)对于某些 θ 是有限的。所以 在本节中,我们使用模拟并研究如果这些假设不成立,我们的发现也是非常稳健的。
还是使用上一节中示例,即具有单位方差的高斯分布族。然后考虑 q 的三种不同选择,并分析后验 p(θ|X) 随着 N 增加的变化。
我们还要研究 q 的最大后验 (MAP) 估计 q-MAP-N = p(.|θ-hat-N) 如何随着 N 的增加而变化,其中 θ-hat-N 是 p( θ|X)。,因为这有助于我们了解通过查看后验分布的最大值⁵ 来识别真实分布 q 的精确度。
高斯分布
第一种情况,q 属于参数族并且满足所有假设,这是我们希望的最佳情况:
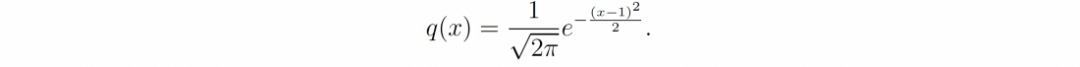
从q中抽取了10000个样本,发现后验分布p(θ|X=(x1,…,xN))和MAP估计q-MAP-N -,通过在N = 1到10000之间逐一添加样本(下图1)。可以看到随着N的增加,p(θ|X)集中在真参数周围(图1,左),MAP估计收敛于真分布q(图1,右)。
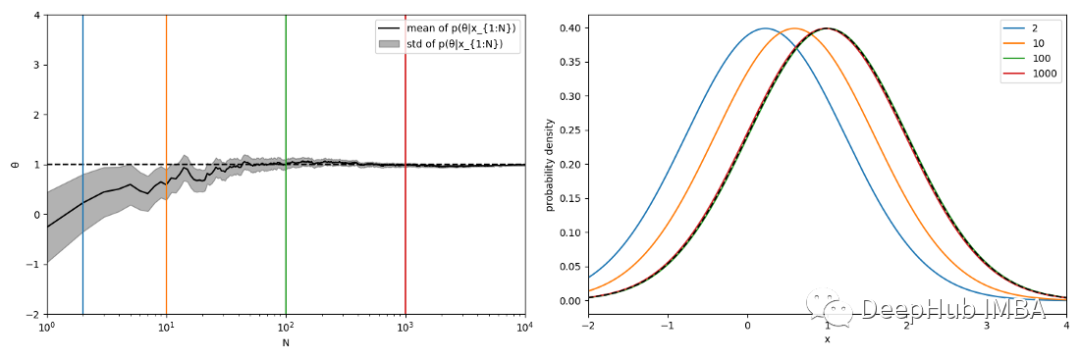
左:后验分布的均值(实黑色曲线)和标准差(灰色阴影区域)作为n的函数。虚线的黑线表示q=p(.|θ=1)的真参数。后验分布收敛于真参数。垂直的彩色线分别表示N=2、10、100和1000。右:当N=2、10、100和1000(彩色曲线)时q的MAP估计值。黑色虚线曲线表示真实分布q。
拉普拉斯分布
这是第二种情况,一个具有单位均值的拉普拉斯分布作为真实分布:
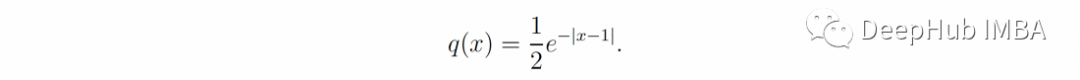
在这种情况下,q不属于参数族,但它仍然有一个有限的均值和方差。根据理论后验分布应该集中在参数族上q伪投影的参数θ附近。对于高斯族的例子,θ总是底层分布的平均值,即θ* = 1(公式4)。
模拟表明随着N的增加,p(θ|X)确实集中在θ* = 1附近(图2,左)。MAP估计收敛于一个系统上不同于真实分布q的分布(图2,右),这是因为我们在高斯分布中搜索拉普拉斯分布!这本质上是任何参数统计方法的一个问题:如果你在错误的地方搜索,你就找不到正确的分布!
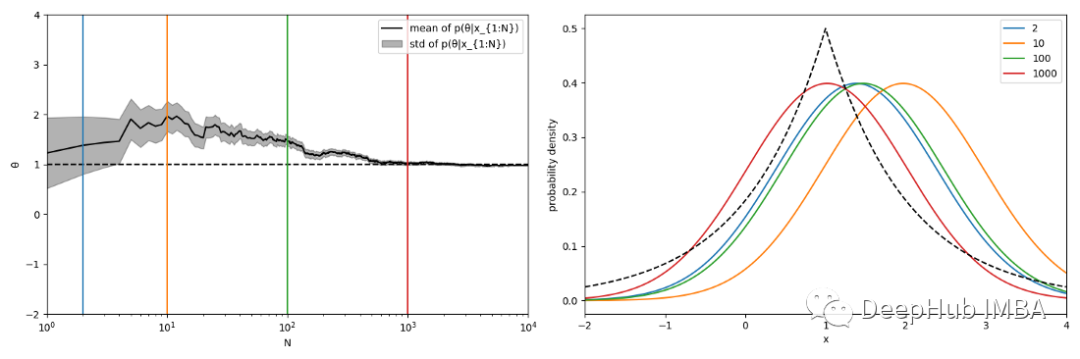
左:后验分布作为n的函数的均值(实黑色曲线)和标准差(灰色阴影区域)。虚线的黑线表示的是q在参数族上的伪投影对应的参数,即θ*=1(公式4)。后验分布收敛于θ*。垂直的彩色线表示N=2、10、100和1000。右:当N=2、10、100和1000(彩色曲线)时q的MAP估计值。黑色虚线曲线表示真实分布q。
柯西分布
第三种也是最后一种情况,我们选择最坏的情况并考虑柯西分布(著名的重尾分布)作为真实分布:
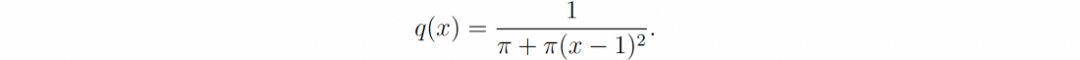
在这种情况下,q 不属于参数族,但更关键的问题是柯西分布没有明确定义的均值或有限方差:这违反了所有理论的假设!
看看我们模拟的情况,模拟表明 p(θ|X) 不会收敛到任何分布(图 3,左):p(θ|X) 的标准差变为零并且集中在其均值附近,但均值本身并不收敛并且会从一个值跳转到另一个值。这个问题的解释很简单:柯西分布和高斯分布之间的 KL 散度是无限的,并且与它们的参数无关!也就是根据 KL 散度,所有高斯分布均等地(并且无限地)远离 q,因此没有偏好选择哪一个作为其估计!
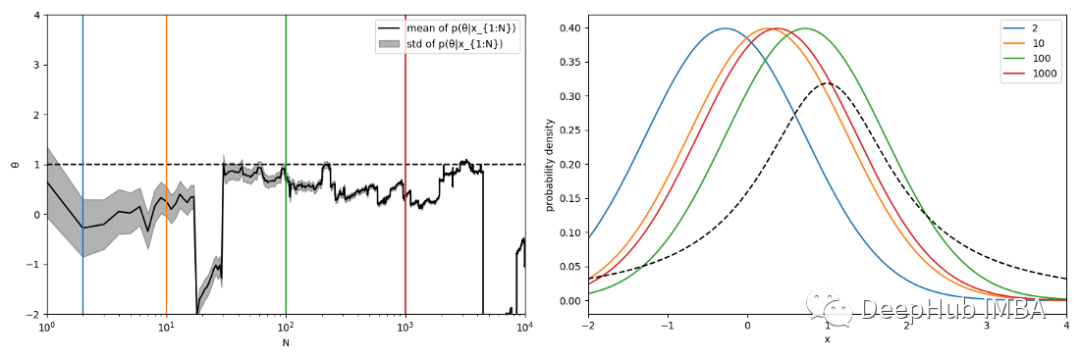
图 3. q 的柯西分布。左:作为 N 函数的后验分布的均值(实线黑色曲线)和标准偏差(阴影灰色区域)。黑色虚线显示 q 的中值:如果 q 有均值,则因为对称该均值肯定等于 1 。后验分布不会收敛到任何分布,其均值会从一个值跳到另一个值。垂直彩色线显示 N=2、10、100 和 1000。右图:对 N=2、10、100 和 1000 的 q 的 MAP 估计(彩色曲线)。黑色虚线曲线显示真实分布 q。
总结
如果我们假设的分布的参数族与真实分布q相差不大,那么后验分布总是集中在一个参数周围,该参数在某种程度上提供了关于q的信息。
如果q不属于参数族,那么这些信息可能只是边缘的,并不是真正有用的。最坏的情况是当q与参数族中的任何分布相差太大时:在这种情况下,后验分布是无法提供任何信息的。
作者:Alireza Modirshanechi