贝叶斯分类器
贝叶斯分类器是一种概率框架下的统计学习分类器,对于分类任务而言,假设在相关概率都已经知道的情况下,贝叶斯分类器考虑如何基于这些概率为样本判定最优的类标,在开始介绍贝叶斯决策论之前,我们首先回顾下概率论委员会常委——贝叶斯公式:
定理:假设实验
E
E
E的样本空间
S
S
S,A为E的事件,
B
1
,
B
2
,
.
.
.
,
B
n
B_1,B_2,...,B_n
B1,B2,...,Bn为
S
S
S的一个划分,且
P
(
A
)
>
0
,
P
(
B
i
)
>
0
/
/
P(A)>0,P(B_i)>0//
P(A)>0,P(Bi)>0//(i = 1,2,3,…,n),则:
P
(
B
i
∣
A
)
=
P
(
A
∣
B
i
)
P
(
B
i
)
∑
j
=
1
n
P
(
A
∣
B
j
)
P
(
B
j
)
P(B_i|A) = \frac{P(A|B_i)P(B_i)}{\sum_{j= 1}^nP(A|B_j)P(B_j)}
P(Bi∣A)=∑j=1nP(A∣Bj)P(Bj)P(A∣Bi)P(Bi)
称为贝叶斯公式:
若将上述定义中的样本空间划分
B
i
B_i
Bi看作类标,A看作一个新的样本,则很容易将条件概率理解为样本
A
A
A是类别
B
B
B的概率,在机器学习训练模型的过程中,往往我们都试图去优化一个风险函数,因此,在概率框架下,我们都可以为**贝叶斯定义为条件概率**:(conditional risk)
R
(
C
i
∣
x
)
=
∑
j
=
1
N
λ
i
j
P
(
C
j
∣
x
)
R(C_i|x) = \sum_{j = 1}^N\lambda_{ij}P(C_j|x)
R(Ci∣x)=j=1∑NλijP(Cj∣x)
我们的任务就是寻找一个判定准则最小化所有样本的条件风险总和,因此,就有了贝叶斯判定准则,为最小化总体风险,只需在每个样本上选择那个使得条件风险最小的类别:
h
∗
(
x
)
=
a
r
g
m
i
n
c
∈
y
R
(
c
∣
x
)
h^*(x) = argmin_{c\in y}R(c|x)
h∗(x)=argminc∈yR(c∣x)
若损失函数
λ
\lambda
λ取0-1损失,则有:
R
(
C
∣
X
)
=
1
−
P
(
c
∣
x
)
R(C|X) = 1 - P(c|x)
R(C∣X)=1−P(c∣x)
h
∗
(
x
)
=
a
r
g
m
a
x
c
∈
v
P
(
c
∣
x
)
h^*(x) = argmax_{c\in v}P(c|x)
h∗(x)=argmaxc∈vP(c∣x)
即对每个样本
x
x
x,选择后实概率,
p
(
C
∣
X
)
p(C|X)
p(C∣X),一般这里两种策略来对后实概率进行估计。
- 判别式模型,直接对 P ( c ∣ x ) P(c|x) P(c∣x)进行建模求解,;例如,我们前面所介绍的决策树,神经网络、SVM都属于判别式模型。
- 生成式模型,通过先对联合分布 P ( x , c ) P(x,c) P(x,c)建模,从而进一步求解,
P ( c ∣ x ) P(c|x) P(c∣x)- 贝叶斯分类器就属于生成式模型,基于贝叶斯公式对后验概率 P ( c ∣ x ) P(c|x) P(c∣x)进行一项神奇的变换,
P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) P(c|x) = \frac{P(c)P(x|c )}{P(x)} P(c∣x)=P(x)P(c)P(x∣c)
对于给定的样本
x
x
x,
p
(
X
)
p(X)
p(X)与类无关,
P
(
c
)
P(c)
P(c)称为类先验概率,
P
∗
∗
加粗样式
∗
∗
(
x
∣
c
)
P**加粗样式**(x|c)
P∗∗加粗样式∗∗(x∣c)称为类条件概率,这时估计后验概率
P
(
c
∣
x
)
P(c|x)
P(c∣x)就变成**为估计类先验概率和类条件概率的问题**。对于先验概率和后验概率,这里普及以下它们的基本概念:
*先验概率,根据以往的经验和分析得到的概率,
- 后验概率:后验概率是基于新的信息,修正原来的先验概率后所获得的更接近实际情况的概率估计。
实际上先验概率就是在没有任何结果出来的情况下估计的概率,而后验概率则是在有一定依据后的重新估计,直观意义上后验概率就是条件概率。下面直接上Wiki上的一个例子,简单粗暴快速完事…
回归正题,对于类先验概率
P
(
c
)
P(c)
P(c),
p
(
c
)
p(c)
p(c)就是**样本空间中各类样本所占的比例**,根据大数定理(当**样本足够多时,频率趋于稳定等于其概率**),这样当训练样本充足时,p©可以使用各类出现的频率来代替。因此只剩下类条件概率
p
(
x
∣
c
)
p(x | c )
p(x∣c),它表达的意思是在类别
c
c
c中出现
x
x
x的概率,它涉及**到属性的联合概率问题,若只有一个离散属性**还好,当属性**多时采用频率估计起来就十分困难**,因此这里一般采用**极大似然法**进行估计。
极大似然估计
极大似然估计(Maximum Likelihood Estimation,简称MLE),是一种根据数据采样来估计概率分布的经典方法。常用的策略是先假定总体具有某种确定的概率分布,再基于训练样本对概率分布的参数进行估计。运用到类条件概率
p
(
x
∣
c
)
p(x | c )
p(x∣c)中,假设
p
(
x
∣
c
)
p(x | c )
p(x∣c)服从一个**参数为θ的分布**,问题就变为根据已知的训练样本来估计θ。极大似然法的核心思想就是:估计**出的参数使得已知样本出现的概率最大,即使得训练数据的似然最**大。

有时间,将分类器的都好好研究一遍,各种分类器啥都认真研究一遍,全部都将其搞定都行啦的样子。
- 写出似然函数
- 对似然函数取对数,并整理
- 求偏导,令偏导为0,得到似然方程组。
- 解似然方程组,得到所有参数即为所求。
例如:假设样本的属性都为连续值,
P
(
x
∣
c
)
P(x|c)
P(x∣c)是一个多维高斯分布,则通过MLE计算出参数刚好分别为“:
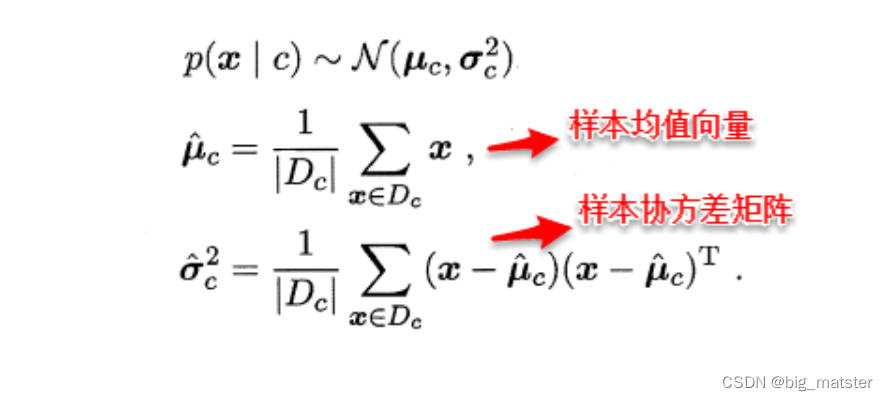
上述看起来十分呵护逻辑,但是采用最大似然估计参数的效果很大程度上依赖于做出假设是否合理,是否符合潜在的真实数据分布,这就需要大量的经验知识,
朴素贝叶斯分类器
不难看出,原始的贝叶斯分类器的最大问题在于联合概率密度函数的估计,首先需要根据经验来假设联合概率分布,其次当属性很多时,训练样本往往覆盖不够,参数的估计会出现很大的偏差。为了避免这个问题,朴素贝叶斯分类器采用了属性条件独立性假设,即样本数据所有属性之间相互独立,这样类条件概率
p
(
x
∣
c
)
p(x|c)
p(x∣c)可以改写为:
P
(
x
∣
c
)
=
∏
i
=
1
d
p
(
x
i
∣
c
)
P(x|c) = \prod_{i = 1}^dp(x_i|c)
P(x∣c)=i=1∏dp(xi∣c)
这样为每个样本估计类条件概率变成为每个样本的每个属性估计类条件概率。
相比较原始的贝叶斯分类器,朴素贝叶斯分类器基于单个的属性计算类条件概率更加容易操作,
需要注意的是:若某个属性值在训练集中和某个类别没有一起出现过,这样会抹掉其它的属性信息,因为该样本的类条件概率被计算为0。因此在估计概率值时,常常用进行平滑(smoothing)处理,拉普拉斯修正(Laplacian correction)就是其中的一种经典方法,具体计算方法如下
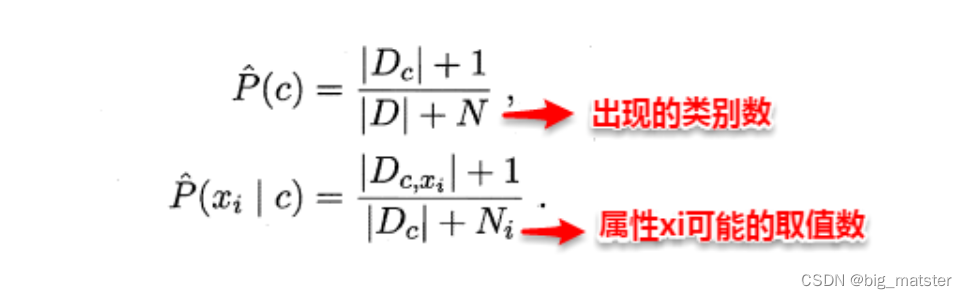
当训练集越大时,拉普拉斯修正引入的影响越来越小。对于贝叶斯分类器,模型的训练就是参数估计,因此可以事先将所有的概率储存好,当有新样本需要判定时,直接查表计算即可。
针对朴素贝叶斯,人们觉得它too sample,sometimes too naive!因此又提出了半朴素的贝叶斯分类器,具体有SPODE、TAN、贝叶斯网络等来刻画属性之间的依赖关系,此处不进行深入,等哪天和贝叶斯邂逅了再回来讨论。在此鼎鼎大名的贝叶斯介绍完毕,下一篇将介绍这一章剩下的内容--EM算法,朴素贝叶斯和EM算法同为数据挖掘的十大经典算法,想着还是单独介绍吧~
学习经验
看公式时候,慢慢地将公式手推导一遍,然后在将其他的公式算法及啥的都整理一般,全部都将其搞定都行啦的样子与打算。
版权归原作者 big_matster 所有, 如有侵权,请联系我们删除。