五年前深度学习的一切都是关于如何构建新的、更优化的模型,以便更好地从非结构化数据中学习。这些努力带来了许多研究突破,突破了神经网络的可能性。但慢慢地越来越多的人对这种方法提出了批评,并建议首先关注数据的质量和一致性。这些批评的声音通常来自行业,来自在关键业务环境中长时间大规模操作模型的专业人士。
在这篇文章中,我将对这两种方法提供一个新的视角。我将从统计的角度来看它们,看看它是否可以阐明哪种方法更好以及在什么情况下更好。
统计学有两个学派——频率派和贝叶斯派——它们与我们的主题有着有趣的相似之处。
- 在频率派中寻找概率 p(data|model),这意味着我们“假设”数据,“知道”模型。换句话说,模型是确定的(至少在工作目的上),但我们的不确定的测量,即数据,可能或可能不完美地反映模型(甚至现实)。
- 在贝叶斯方法中,我们寻找的概率是p(model|data),即我们“假设”模型,“知道”数据。我们的模型是不确定的,而数据是我们的基本事实——我们所知道的唯一确定的就是手头上的数据。
这些假设也导致了两种方法的不同重点。频繁主义者的方法涉及大量异常值、匹配方差和样本大小的概念,即它是以数据为中心的,不太关心模型。另一方面,贝叶斯方法是关于先验、可信度和抽样的,这意味着它们以模型为中心。为了理解这如何帮助我们更好的描述以模型为中心和以数据为中心的AI之间的区别,让我们先考虑一下统计学中最重要的方程:贝叶斯定理:
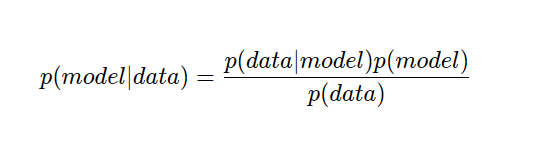
这意味着通过了解我们对模型(即 p(model) )和数据(即 p(data) )的确定性,我们可以合并这两个看似相反的观点。还有就是细节决定成败,这些无条件的概率在实践中会引起很多问题,我们下面继续讨论
归纳偏差和以模型为中心的AI
我们取p(model),它是一个特定模型拟合未来数据点的概率。如果它很高,那意味着我们相信有一个很好的数据模型。最大化这个概率的一个策略是在模型中加入一些归纳偏差。归纳偏差基本上是研究者关于问题空间的先验知识的某种升华。这就是为什么在以模型为中心的AI中我们喜欢:
- 引入受生物启发的架构(例如卷积滤波器)
- 定义复杂/复合损失函数(例如感知损失)
- 在超参数的可行范围内尝试网格/随机搜索
这些实际上是非常强大的方法。但这里有一个很大的问题:归纳偏差(不管它是否有用)仍然是一种偏差。
当选择一个特定的架构时,也限制了从数据中学到的东西。但是我们有时是喜欢这样做的,因为:
(1)我们知道数据中有某种噪声(即任务无关方差)和/或
(2)我们没有足够的数据来学习任何任意函数。
所以我们提出了两种主要的缓解措施:
(1)添加更多的数据,这样就可以训练更复杂的模型。
(2)将问题分解成步骤,并为它们训练单独的模型。
研究人员观察到的一件重要的事情是,添加的数据越多所需的归纳偏差就越少。例如,对试图学习的领域,transformer只需要很小的归纳偏差,但是却需要更大的数据(还记得VIT吗)。实际上,我们总是希望尽可能少地使用归纳偏差,因为我们希望AI系统解决的大多数任务都不容易创建先验模型(想象一下围棋或蛋白质折叠)。当我们没有正确的模型架构来完成任务时,无论如何高效地寻找超参数,都将以低于标准的性能结束。
贝叶斯模型也存在同样的问题。一些模型超参数与数据的拟合较好,但只要“正确”的模型没有包含在初始集中,“更好的拟合”在客观上仍然可能是非常糟糕的。
以数据为中心的AI
以数据为中心的人工智能不仅得到那些能够访问大量数据的人的支持,并且一般人们也都会认为训练数据越多越好。为了理解为什么会这样,让我们回到贝叶斯定理。我们在方程中得到的除数p(data)也被称为证据概率
在此先简单解释一下几个主要的概念:
在上式中,P(model|data)是后验概率(Posterior)
P(data|model)是似然(Likelihood)
P(model)是先验概率(Prior)
P(data)是证据(Evidence)
为什么给这几个概率取这么个名字呢?
在贝叶斯方法中,我们“知道”数据,“假设”模型
先验概率(Prior):在观测到data后,model是未知的。我们的目标是算出它是model的概率,而我们在观测之前已经知道了data是model的概率,因此P(model)叫做先验概率。
后验概率(Posterior):在观测到data后,知道data的信息后,model的概率就改变了。因为这个概率P(model|data)是在观测之后才知道的,所以叫做后验概率
证据(Evidence):因为我们已经知道data,并且已经观察到了这个事实的发生,因此对我们来说它是一个证据,而我们观察到这个证据的概率P(data)就叫证据
似然(Likelihood):字典上意思是一件事发生的可能性或概率,在这个例子中它表示当data是model时,它是data的概率。
这些概率有这些名字的根本原因是事件的发生顺序(发生在观测之前或之后)不同。
这听起来有点晦涩难懂,并且在许多现实场景中,要知道潜在的分布p(data)是很困难因为我们愿意相信我们得到的数据是在从潜在的分布中采样的,但实际上却是在异常值和/或通带有噪声的测量“设备”进行采样的。
因此,在以模型为中心的方法中,试图完全避免处理这个问题。在典型的拟合优度度量(贝叶斯因子、似然比等)中,我们只是提出证据概率。这就是为什么这些衡量标准总是比率的原因,也就是说它们只能判断一个模型是否比另一个更好。
但对于任何现实生活中的应用(例如,客户流失预测),我们对“最好”模型的相对好坏不感兴趣,而是对它的泛化感兴趣(例如,避免客户流失)。因此在以数据为中心的人工智能方法中,是希望致力于提高对p(data)的知识的归纳和总结。所以就想出了很多可以使用的方法:
- 监控数据质量以控制数据中的噪声和倾斜
- 进行更多的预处理,以减轻训练和线上推理时异常值的影响
- 用不同的模型处理不同的数据子集,提高了系统的整体性能
这些方法非常重要,尤其是在刚开始开发人工智能产品时。我们最终得到的是一个经过训练的模型,该模型的模型架构和超参数可以满足对收集到的数据进行建模并获得结果。
我曾参与过许多新开发的深度学习项目,每一次我看到的最大改进都来自于数据清理。但是清理数据不仅意味着要处理异常值、缺失值和重复值,还意味着要验证标注的一致性。有了更干净的数据,就可以从p(data)中进行更好的抽样,也就是说可以使用不同的数据增强技术对潜在的例子进行更彻底的抽样。
选择哪一个
一般·的文章会在结尾都会告诉你:成年人是不做选择题的,我全都要:使用归纳偏见和清理数据。但我想说的是,同时以这两个为中心是不太可能的,因为两者兼顾的问题在于,如果你不选则一个为中心,另外一个为辅助的话,而是最终会什么都得不到。在实践中,对数据和模型的同时改进会导致不明确的结果。例如一个项目经过一周的更改之后,终于看到了改进效果。但你应该把它归因于什么呢?是因为清理数据的工作吗?还是因为在模型架构上的工作?是两者的结合吗?你还是只能猜测。而且当看不到改进时,情况甚至更加困难:应该放弃该架构吗?更换数据处理方法?还是你不应该把它们放在一起同时使用?

这个例子虽然有一些夸张,但却是一个很好的实践:保持一切不变,只修改一个自变量,看看它对结果的影响。因此,在修改时不是从各个方面并行进行更改,而是以更结构化的方式解决问题:迭代。首先以数据为中心是肯定的,数据达到良好的一致性质量,再专注于增加模型的复杂性(无论是纯粹的参数数量还是归纳偏差的类型)。在进行项目时要坚持对照比较。需要管理的不仅是超参数和模型,而且还需要使用清晰的名称标记数据集的不同版本,这样才可以更清晰的查看哪些更改导致了哪些改进,所以使用git进行版本管理是一个非常好方法。
作者:Ágoston Török