本篇文章将介绍钟形曲线是如何形成的,以及π为什么会出现在一个看似与它无关的曲线的公式中。
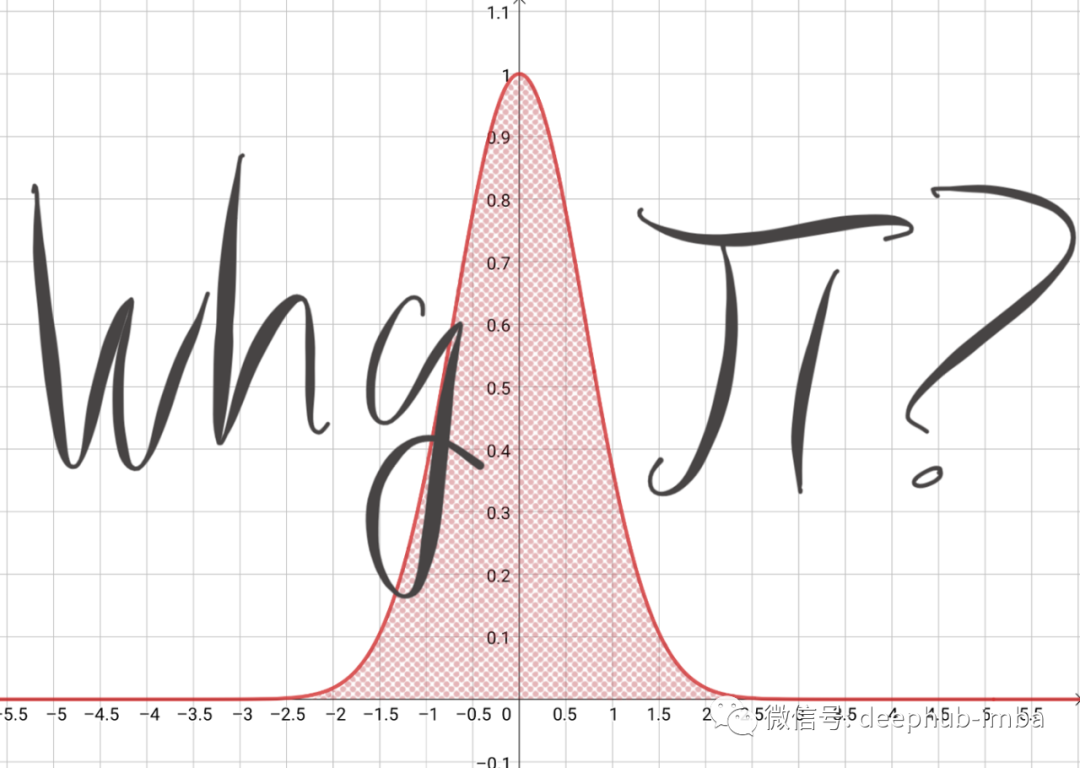
最近在翻阅一本旧的统计教科书时我发现了一个熟悉的正态分布方程:
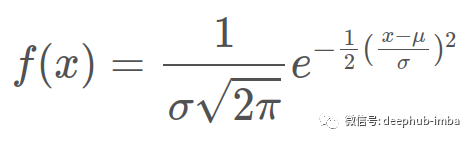
任何在大学上过统计学课程的人都遇到过这个等式。我自己也看过很多次了,但这次重新看,立刻想到了两个问题:
- 这东西究竟是如何形成正态分布的?
- π在那里做什么?
第一个问题似乎很简单也很容易弄清楚:我只需要学习方程产生的历史然后将其逐个拼凑起来。但第二个问题绝对让人感到困惑:正态分布的钟形曲线与圆有什么关系?在做了一些我自己的研究之后,我尝试通过这篇文章解释这种联系。
什么是钟形曲线?
在我们进入 π 部分之前,首先需要深入了解钟形曲线是如何形成的。首先从指数函数开始,我们可以在上面的等式中看到它。它是独立存在的:
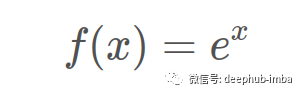
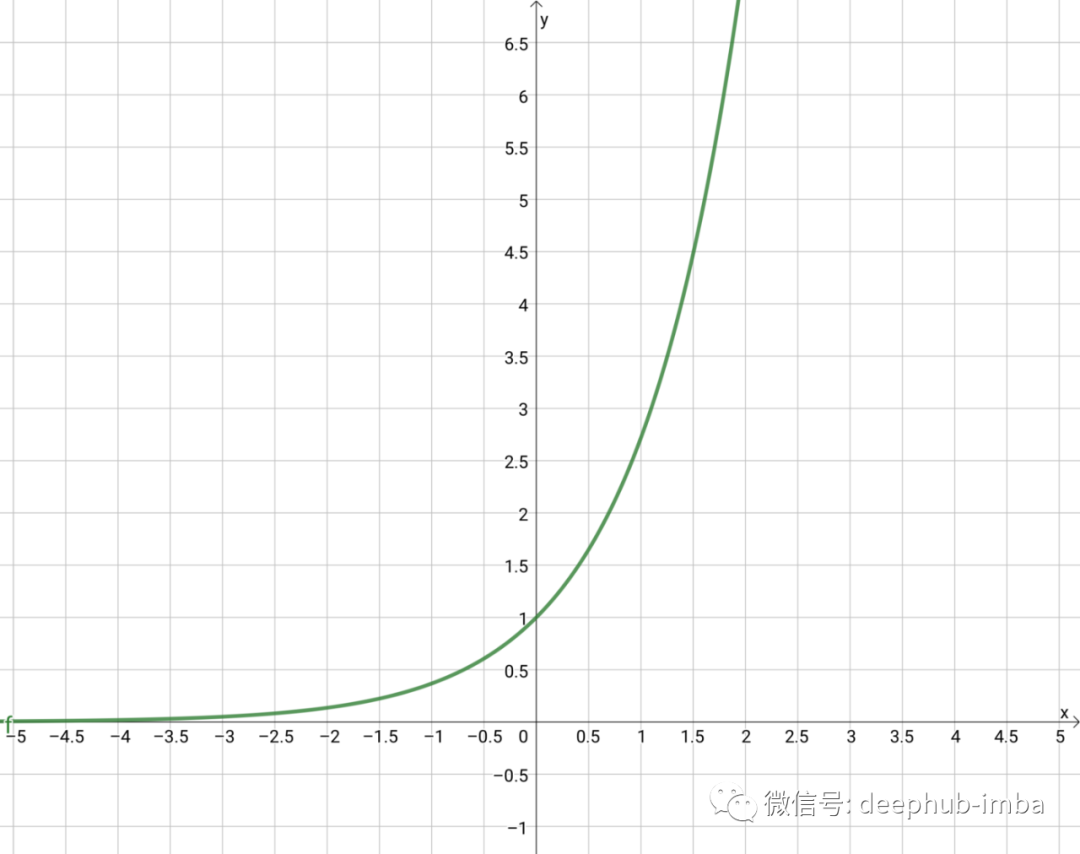
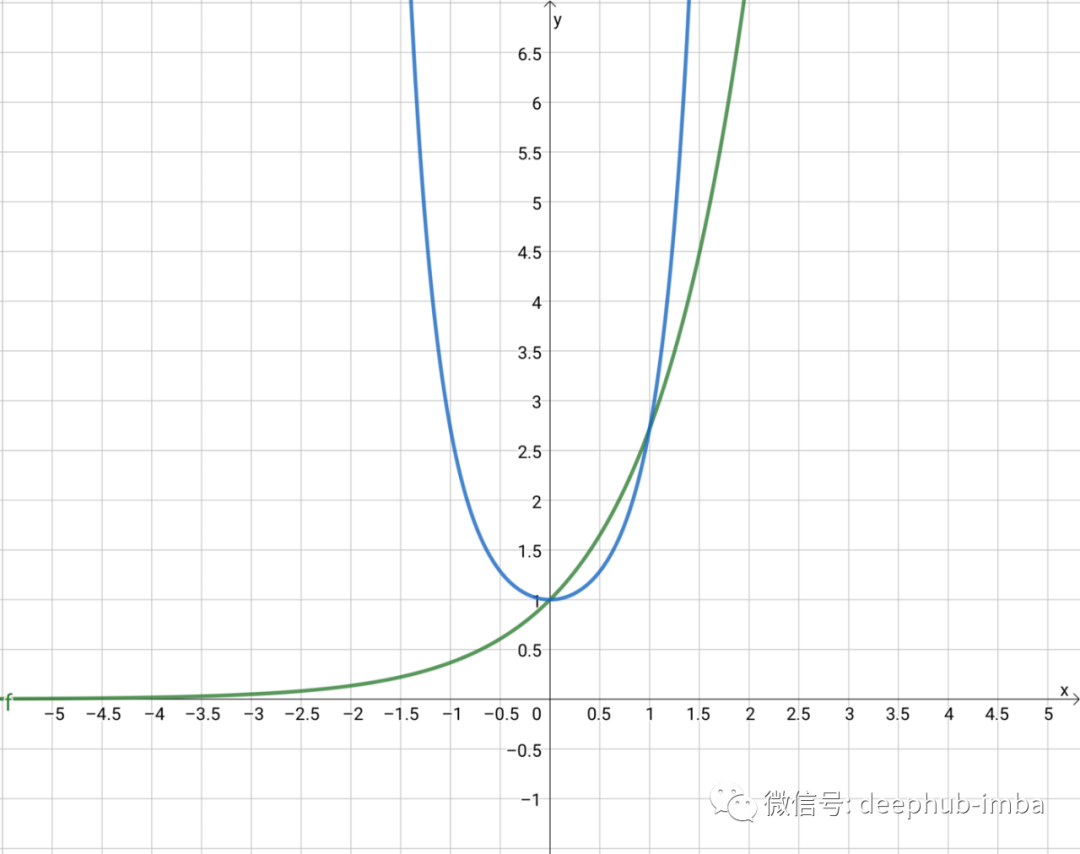
如果我们对 x 的值进行平方,它会变成看起来有点像二次方的东西,但实际上并不是二次方。相反,它是一个比二次函数增长得更快的函数,但具有一些相似的属性(例如关于其最低点对称)。将其添加到上面的图中进行比较,可以看到它们在 x=0 和 x=1 处具有相同的值:
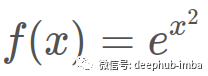
最后,让指数为负我们得到下面红色显示的钟形曲线:
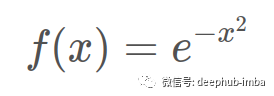
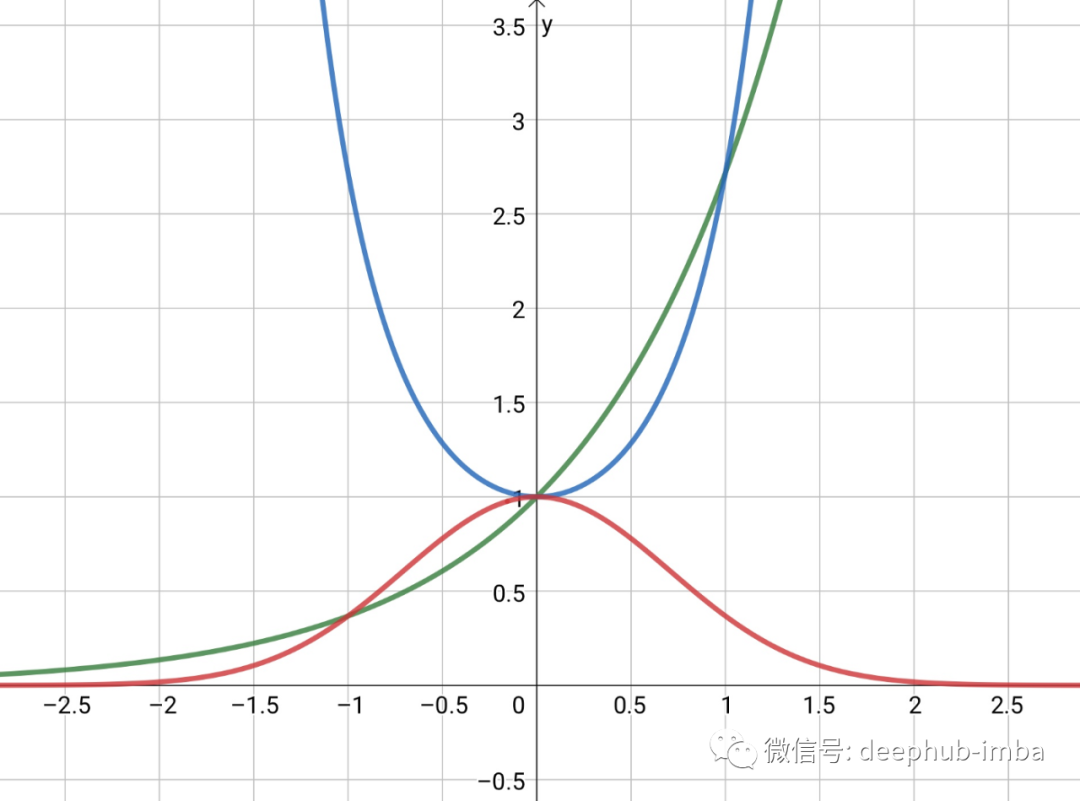
这个函数
f(x) = e^{-x²}
只是一个具有无限可能性的特殊钟形曲线,我们可以求e 的任意二次方。但是只有当二次曲线是凹的(也就是说它向下“打开”)时,才会得到钟形曲线。上面那个二次方是 -x²,它确实向下开。
例如,下面用蓝色绘制的方程 f(x) = x² + x + 2 不是凹的,当 e 取它时,你会得到绿色曲线,这显然不是钟形曲线:
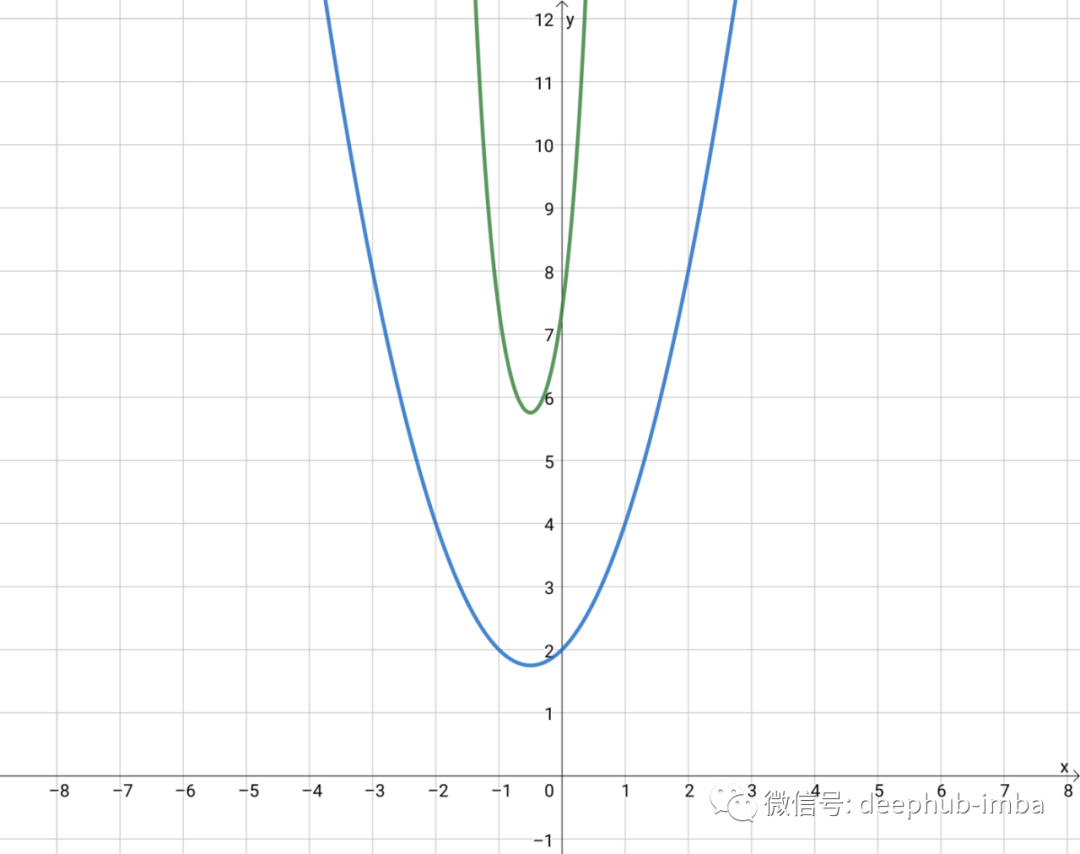
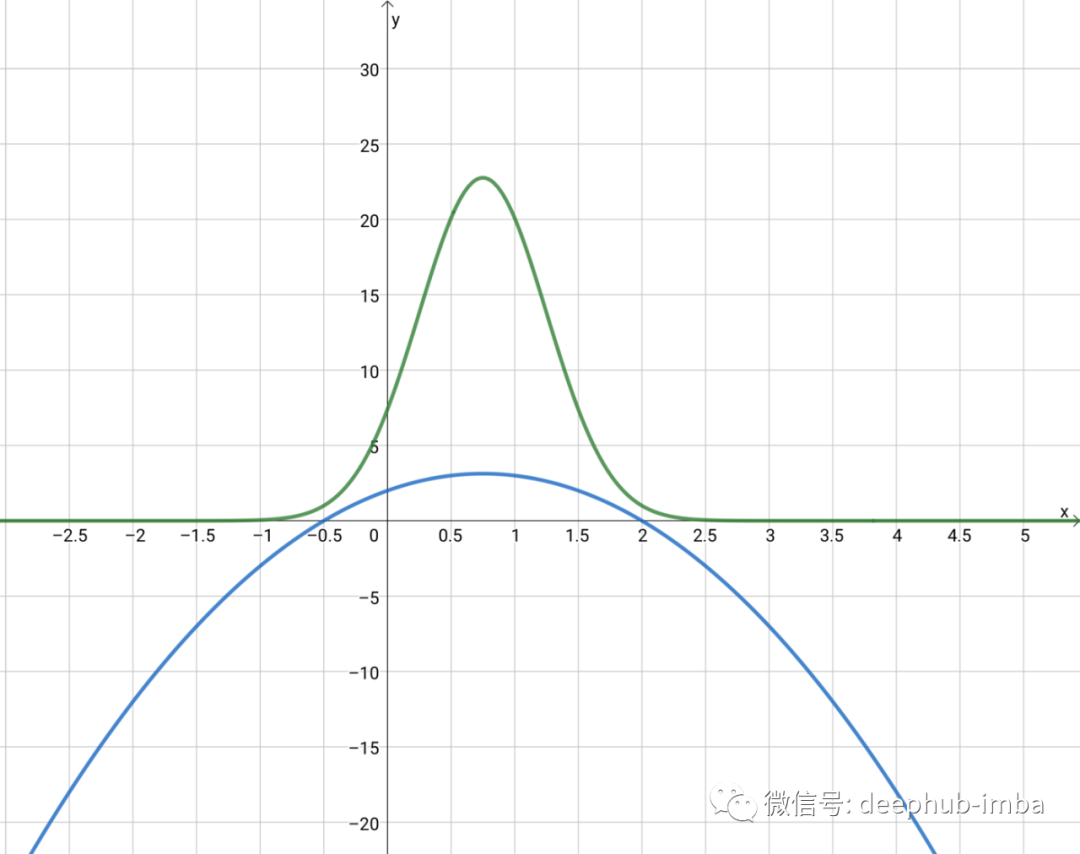
如果我们将等式转换为 f(x) = -2x² + 3x + 2,我们会得到一个凹函数,并且 e 形成钟形曲线的形状:
钟形曲线方程的一般方程被提升为二次方程:
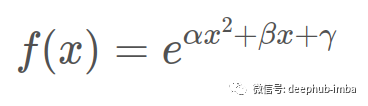
为了将其限制为凹二次方程,可以执行以下替换:
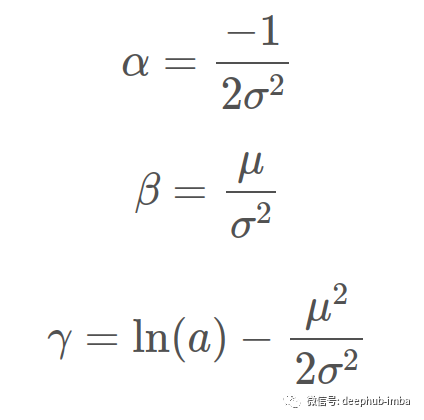
将这些代入并重新排列后得到以下结果,这几乎与我们在顶部开始的等式完全相同,只是在其前面加了一个 a:
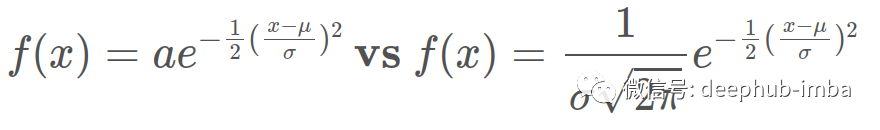
将a替换成右边的等式中的包含π 项的分数后,无论钟形曲线是什么形状,其下方的面积始终恰好为 1。这是因为对于统计分布:1 相当于 100% 的可能结果,并且面积总和应为该值。
换句话说,钟形曲线和那个 π 项之间的联系必须与曲线本身的面积有关。但这种联系究竟是什么?
Pi 与钟形曲线的关系
让我们回顾一下上面的工作。我们取了一个超越数 e,并将它提升到二次幂。当我们计算该曲线下的面积时,我们会得到另一个超越数 π。
事实证明这两个数字在几个方面是相关的,包括它们在复数系统中通过数学中最漂亮的方程之一的关系:e^{iπ} + 1 = 0。虽然这个等式在这里并没有被用到。
相反,正如我们将看到的π的出现让我们不得不去计算面积。我们可以通过计算e^{-x²}的平方,然后求平方根来得到这个面积。也就是说:
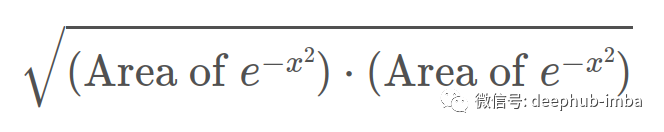
我们这么做的原因是我们需要用到微积分技巧来求面积。网上有很多例子可以说明如何做到这一点,但我想要提供的是这些分析解决方案不一定能传达的直观想法。
由于我们用来计算面积的变量是任意的,我们可以像下面这样简单地表示上面的方程,我们用y代替第二个x:
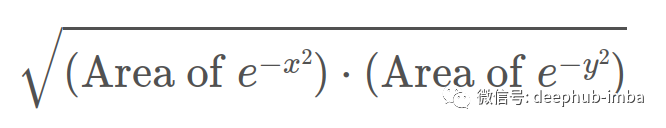
你现在可以把它想象成把一条钟形曲线放在x轴上另一条放在y轴上,然后获取它们的所有高度组合并绘制成三维图形:
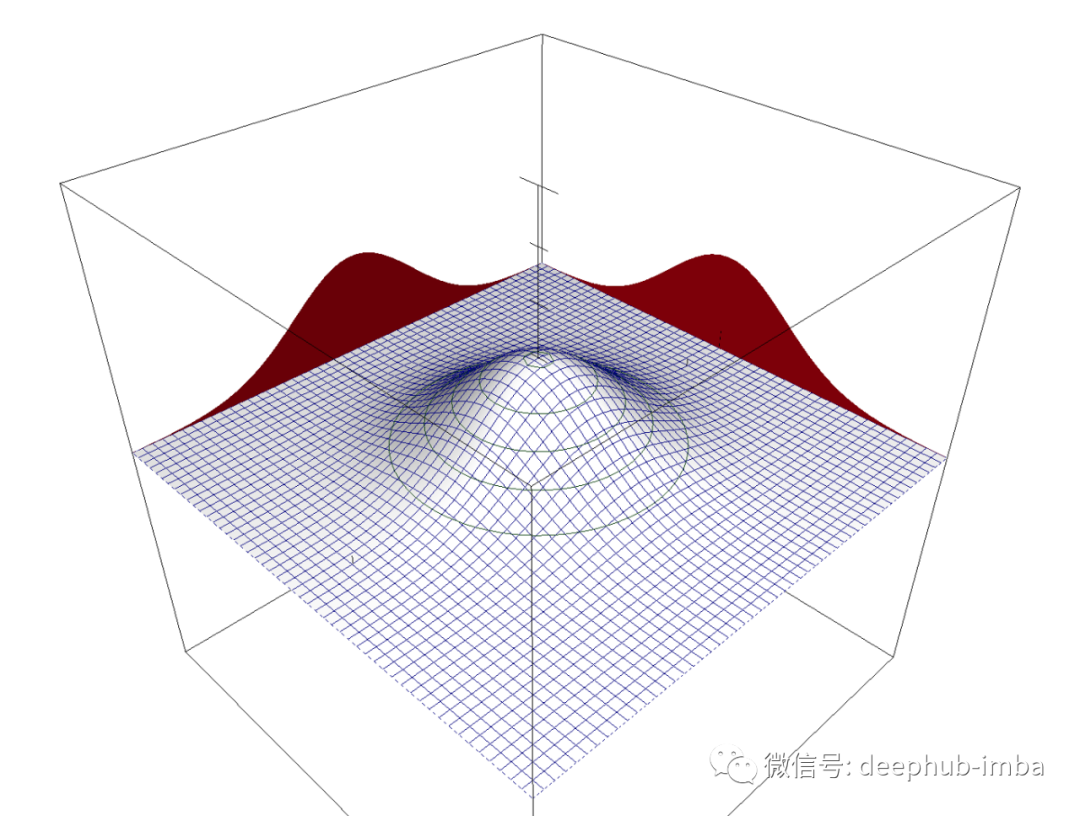
要获得其中一条曲线的面积,只需要获得形成的“山丘”的体积,然后取该值的平方根。与此类似的是,在维数较少的情况下,知道正方形的面积,然后通过开平方根得到它的边长。
这个技巧并不适用于所有类型的函数。如果二次方程(比如-x²+ 9),不会得到正确的答案。原因是这只适用于平方的旋转对称的函数。而高斯曲线,可以从下面类似的二次方程式图中看到它是“四方形的”并且不像上面的曲线那样通过旋转而对称。

但是如何得到体积呢?一种方法是将山坡分成像上面一样的正方形,然后在正方形中间获取每个正方形的高度。然后将这些方块的体积计算为(每个正方形的面积)⋅(高度),然后将所有这些较小的体积相加。正方形越小,近似效果越好(经典的微积分的思想)。
但是这样就隐藏了π是从哪里来的。如果我们不使用平方,而是将其径向划分。在这张图中,我们从山顶往下看,可以看到山的等高线:

把山顶划分成用黑色虚线表示的“片”。这些切片被进一步分割成蓝色突出显示的部分。将这些蓝色部分的面积乘以该点的山的高度,就得到体积:
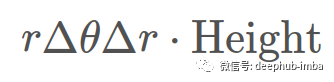
在这种情况下沿着“切片”重复此操作就可以得到整个切片的体积,然后将其乘以切片的总数就能获得整个体积。
如果让角度𝜃足够小那么它仅仅是一个薄片,可以将一片切片的体积乘以2π弧度(即圆中的弧度数)。
如果做这个数学运算(还是微积分),你会发现每个切片的面积正好是 0.5。将其乘以 2π 弧度,您将得到一个完全等于 π 的体积。
所以Pi来自于我们通过制作径向切片,然后将它们缝合成一个圆来得到体积。
总结
事实证明,任何通过旋转对称的东西都可以被认为与圆有关,圆意味着π肯定会潜藏在数学的某个地方。
虽然这不是一个严格的证明并且我跳过了很多细节(例如,两条钟形曲线的 3D 绘图通常不适用于所有函数,但它适用于我们使用的函数)。我希望这篇文章可以让你直观地理解为什么 π 似乎突然出现在与它无关的曲线的公式中。
作者:Ryan Brideau