《从零深入理解Yolo系列v1-v8全家桶 + 目标检测面试提问》
从零深入理解Yolo系列理论v1-v8
好玩的chatgpt网站
总结几个好玩。
Stable Diffusion 准确绘制人物动作及手脚细节(需ControlNet扩展)
目前AI绘图还是比较像开盲盒,虽然能根据语义提供惊艳的图片,但是与设计师所构思的目标还是有一定距离。那像我们这种没有绘画功底的程序员想要制作出心中的人物(尤其手脚)姿态,该怎样减少随机开盒的次数呢?本文提供几种精确控制人物动作的方法,从易到繁,从粗到细,其中方法四是。注意:正式使用前请先确认你的St
Lesson 10.1 超参数优化与枚举网格的理论极限和随机网格搜索 RandomSearchCV
【代码】Lesson 10.1 超参数优化与枚举网格的理论极限和随机网格搜索 RandomSearchCV。
b站B导的yoloV7版本添加注意力机制
yolov7增加注意力机制(b导版本)
为什么我们认为GPT是一个技术爆炸
为什么我们认为GPT是一个技术爆炸
抱抱脸:ChatGPT背后的算法——RLHF | 附12篇RLHF必刷论文
文 | 卖萌酱大家好,我是卖萌酱。前几天,抱抱脸公司(HuggingFace)发表了一篇博客[1],详细讲解了ChatGPT背后的技术原理——RLHF。笔者读过之后,觉得讲解的还是蛮清晰的,因此提炼了一下核心脉络,希望给对ChatGPT技术原理感兴趣的小伙伴带来帮助。此外,文末整理了几篇关于 RLH
本地生成动漫风格 AI 绘画 图像|Stable Diffusion WebUI 的安装和局域网部署教程
先放一张WebUI的图片生成效果图对比,以给大家学习的动力 :)怎么样,有没有小小的心动?这里再补充一下,是可以生成的图片的。
微信小程序 |做一款跟ChatGPT下五指棋的小程序
本文基于ChatGPT的语言理解能力,结合时下流行的uniapp框架以及轻量级web框架Flask,从前端到后端,全栈搭建了一个能和chatGPT 这个AI模型进行实时下棋的小程序。项目完整,功能丰富,极力推荐学习!
如何搭建chatGPT4.0模型-国内如何用chatGPT4.0
在国内,目前可以通过以下途径使用 OpenAI 的 ChatGPT 4.0:自己搭建模型:如果您具备一定的技术能力,可以通过下载预训练模型和相关的开发工具包,自行搭建 ChatGPT 4.0 模型。OpenAI提供了相关的软件开发工具,包括Python API,也有为一些主流应用框架提供可用的API
第十一届泰迪杯数据挖掘挑战赛-产品订单数据分析B题(完整代码)--数据处理--第一部分(下一部分请看下一博客)
第十一届泰迪杯数据挖掘挑战赛-B题,数据处理以及特征序列增加
使用lidar_align进行激光雷达与IMU的外参标定(超详细教程)
使用lidar_align进行激光雷达与IMU的外参标定(超详细教程),安装lidar_align编译可能遇到的问题解决
Transformer模型入门详解及代码实现
本文对Transformer模型的基本原理做了入门级的介绍,意在为读者描述整体思路,而并非拘泥于细微处的原理剖析,并附上了基于PYTORCH实现的Transformer模型代码及详细讲解。
OpenCV实战——多尺度FAST特征检测
FAST 是用于快速检测图像中关键点的方法,而 SURF 和 SIFT 算法的设计重点是尺度不变性。为了同时实现快速检测和尺度不变性,OpenCV 中引入了新的兴趣点检测器,包括 BRISK (Binary Robust Invariant Scalable Keypoints) 检测器(基于 FA
gpt保姆级注册教程
gpt的注册教程,帮大家整理好了。欢迎大家学习讨论gpt
Python调用GPT3.5接口的最新方法
GPT3.5接口调用方法主要包括openai安装、api_requestor.py替换、接口调用、示例程序说明四个部分。
ChatGPT镜像来了,体验核心能力
chatgpt怎么注册?chatgpt国内镜像
指纹识别综述(4): 指纹匹配
介绍刑侦、手机解锁、身份证管理等各种身份识别应用中的各类指纹匹配技术,包括细节点匹配、深度学习匹配技术、指纹绝对对齐、指纹刚性和弹性配准等。
local_rank,rank,node等理解
node,rank,local_rank
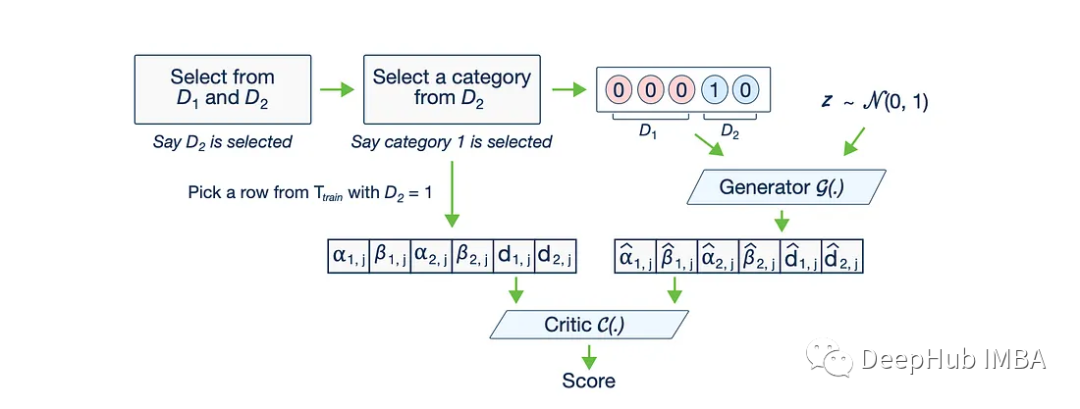
用CTGAN生成真实世界的表格数据
随着CLIP和稳定模型的快速发展,图像生成领域中GAN已经不常见了,但是在表格数据中GAN还是可以看到它的身影。