线性判别分析法（LDA）

    在主成分分析法（PCA）中，我们对降维算法PCA做了总结。这里我们就对另外一种经典的降维方法线性判别分析（Linear Discriminant Analysis, 以下简称LDA）做一个总结。LDA在模式识别领域（比如人脸识别，舰艇识别等图形图像识别领域）中有非常广泛的应用，因此我们有必要了解下它的算法原理。

　　　　在学习LDA之前，有必要将其自然语言处理领域的LDA区别开来，在自然语言处理领域， LDA是隐含狄利克雷分布（Latent Dirichlet Allocation，简称LDA），他是一种处理文档的主题模型。我们本文只讨论线性判别分析，因此后面所有的LDA均指线性判别分析。

一、LDA思想

    LDA属于机器学习中的监督学习算法，常用来做特征提取、数据降维和任务分类。LDA算法与PCA算法都是常用的降维技术。**两者最大的区别在于：LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的；而PCA是不考虑样本类别输出的无监督降维技术**。LDA的思想可以用一句话概括：“**投影后类内方差最小，类间方差最大**”（即我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。）

    可能还是有点抽象，我们先看看最简单的情况。假设我们有两类数据分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

    上图中提供的两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好，因为右图的红色数据和蓝色数据各点之间较为集中，且两个类别之间的距离明显。左图则在边界处数据混杂。

    当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。 

二、LDA算法原理

    在我们将上面直观的内容转化为可以度量的问题之前，我们先了解些必要的数学基础知识，这些在后面讲解具体LDA原理时会用到。

（一）瑞利商和广义瑞利商

1、瑞利商

我们首先来看看瑞利商的定义。瑞利商是指这样的函数R(A,x):

2、广义瑞利商

广义瑞利商是指这样的函数R(A,B,x):

（二）二类LDA原理

    现在我们回到LDA的原理上，我们在第一节说讲到了LDA希望投影后希望同一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大，但是这只是一个感官的度量。现在我们首先从比较简单的二类LDA入手，严谨的分析LDA的原理。 

（三）多类LDA原理

三、LDA算法流程

    以上就是使用LDA进行降维的算法流程。实际上LDA除了可以用于降维以外，还可以用于分类。一个常见的LDA分类基本思想是假设各个类别的样本数据符合高斯分布，这样利用LDA进行投影后，可以利用极大似然估计计算各个类别投影数据的均值和方差，进而得到该类别高斯分布的概率密度函数。当一个新的样本到来后，我们可以将它投影，然后将投影后的样本特征分别带入各个类别的高斯分布概率密度函数，计算它属于这个类别的概率，最大的概率对应的类别即为预测类别。

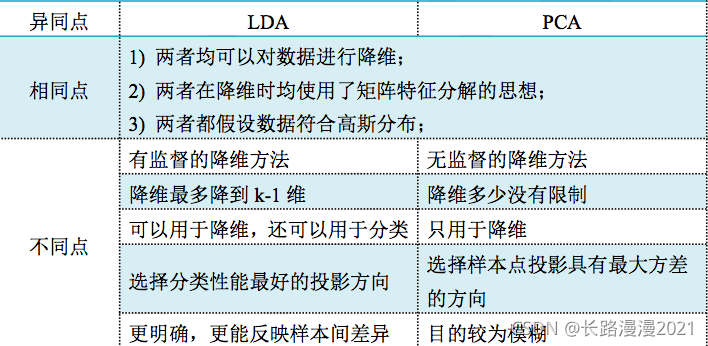
四、LDA与PCA比较

（一）LDA vs PCA

    LDA用于降维，和PCA有很多相同，也有很多不同的地方，因此值得好好的比较一下两者的降维异同点。

（二）用scikit-learn分别对PCA和LDA进行比较

1、对scikit-learn中LDA类概述

    在scikit-learn中， LDA类是sklearn.discriminant_analysis.LinearDiscriminantAnalysis。那既可以用于分类又可以用于降维。当然，应用场景最多的还是降维。和PCA类似，LDA降维基本也不用调参，只需要指定降维到的维数即可。

2、降维实例

    在前面我们讲到，PCA和LDA都可以用于降维。两者没有绝对的优劣之分，使用两者的原则实际取决于数据的分布。由于LDA可以利用类别信息，因此某些时候比完全无监督的PCA会更好。下面我们举一个LDA降维可能更优的例子。 

我们首先生成三类三维特征的数据，代码如下：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_blobs, make_classification
# 生成三类三维特征的数据
X, y = make_classification(n_samples=1000, n_features=3, n_redundant=0, n_classes=3, n_informative=2,
                           n_clusters_per_class=1, class_sep=0.5, random_state=10)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker='o', c=y)
plt.show()

我们看看最初的三维数据的分布情况：

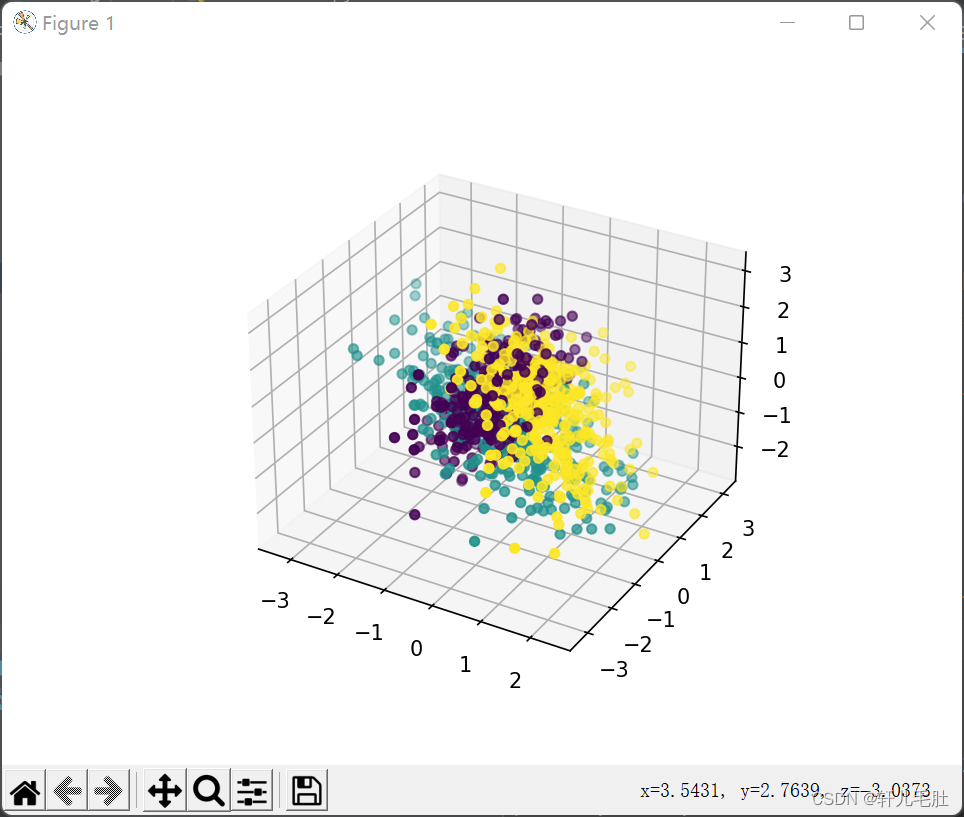
首先我们看看使用PCA降维到二维的情况，注意PCA无法使用类别信息来降维，代码如下：

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
X_new = pca.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1], marker='o', c=y)
plt.show()

在输出中，PCA找到的两个主成分方差比和方差如下：

[0.43377069 0.3716351 ]
[1.21083449 1.0373882 ]

输出的降维效果图如下:

由于PCA没有利用类别信息，我们可以看到降维后，样本特征和类别的信息关联几乎完全丢失。

现在我们再看看使用LDA的效果，代码如下：

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X, y)
X_new = lda.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1], marker='o', c=y)
plt.show()

我们这里对LinearDiscriminantAnalysis类的参数做一个基本的总结。

1.参数解释
solver：字符串，可选参数。指定求解超平面矩阵的方法。可选方法有
(1) ‘svd’：奇异值分解(默认)。不需要计算协方差矩阵，因此对于具有大规模特征的数据，推荐使用该方法，该方法既可用于分类也可用于降维。
(2) ‘lsqr’：最小二乘，结合shrinkage参数。该方法仅可用于分类。
(3) ‘eigen’：特征值分解，结合shrinkage参数。特征值不多的时候推荐使用该方法，该方法既可用于分类也可用于降维。

shrinkage：字符串或者浮点数，可选参数。正则化参数，增强LDA分类的泛化能力(仅做降维时可不考虑此参数)。
(1) None：不正则化(默认)。
(2) ‘auto’：算法自动决定是否正则化。
(3) [0,1]之间的浮点数：指定值。

shrinkage参数仅在solver参数选择’lsqr’和’eigen’时有用。

priors：数组，可选参数。数组中的元素依次指定了每个类别的先验概率，默认为None，即每个类相等。降维时一般不需要关注这个参数。

n_components：整数，可选参数。指定降维时降到的维度，该整数必须小于等于min(分类类别数-1，特征数)，默认为None，即min(分类类别数-1，特征数)。

store_covariance：布尔值，可选参数。额外计算每个类别的协方差矩阵，仅在solver参数选择’svd’时有效，默认为False不计算。

tol：浮点数，可选参数。指定’svd’中秩估计的阈值。默认值为0.0001。

2.属性解释
coef_：数组，shape (特征数,) or (分类数, 特征数)。权重向量。
intercept_：数组，shape (特征数,) 。截距项。
covariance_：数组，shape (特征数, 特征数) 。适用于所有类别的协方差矩阵。
explained_variance_ratio_：数组，shape (n_components,) 。每一个维度解释的方差占比(原文Percentage of variance explained by each of the selected components)。
means_：数组，shape (分类数, 特征数) 。类均值。
priors_：数组，shape (分类数,) 。类先验概率(加起来等于1)。
scalings_：数组，shape (rank秩, 分类数-1) 。每个高斯分布的方差σ(原文Scaling of the features in the space spanned by the class centroids)。
xbar_：数组，shape (特征数,) 。整体均值。
classes_：数组，shape (分类数,) 。去重的分类标签Unique class labels，即分哪几类。

3.方法解释
decision_function(self, X)：
预测置信度分数。置信度分数是样本到（分类）超平面的带符号的距离。
参数： X: shape(样本数量, 特征数)
返回值：数组，二分类——shape(样本数,)，多分类——shape(样本数, 分类数)

fit(self, X, y)：
训练模型

fit_transform(self, X, y=None, **fit_params)：
训练模型同时将X转换为新维度的标准化数据。
参数：X,y
返回值：数组，shape(样本数量, 新特征数)

transform(self, X)：
X转换为标准化数据。
参数：X
返回值：数组，shape(样本数量, 维数)

get_params(self, deep=True)：
以字典返回LDA模型的参数值，比如solver、priors等。参数deep默认为True，还会返回包含的子模型的参数值。

predict(self, X)：
根据模型的训练，返回预测值。
参数：X: shape(样本数量, 特征数)
返回值：数组，shape [样本数]

score(self, X, y, sample_weight=None)：
根据给定的测试数据X和分类标签y返回预测正确的平均准确率。可以用于性能度量，返回模型的准确率，参数为x_test，y_test。
参数：X,y
返回值：浮点数

predict_log_proba(self, X)：
返回X中每一个样本预测为各个分类的对数概率
参数： X
返回值：数组，shape(样本数, 分类数)

predict_proba(self, X)：
返回X中每一个样本预测为各个分类的概率
参数： X
返回值：数组，shape(样本数, 分类数)

输出的效果图如下：

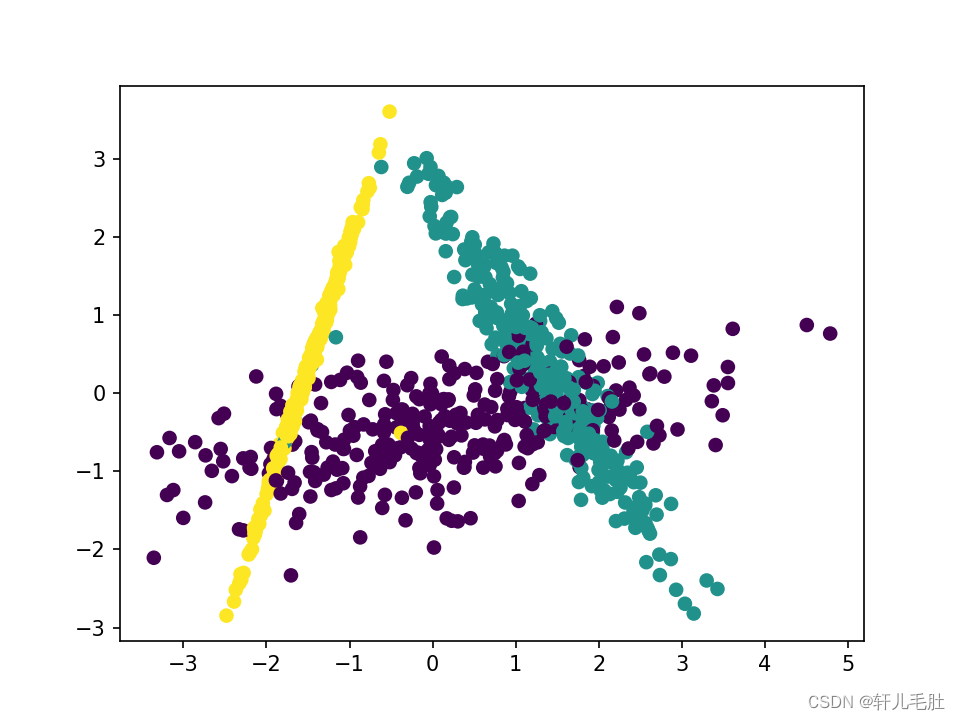
可以看出降维后样本特征和类别信息之间的关系得以保留。

一般来说，如果我们的数据是有类别标签的，那么优先选择LDA去尝试降维；当然也可以使用PCA做很小幅度的降维去消去噪声，然后再使用LDA降维。如果没有类别标签，那么肯定PCA是最先考虑的一个选择了。

五、LDA算法总结

     LDA算法既可以用来降维，又可以用来分类，但是目前来说，主要还是用于降维。在我们进行图像识别图像识别相关的数据分析时，LDA是一个有力的工具。下面总结下LDA算法的优缺点。

    LDA算法的主要优点有：

    LDA算法的主要缺点有： 

六、实例

（一）python实现

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

def LDA(data, target, n_dim):
    """
    :param data: (n_samples, n_features)
    :param target: data class
    :param n_dim: target dimension
    :return: (n_samples, n_dims)
     """
    clusters = np.unique(target)

    if n_dim > len(clusters) - 1:
        print("K is too much")
        print("please input again")
        exit(0)

    # within_class scatter matrix
    Sw = np.zeros((data.shape[1], data.shape[1]))
    for i in clusters:
        datai = data[target == i]
        datai = datai - datai.mean(0)
        Swi = np.mat(datai).T * np.mat(datai)
        Sw += Swi

    # between_class scatter matrix
    SB = np.zeros((data.shape[1], data.shape[1]))
    u = data.mean(0)  # 所有样本的平均值
    for i in clusters:
        Ni = data[target == i].shape[0]
        ui = data[target == i].mean(0)  # 某个类别的平均值
        SBi = Ni * np.mat(ui - u).T * np.mat(ui - u)
        SB += SBi
    S = np.linalg.inv(Sw) * SB
    eigVals, eigVects = np.linalg.eig(S)  # 求特征值，特征向量
    eigValInd = np.argsort(eigVals)
    eigValInd = eigValInd[:(-n_dim - 1):-1]
    w = eigVects[:, eigValInd]
    data_ndim = np.dot(data, w)

    return data_ndim

if __name__ == '__main__':
    iris = load_iris()
    X = iris.data
    Y = iris.target
    target_names = iris.target_names
    X_r2 = LDA(X, Y, 2)
    colors = ['navy', 'turquoise', 'darkorange']

    for color, i, target_name in zip(colors, [0, 1, 2], target_names):
        plt.scatter(X_r2[Y == i, 0], X_r2[Y == i, 1], alpha=.8, color=color,
                    label=target_name)
    plt.legend(loc='best', shadow=False, scatterpoints=1)
    plt.title('LDA of IRIS dataset by Python')

    plt.show()

（二）sklearn实现

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

iris = datasets.load_iris()
X = iris.data
Y = iris.target
target_names = iris.target_names
lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, Y).transform(X)
colors = ['navy', 'turquoise', 'darkorange']

for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(X_r2[Y == i, 0], X_r2[Y == i, 1], alpha=.8, color=color,
                label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA of IRIS dataset by sklearn')

plt.show()

（三）LDA实现iris 数据

首先，iris数据集可以去该博主的GitHub下载

下面我们分析导入的数据集，代码如下：

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.preprocessing import LabelEncoder
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

feature_dict = {i: label for i, label in zip(range(4), ("Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width",))}
# print(feature_dict)  # {0: 'Sepal.Length', 1: 'Sepal.Width', 2: 'Petal.Length', 3: 'Petal.Width'}

df = pd.read_csv('iris.csv', sep=',')
df.columns = ["Number"] + [l for i, l in sorted(feature_dict.items())] + ['Species']
# to drop the empty line at file-end
df.dropna(how='all', inplace=True)
# print(df.tail())  # 打印数据的后五个，和 .head() 是对应的

下面我们把数据分成data和label，如下形式：

X = df[["Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width"]].values
y = df['Species'].values
enc = LabelEncoder()
label_encoder = enc.fit(y)
y = label_encoder.transform(y) + 1

这样我们对label进行分类，其中{1: 'Setosa', 2: 'Versicolor', 3: 'Virginica'}，分类大概是这样的：

label_dict = {1: 'setosa', 2: 'versicolor', 3: 'virginica'}

下面我们分别求三种鸢尾花数据在不同特征维度上的均值向量 Mi。

求均值的代码如下：

np.set_printoptions(precision=4)
mean_vectors = []
for c1 in range(1, 4):
    mean_vectors.append(np.mean(X[y == c1], axis=0))
    print('Mean Vector class %s : %s\n' % (c1, mean_vectors[c1 - 1]))

三个类别，求出的均值如下：

下面计算两个 4*4 维矩阵：类内散布矩阵和类间散布矩阵

类内散度矩阵公式如下：

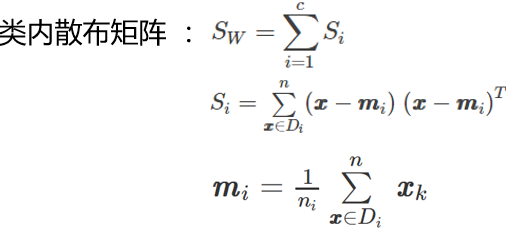
代码如下：

S_W = np.zeros((4, 4))
for c1, mv in zip(range(1, 4), mean_vectors):
    # scatter matrix for every class
    class_sc_mat = np.zeros((4, 4))
    for row in X[y == c1]:
        # make column vectors
        row, mv = row.reshape(4, 1), mv.reshape(4, 1)
        class_sc_mat += (row - mv).dot((row - mv).T)
    # sum class scatter metrices
    S_W += class_sc_mat
 print('within-class Scatter Matrix:\n', S_W)

结果如下：

1

2

3

4

5

within-

class

Scatter Matrix:

[[38.9562 13.63   24.6246  5.645 ]

[13.63   16.962   8.1208  4.8084]

[24.6246  8.1208 27.2226  6.2718]

[ 5.645   4.8084  6.2718  6.1566]]

类间散布矩阵如下：

代码如下：

overall_mean = np.mean(X, axis=0)
S_B = np.zeros((4, 4))
for i, mean_vec in enumerate(mean_vectors):
    n = X[y == i + 1, :].shape[0]
    # make column vector
    mean_vec = mean_vec.reshape(4, 1)
    # make column vector
    overall_mean = overall_mean.reshape(4, 1)
    S_B += n * (mean_vec - overall_mean).dot((mean_vec - overall_mean).T)
print('between-class Scatter matrix:\n', S_B)

结果展示：

1

2

3

4

5

between-

class

Scatter matrix:

[[ 63.2121 -19.9527 165.2484  71.2793]

[-19.9527  11.3449 -57.2396 -22.9327]

[165.2484 -57.2396 437.1028 186.774 ]

[ 71.2793 -22.9327 186.774   80.4133]]

然后我们求解矩阵的特征值：

代码如下：

eig_vals, eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))

for i in range(len(eig_vals)):
    eigvec_sc = eig_vecs[:, i].reshape(4, 1)
    print('\n Eigenvector {}: \n {}'.format(i+1, eigvec_sc.real))
    print('Eigenvalue {: }: {:.2e}'.format(i+1, eig_vals[i].real))

结果如下：

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

Eigenvector 1:

[[ 0.2087]

[ 0.3862]

[-0.554 ]

[-0.7074]]

Eigenvalue  1: 3.22e+01

Eigenvector 2:

[[-0.0065]

[-0.5866]

[ 0.2526]

[-0.7695]]

Eigenvalue  2: 2.85e-01

Eigenvector 3:

[[-0.868 ]

[ 0.3515]

[ 0.3431]

[ 0.0729]]

Eigenvalue  3: -1.04e-15

Eigenvector 4:

[[-0.1504]

[-0.2822]

[-0.3554]

[ 0.8783]]

Eigenvalue  4: 1.16e-14

最后求特征值与特征向量，其中：

• 特征向量：表示映射方向
• 特征值：特征向量的重要程度

代码如下：

# make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:, i]) for i in range(len(eig_vals))]

# sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)

# Visually cinfirm that the list is correctly sorted by decreasing eigenvalues
print('Eigenvalues in decreasing order: \n')
for i in eig_pairs:
    print(i[0])

特征向量如下：

特征值代码如下：

print('Variance explained：\n')
eigv_sum = sum(eig_vals)
for i, j in enumerate(eig_pairs):
    print('eigenvalue {0:}: {1:.2%}'.format(i + 1, (j[0] / eigv_sum).real))

结果如下：

我们从上可以知道，选择前两维特征：

W = np.hstack((eig_pairs[0][1].reshape(4, 1), eig_pairs[1][1].reshape(4, 1)))
print('Matrix W: \n', W.real)

特征矩阵W如下：

lda如下：

X_lda = X.dot(W)
assert X_lda.shape == (150, 2), 'The matrix is not 150*2 dimensional.'

下面画图：

def plt_step_lda():
    ax = plt.subplot(111)
    for label, marker, color in zip(range(1, 4), ('^', 's', 'o'), ('blue', 'red', 'green')):
        plt.scatter(x=X_lda[:, 0].real[y == label],
                    y=X_lda[:, 1].real[y == label],
                    marker=marker,
                    color=color,
                    alpha=0.5,
                    label=label_dict[label])
    plt.xlabel('LD1')
    plt.ylabel('LD2')

    leg = plt.legend(loc='upper right', fancybox=True)
    leg.get_frame().set_alpha(0.5)
    plt.title('LDA: Iris projection onto the first 2 linear discriminants')

    # hide axis ticks
    plt.tick_params(axis='both', which='both', bottom='off',
                    top='off', labelbottom='on', left='off',
                    labelleft='on')

    # remove axis spines
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['left'].set_visible(False)

    plt.grid()
    plt.tight_layout()
    plt.show()

如图所示：

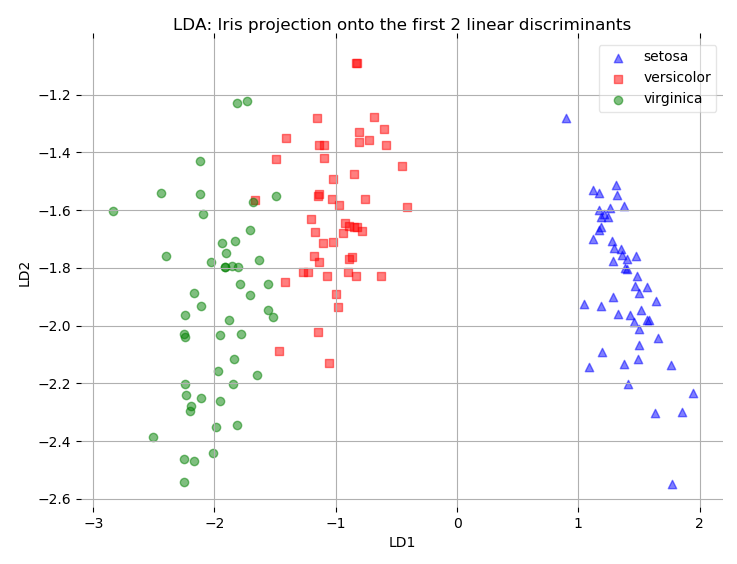
使用sklearn实现lda：

# LDA
sklearn_lda = LDA(n_components=2)
X_lda_sklearn = sklearn_lda.fit_transform(X, y)

def plot_scikit_lda(X, title):
    ax = plt.subplot(111)
    for label, marker, color in zip(range(1, 4), ('^', 's', 'o'), ('blue', 'red', 'green')):
        plt.scatter(x=X_lda[:, 0].real[y == label],
                    # flip the figure
                    y=X_lda[:, 1].real[y == label] * -1,
                    marker=marker,
                    color=color,
                    alpha=0.5,
                    label=label_dict[label])
    plt.xlabel('LD1')
    plt.ylabel('LD2')

    leg = plt.legend(loc='upper right', fancybox=True)
    leg.get_frame().set_alpha(0.5)
    plt.title(title)

    # hide axis ticks
    plt.tick_params(axis='both', which='both', bottom='off',
                    top='off', labelbottom='on', left='off',
                    labelleft='on')

    # remove axis spines
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['left'].set_visible(False)

    plt.grid()
    plt.tight_layout()
    plt.show()

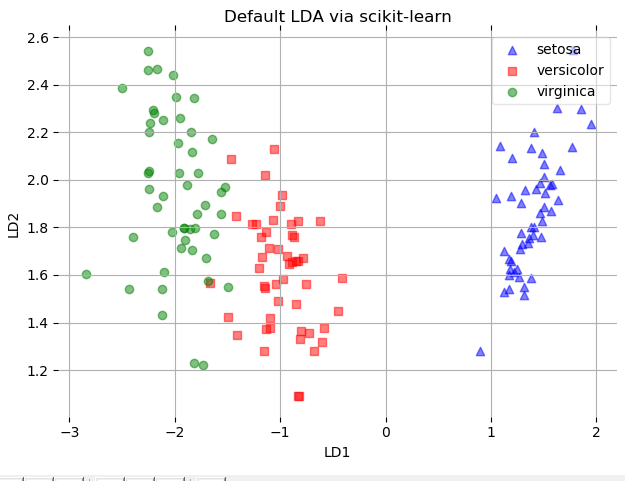
plot_scikit_lda(X, title='Default LDA via scikit-learn')

结果如下：

（四）手机价格分类实例

本例数据来源于机器学习竞赛平台Kaggle，一个关于手机价格分类的数据。数据地址：https://www.kaggle.com/iabhishekofficial/mobile-price-classification

数据一共2000个样例，20个字段。分类字段为price_range，一共分为了4类。数据集无缺失值，无错误值。字段及解释如下：

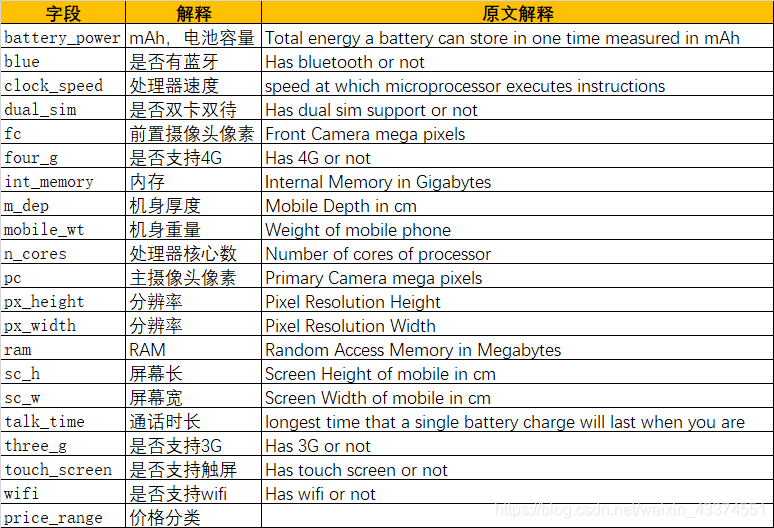由于从一般常识得知，机身厚度和机身重量对价格往往是没有直接影响的，故在建模时将这两个字段剔除。

import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn import model_selection

# 读取数据
data = pd.read_csv(r'C:\Users\Administrator\Desktop\train.csv')
# 剔除两个无关字段
data.drop(['m_dep', 'mobile_wt'], axis=1, inplace=True)
X = data[data.columns[:-1]]
Y = data[data.columns[-1]]
# 拆分为训练集和测试集
x_train, x_test, y_train, y_test = model_selection.train_test_split(X, Y, test_size=0.25, random_state=1234)
# LDA
lda = LinearDiscriminantAnalysis()
# 训练模型
lda.fit(x_train, y_train)
# 模型评估
print('模型准确率:\n', lda.score(x_test, y_test))

最终得到模型的准确率为94.8%，说明模型效果还是不错的。

参考文献：

1、线性判别分析LDA原理总结

2、用scikit-learn进行LDA降维

3、线性分类（二）-- 线性判别分析 LDA

4、Python机器学习笔记：线性判别分析（LDA）算法

5、机器学习算法理论与实践——线性判别分析(LDA)