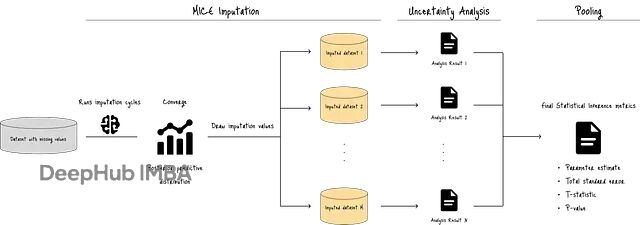
别再用均值填充了!MICE算法教你正确处理缺失数据
本文会通过PMM(Predictive Mean Matching)和线性回归等具体方法,拆解MICE的工作原理,同时对比标准回归插补作为参照。

12 种 Pandas 测试技巧,让数据处理少踩坑
下面这 12 个策略是实际项目里反复使用的测试方法,能让数据处理代码变得比较靠谱。
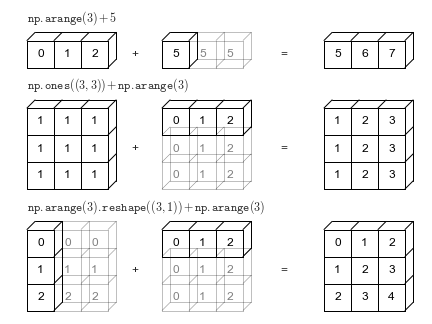
NumPy广播:12个技巧替代循环,让数组计算快40倍
广播是NumPy里最让人恍然大悟的特性。掌握后能去掉大量循环,让代码意图更清晰,同时获得向量化带来的性能提升——而且不需要引入什么复杂工具。
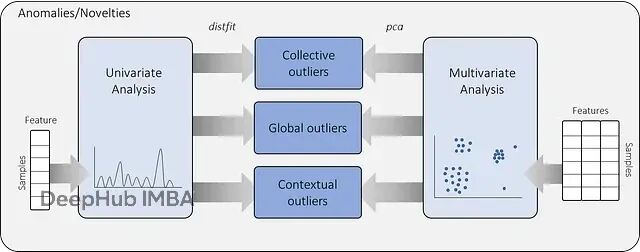
Python离群值检测实战:使用distfit库实现基于分布拟合的异常检测
本文会先讲清楚异常检测的核心概念,分析anomaly和novelty的区别,然后通过实际案例演示如何用概率密度拟合方法构建单变量数据集的无监督异常检测模型。所有代码基于distfit库实现。
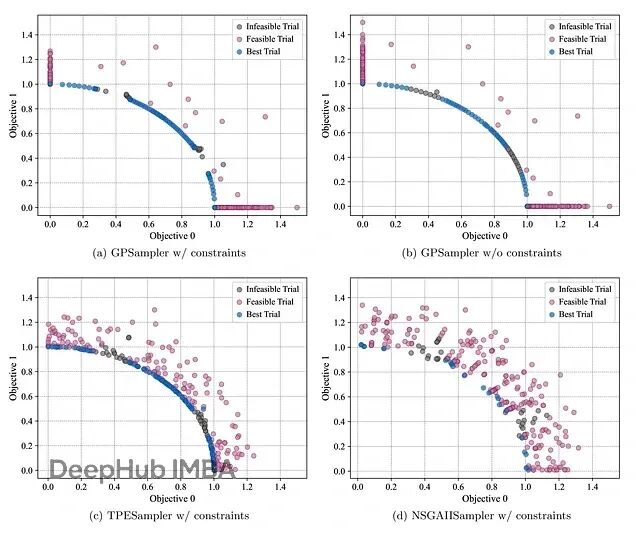
Optuna v4.5新特性深度解析:GPSampler实现约束多目标优化
Optuna在8月18日发布了最近的 v4.5版,加入了GPSampler的约束多目标优化功能,我们来看看这个新的功能。
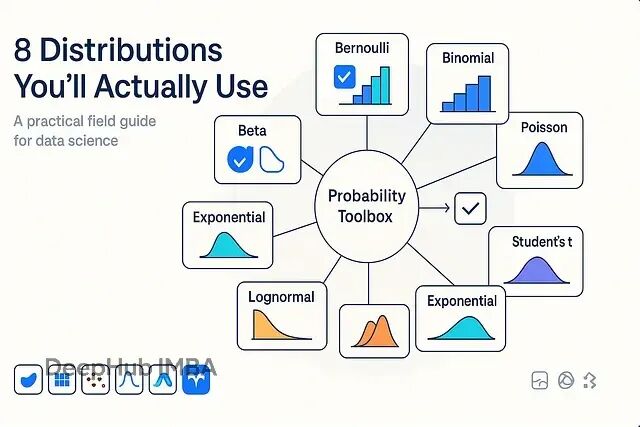
为你的数据选择合适的分布:8个实用的概率分布应用场景和选择指南
本文包含了实际会用到的概率分布速查手册,包含使用场景、代码实现和常见陷阱
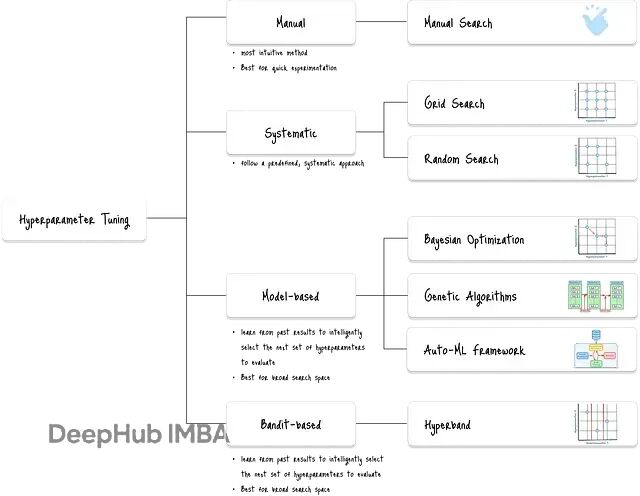
深度学习调参新思路:Hyperband早停机制提升搜索效率
Hyperband是机器学习中一个相当实用的超参数调优算法,核心思路是用逐次减半来分配计算资源。
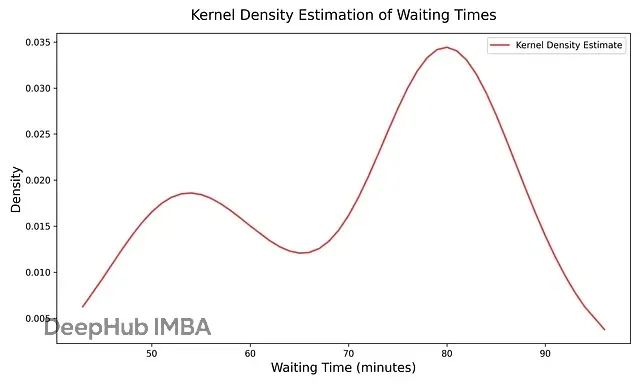
数据分布平滑化技术:核密度估计KDE解决直方图不连续问题
直方图提供了分布的粗略概念,但存在跳跃性和块状特征。核密度估计通过在数据点上放置平滑曲线并求和的方式解决了这一问题,提供了密度的连续视图。
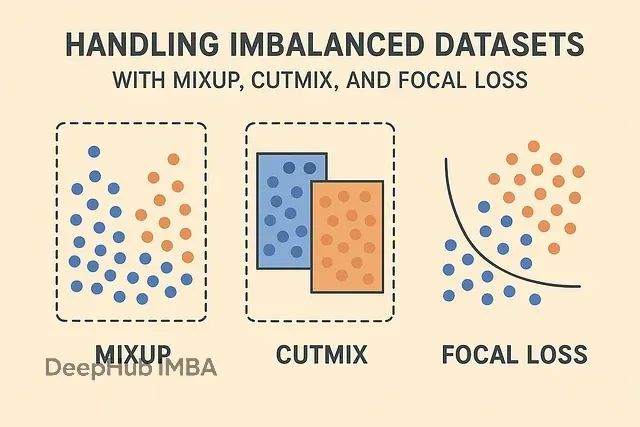
让模型不再忽视少数类:MixUp、CutMix、Focal Loss三种技术解决数据不平衡问题
针对不平衡数据集的挑战,研究界通常采用数据增强技术与损失函数优化相结合的策略。
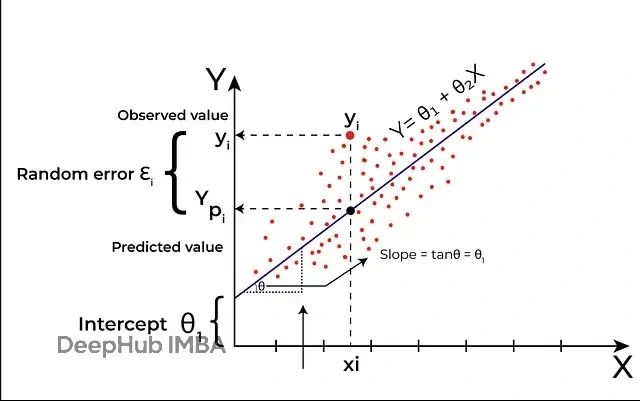
MARS算法理论和Python代码实现:用分段回归解决非线性时间序列预测问题
本文将深入探讨MARS算法的核心原理,并详细阐述其在时间序列预测任务中的应用策略与技术实现。
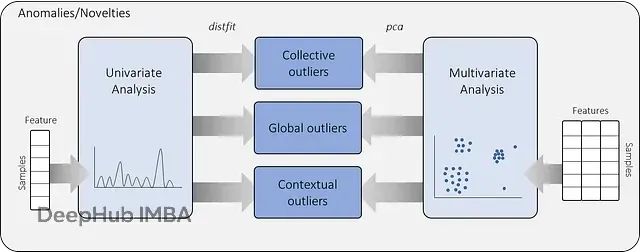
PCA多变量离群点检测:Hotelling's T2与SPE方法原理及应用指南
本文将系统阐述基于PCA的异常值检测理论框架,重点介绍霍特林T²统计量和SPE/DmodX(平方预测误差/距离建模残差)两种核心方法,并通过连续变量和分类变量的实际案例,详细演示无监督异常值检测模型的构建过程。
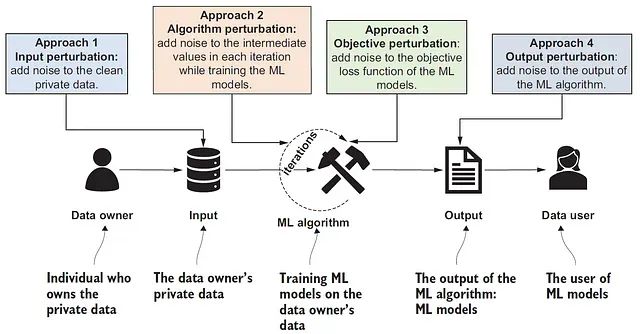
差分隐私机器学习:通过添加噪声让模型更安全,也更智能
本文探讨如何在模型训练过程中平衡实用性与形式化隐私保证这一关键问题。我们采用带有噪声梯度更新的模拟DP-SGD算法实现差分隐私机器学习。

告别低效代码:用对这10个Pandas方法让数据分析效率翻倍
本文将介绍 10 个在数据处理中至关重要的 Pandas 技术模式。这些模式能够显著减少调试时间,提升代码的可维护性,并构建更加清晰的数据处理流水线。

Python 3.14七大新特性总结:从t-string模板到GIL并发优化
本文基于当前最新的beta 2版本,深入分析了Python 3.14中的七项核心新特性。
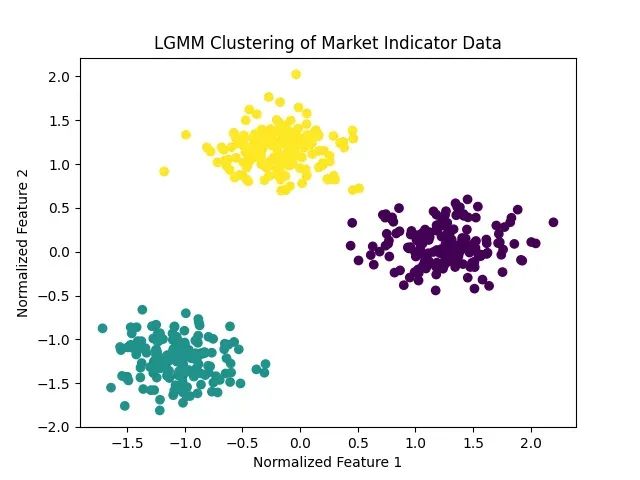
量化交易隐藏模式识别方法:用潜在高斯混合模型识别交易机会
本文将从技术实现角度阐述LGMM相对于传统方法的优势,通过图表对比分析展示其效果,并详细说明量化分析师和技术分析师如何应用此方法优化投资决策。
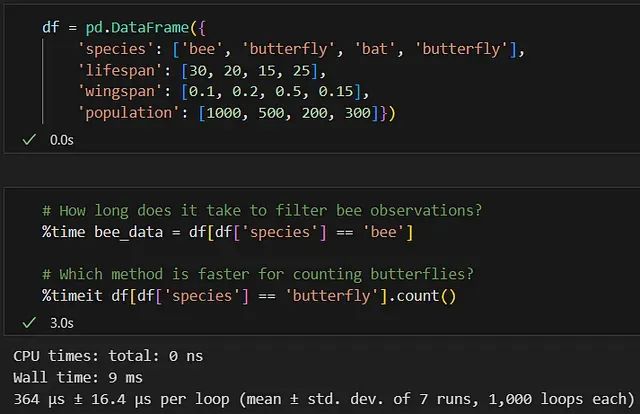
掌握这10个Jupyter魔法命令,让你的数据分析效率提升3倍
本文将详细介绍十个在实际数据科学项目中最为实用的魔法命令,并通过传粉者数据分析项目进行具体演示。
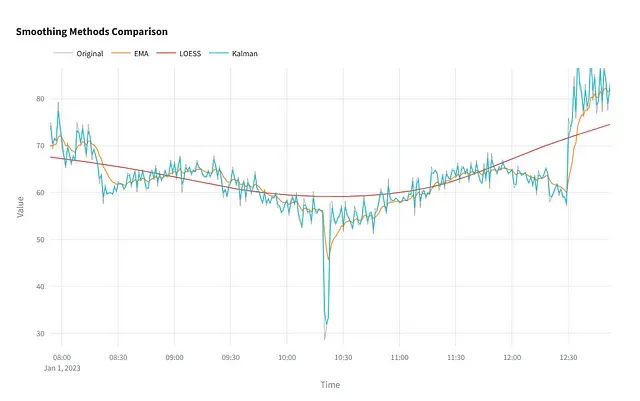
Python时间序列平滑技术完全指南:6种主流方法原理与实战应用
本文将系统介绍六种广泛应用的时间序列平滑技术,从技术原理、参数配置、性能特征以及适用场景等多个维度进行深入分析。
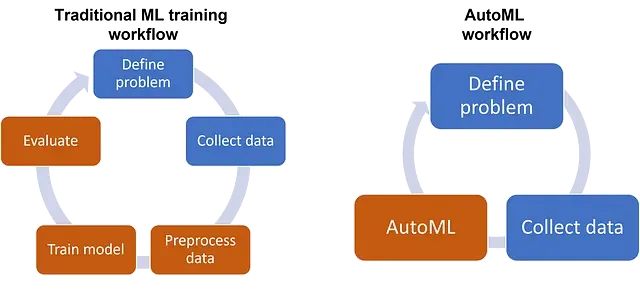
Python AutoML框架选型攻略:7个工具性能对比与应用指南
本文将系统介绍在实际项目中经过验证的主要Python AutoML库,分析各自的技术特点和适用场景。
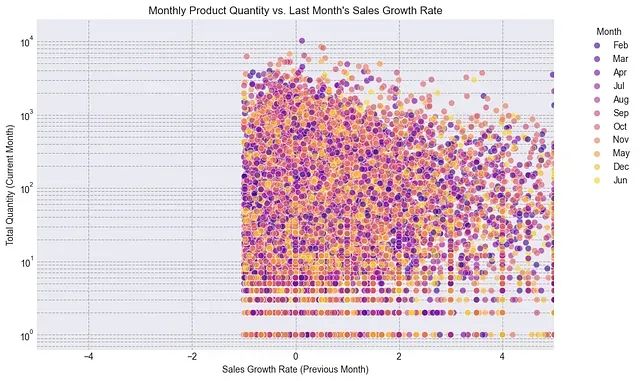
大数据集特征工程实践:将54万样本预测误差降低68%的技术路径与代码实现详解
本文通过实际案例演示特征工程在回归任务中的应用效果,重点分析包含数值型、分类型和时间序列特征的大规模表格数据集的处理方法。
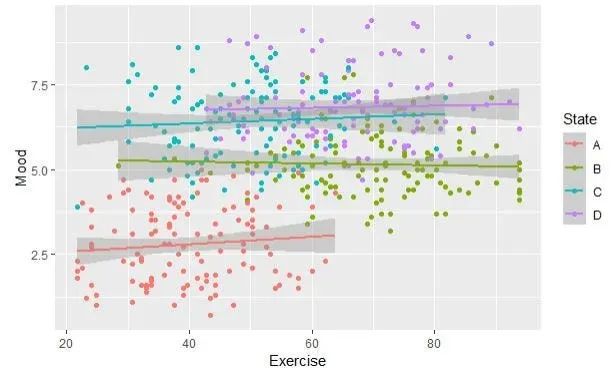
混合效应模型原理与实现:从理论到代码的完整解析
混合效应模型并非神秘的技术,而是普通回归方法在层次化结构建模方面的原理性扩展。这种理解将成为机器学习工具箱中下一个技术突破的重要基础。