Python量化投资实践：基于蒙特卡洛模拟的投资组合风险建模与分析

蒙特卡洛模拟是一种基于重复随机抽样获取数值结果的计算算法。该方法的核心原理在于利用随机性解决本质上可能具有确定性的问题。其命名源自摩纳哥的蒙特卡洛赌场，这体现了该方法中固有的随机性特征。在金融与交易等多个领域，该方法被广泛应用于不确定性场景的建模和风险影响评估。

在金融应用领域，蒙特卡洛模拟主要用于股票和加密货币市场的分析。通过构建资产价格的多种可能路径来预测未来价格走势。考虑到金融市场的随机特性，该方法特别适合于评估投资过程中的固有风险和不确定性。投资者和分析师通过该方法对不同盈利可能性进行建模，通过全面了解可能结果的分布范围及其实现概率，从而制定更为合理的投资决策。

在股票和加密货币分析中，模拟过程主要基于历史波动率和价格趋势对未来价格进行预测。具体实施步骤如下：

历史数据分析：对历史价格数据（OHLC：开盘价、最高价、最低价、收盘价）进行分析，确定平均收益率和波动率参数。
随机样本生成：基于历史平均收益率和波动率，采用统计模型生成随机日收益率序列。
价格路径模拟：将随机生成的收益率序列应用于当前价格，重复计算生成多条可能的未来价格路径。
结果分析：对模拟生成的未来价格分布进行统计分析，估计不同结果的发生概率。

本文将分两个部分详细讲解实现过程，以便更好地理解其核心原理和具体应用。

第一部分：数据获取与基础模拟

首先需要获取历史交易数据作为模拟基础。本文使用EODHD APIs提供的数据服务。EODHD提供了名为"eodhd"的Python库，可以方便地获取所需的数据。以下示例将使用标准普尔500指数的每日交易数据进行分析。

 python3-mpipinstalleodhd-U

 importnumpyasnp  
 importmatplotlib.pyplotasplt  
 fromeodhdimportAPIClient  
   
 API_KEY="<YOUR_KEY>"  
   
 api=APIClient(API_KEY)  
 df=api.get_historical_data("GSPC.INDX", "d", results=365)  
   
 print(df)

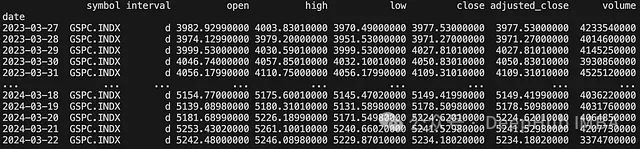
 # 计算日收益率序列
 daily_returns=df["adjusted_close"].pct_change().dropna()  
 print(daily_returns)

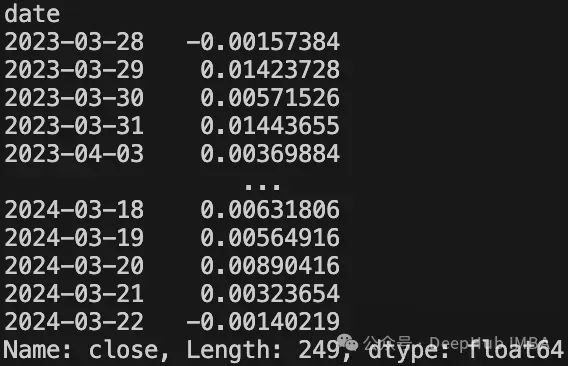
 # 定义模拟参数
 num_simulations=1000  # 模拟路径数量
 forecast_days=365    # 预测天数
   
 # 初始化模拟数组
 simulations=np.zeros((num_simulations, forecast_days))  
   
 # 生成价格路径
 last_price=df["adjusted_close"].iloc[-1]  
 foriinrange(num_simulations):  
     cumulative_returns=np.random.choice(daily_returns, size=forecast_days, replace=True).cumsum()  
     simulations[i, :] =last_price* (1+cumulative_returns)  
   
 print(simulations)

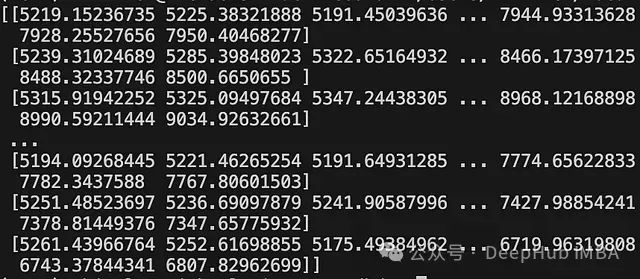
可视化模拟结果

 # 绘制价格路径
 plt.figure(figsize=(10, 6))  
 plt.plot(simulations.T, color="blue", alpha=0.025)  
 plt.title("Monte Carlo Simulation of Future Prices")  
 plt.xlabel("Day")  
 plt.ylabel("Price")  
 plt.show()

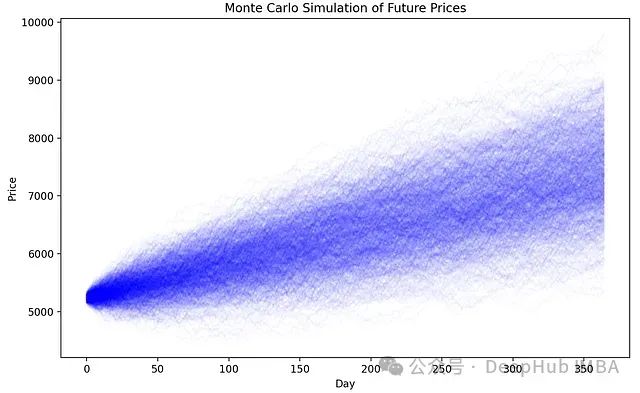
上述模拟结果展示了几个关键的技术特征：

波动率特征捕捉：模拟通过历史波动率数据捕捉了价格变动的可能范围，提供了不确定性的定量表示。然而需要注意的是，该方法基于历史波动模式的持续性假设，这在实际市场环境中可能存在偏差。
预测能力边界：虽然模拟对于理解潜在结果分布具有重要价值，但其无法准确预测具体的未来价格点位。市场条件、宏观经济因素以及突发事件都可能导致实际结果偏离模拟范围。
情景分析框架：模拟结果的分布为投资者提供了系统的情景分析框架，有助于在收益潜力与损失风险之间进行量化权衡。这种方法推动了从确定性预测向概率思维的转变。
模型依赖性：模拟精度在很大程度上取决于收益分布和波动率假设的合理性。不同的分布假设（如正态分布与对数正态分布）可能产生显著不同的结果，这凸显了模型选择和参数校准的重要性。

在理解了基础实现之后，我们将深入探讨蒙特卡洛模拟在投资风险评估和决策制定中的实际应用。通过分析第一部分生成的未来价格分布，我们可以构建量化的风险-收益评估框架。

投资决策框架的关键要素

投资目标与风险偏好量化

投资组合管理的首要步骤是明确定义投资目标并量化风险承受能力。这包括：

预期收益率的具体目标设定
风险承受能力的量化界定
投资期限的明确规划
流动性需求的评估

这些参数受到投资期限、财务目标特征以及投资者风险偏好等因素的综合影响。

模拟执行的技术实现

利用历史数据和统计模型构建预测框架，对目标投资品种（如股票、加密货币等）的价格路径进行大规模模拟。每条模拟路径代表了基于历史波动特征的一种可能市场情景。

模拟结果的量化分析

蒙特卡洛模拟输出的关键分析指标包括：

概率分布特征：通过分析模拟终值的分布特征，评估结果的离散程度。较大的离散度通常意味着更高的波动风险。
**风险价值度量(VaR)**：在给定置信水平下估计特定时间范围内的最大潜在损失。例如，95%置信水平下的VaR值表示在正常市场条件下的最大可能损失限额。
**条件风险价值(ETL)**：又称条件VaR，计算超出VaR阈值的平均损失水平，提供了尾部风险的更全面度量。

量化投资决策实例

假设进行一项10,000英镑的标准普尔500指数投资，我们需要通过蒙特卡洛模拟进行风险评估。具体目标包括：

在95%置信水平下，年度最大损失不超过2,000英镑（95% VaR约束）
实现至少10%年化收益的概率不低于50%

首先对模拟参数进行配置：

 # 设置模拟参数
 daily_returns=df["adjusted_close"].pct_change().dropna()  
   
 # 基础参数配置
 initial_investment=10000  # 初始投资金额
 num_simulations=1000     # 模拟路径数量
 forecast_days=365        # 预测期限（日）
 desired_return=0.10      # 目标收益率
   
 # 计算收益率统计特征
 average_daily_return=daily_returns.mean()  
 volatility=daily_returns.std()  
   
 print(f"Average Daily Return: {average_daily_return}")  
 print(f"Volatility: {volatility}")

需要注意的是，如果考虑对数正态收益假设，可以采用以下方法计算收益率：

 daily_returns=np.log(df["adjusted_close"] /df["adjusted_close"].shift(1)).dropna()

优化后的模拟实现代码如下：

 # 执行收益率模拟
 simulated_end_returns=np.zeros(num_simulations)  
 foriinrange(num_simulations):  
     random_returns=np.random.normal(average_daily_return, volatility, forecast_days)  
     cumulative_return=np.prod(1+random_returns)  
     simulated_end_returns[i] =initial_investment*cumulative_return  
   
 # 计算最终投资价值
 final_investment_values=simulated_end_returns  
   
 print(final_investment_values)

第二部分：风险指标的量化分析

风险价值与条件风险价值的计算实现

以下代码实现了基于模拟结果的风险价值(VaR)和条件风险价值(CVaR)的计算：

 confidence_level=0.95  
 sorted_returns=np.sort(final_investment_values)  
 index_at_var=int((1-confidence_level) *num_simulations)  
 var=initial_investment-sorted_returns[index_at_var]  
 conditional_var=initial_investment-sorted_returns[:index_at_var].mean()  
   
 print(f"Value at Risk (95% confidence): £{var:,.2f}")  
 print(f"Expected Tail Loss (Conditional VaR): £{conditional_var:,.2f}")

风险指标的技术解读

风险价值(VaR)和条件风险价值(CVaR)提供了不同维度的风险度量，它们的技术含义如下：

风险价值(VaR)分析

示例中显示的"风险价值(95%置信度)：£-1,926.81"表明：基于历史数据和当前市场条件，在95%的置信水平下，投资组合在指定持有期内的潜在最大损失不会超过1,926.81英镑。这一指标为投资者提供了在正常市场条件下的风险暴露上限。

条件风险价值(CVaR)分析

"条件风险价值：£-1,301.08"代表了VaR阈值之外（即最不利的5%情景）的平均损失水平。这一指标提供了对尾部风险更为敏感的度量，有助于评估极端市场条件下的风险暴露。

目标收益实现概率分析

 num_success=np.sum(final_investment_values>=initial_investment* (1+desired_return))  
 probability_of_success=num_success/num_simulations  
   
 print(f"Probability of achieving at least a {desired_return*100}% return: {probability_of_success*100:.2f}%")

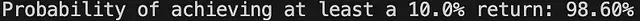
投资结果分布的可视化分析

以下代码实现了投资结果的直方图展示，并标注了关键风险和收益阈值：

 plt.figure(figsize=(10, 6))  
 plt.hist(final_investment_values, bins=50, alpha=0.75)  
 plt.axvline(  
     initial_investment* (1+desired_return),  
     color="r",  
     linestyle="dashed",  
     linewidth=2,  
 )  
 plt.axvline(initial_investment-var, color="g", linestyle="dashed", linewidth=2)  
 plt.title("Distribution of Final Investment Values")  
 plt.xlabel("Final Investment Value")  
 plt.ylabel("Frequency")  
 plt.show()

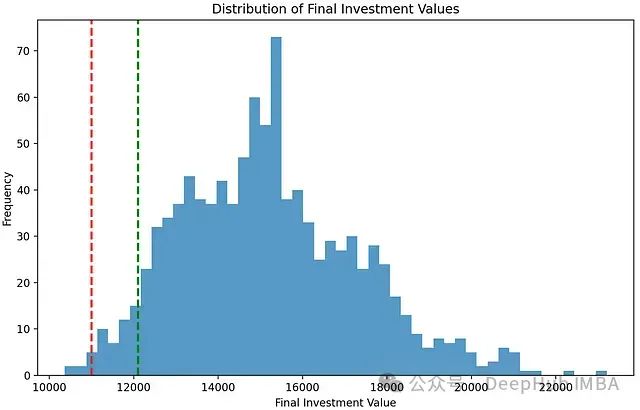
该直方图中的垂直参考线具有重要的技术含义：

收益目标线（红色虚线）

技术定义：表示达到目标收益率时的投资价值水平
计算方法：initial_investment * (1 + desired_return)
分析意义：该线右侧的分布区域代表实现预期收益目标的情景，其面积与目标实现概率直接相关

风险阈值线（绿色虚线）

技术定义：表示95%置信水平下的VaR阈值位置
计算方法：initial_investment - var
分析意义：该线左侧的分布区域代表超出预期风险容忍度的极端损失情景，其面积为5%

通过这种可视化方法，可以直观地评估：

投资结果的概率分布特征
实现目标收益的可能性
极端损失情景的发生频率和程度

完整模型实现代码

以下是整个投资风险分析模型的完整Python实现：

 importnumpyasnp  
 importmatplotlib.pyplotasplt  
 fromeodhdimportAPIClient  
 importconfigascfg  
   
 api=APIClient(cfg.API_KEY)  
 
 defget_ohlc_data():  
     df=api.get_historical_data("GSPC.INDX", "d", results=365)  
     returndf  
 
 if__name__=="__main__":  
     df=get_ohlc_data()  
   
     # 计算日收益率序列
     daily_returns=df["adjusted_close"].pct_change().dropna()  
   
     # 基础参数配置
     initial_investment=10000  # 初始投资金额
     num_simulations=1000     # 模拟路径数量
     forecast_days=365        # 预测期限（日）
     desired_return=0.10      # 目标收益率
   
     # 计算收益率统计特征
     average_daily_return=daily_returns.mean()  
     volatility=daily_returns.std()  
   
     print(f"Average Daily Return: {average_daily_return}")  
     print(f"Volatility: {volatility}")  
   
     # 执行收益率模拟
     simulated_end_returns=np.zeros(num_simulations)  
     foriinrange(num_simulations):  
         random_returns=np.random.normal(  
             average_daily_return, volatility, forecast_days  
         )  
         cumulative_return=np.prod(1+random_returns)  
         simulated_end_returns[i] =initial_investment*cumulative_return  
   
     # 计算最终投资价值
     final_investment_values=simulated_end_returns  
   
     # 风险指标计算
     confidence_level=0.95  
     sorted_returns=np.sort(final_investment_values)  
     index_at_var=int((1-confidence_level) *num_simulations)  
     var=initial_investment-sorted_returns[index_at_var]  
     conditional_var=initial_investment-sorted_returns[:index_at_var].mean()  
   
     print(f"Value at Risk (95% confidence): £{var:,.2f}")  
     print(f"Expected Tail Loss (Conditional VaR): £{conditional_var:,.2f}")  
   
     # 目标收益实现概率分析
     num_success=np.sum(  
         final_investment_values>=initial_investment* (1+desired_return)  
     )  
     probability_of_success=num_success/num_simulations  
   
     print(  
         f"Probability of achieving at least a {desired_return*100}% return: {probability_of_success*100:.2f}%"  
     )  
   
     # 结果分布可视化
     plt.figure(figsize=(10, 6))  
     plt.hist(final_investment_values, bins=50, alpha=0.75)  
     plt.axvline(  
         initial_investment* (1+desired_return),  
         color="r",  
         linestyle="dashed",  
         linewidth=2,  
     )  
     plt.axvline(initial_investment-var, color="g", linestyle="dashed", linewidth=2)  
     plt.title("Distribution of Final Investment Values")  
     plt.xlabel("Final Investment Value")  
     plt.ylabel("Frequency")  
     plt.show()

作者：Michael Whittle

标签：机器学习量化交易 Python