预测不确定性量化在数据驱动决策过程中具有关键作用。无论是评估医疗干预的风险概率还是预测金融市场的价格波动范围,我们常需要构建预测区间——即以特定置信度包含目标真值的概率区间。
**分位数回归(Quantile Regression, QR)**作为一种传统统计方法,长期以来被用于预测此类区间。与常规回归方法建模条件均值不同,QR直接对条件分位数进行建模,例如预测结果的第90百分位数。
然而单纯依赖QR在实践应用中存在显著局限性:其生成的区间在面对新数据时往往校准不足(区间过窄或过宽)。**Conformalized Quantile Regression (CQR)正是为解决这一问题而提出的创新方法,它将分位数回归与共形预测(Conformal Prediction)**技术相结合,生成既具有_自适应性_(区间宽度随输入特征动态变化,类似QR)又具有_严格统计保证_(能够达到预设的覆盖率目标)的预测区间。
本文将深入探讨CQR的理论基础、技术实现、与传统方法的比较,以及它在医疗、金融、能源和气候科学等多个领域的实际应用。
从分位数回归到共形预测
**分位数回归(QR)**是一种历史悠久的统计技术,可追溯至19世纪Galton的研究,并在1970年代得到形式化。QR方法直接估计目标变量的条件分位数,而非条件均值。例如在房地产市场分析中,QR不仅可预测给定特征下的平均房价,还能估计给定特征下房价的第90百分位值。
QR通过优化_尖点损失函数(pinball loss)_(亦称分位数损失)学习预测Y在X条件下的q分位数。QR的主要优势之一是能够自然处理**异方差性(heteroscedasticity)**问题——例如,第5百分位与第95百分位预测值之间的区间可根据数据局部噪声水平自动调整宽窄。
这种特性使QR能够生成局部自适应预测区间:在数据波动较大的区域产生更宽的区间,而在数据表现稳定的区域生成更窄的区间,从而更精确地反映预测的不确定性分布。
经典QR的关键限制在于校准问题。QR本身无法保证未来数据点有90%会落在所谓的"90%预测区间"内。理论上,QR区间的覆盖率仅在_渐近条件下_(样本趋于无穷且模型规范正确)才能达到预期水平。
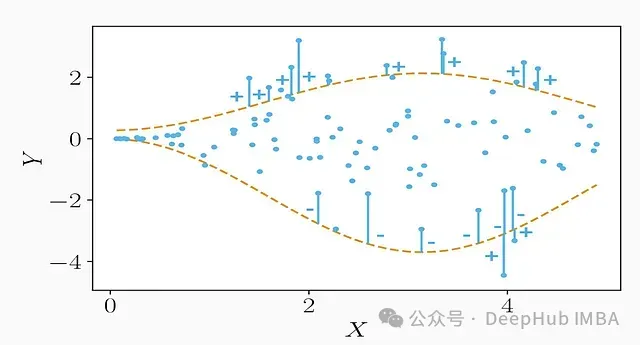
在有限样本情况下,或当模型设定不完全正确时,实际覆盖率可能与名义覆盖率存在显著偏差。图1清晰地展示了这一问题:图中展示的分位数回归模型生成的90%预测区间(阴影区域)未能完全覆盖数据样本,部分观测点落在区间之外,表明该"90%"区间在实践中的覆盖率不足。
与此相对,归纳共形预测(Inductive Conformal Prediction, ICP)作为一种现代不确定性量化方法,将校准作为其核心目标。ICP构建的预测区间具有无分布假设的有限样本覆盖保证。本质上共形方法可以应用于_任意_点预测模型(通常是均值回归模型),然后利用单独的校准数据集调整预测结果,使预测区间_通过设计_达到目标覆盖率。
ICP的唯一假设是训练数据与未来数据点满足可交换性(exchangeability)(即广义上的独立同分布条件)。对于回归问题,一种简单的_分割共形(split-conformal)_方法操作如下:首先在一部分数据上训练回归模型,然后计算校准集上的预测残差,最后确定一个阈值使得(1–α)比例的残差落在该阈值范围内。这一过程产生的预测带将以约(1-α)的概率覆盖真实值y。
ICP方法的优势在于其统计保证:当声明95%置信度时,它确实能够平均覆盖95%的新数据点。当使用均值估计器时,这种方法的限制在于生成的区间往往是均匀宽度的,或者仅轻微依赖于输入特征X(本质上是在所有预测点应用相同的残差阈值)。在异方差数据环境中,这种方法效率不高——可能导致在某些实际不需要的区域使用过度保守的宽区间,仅仅因为其他区域的数据变异性较高。
综上所述,分位数回归提供了自适应的预测区间但缺乏覆盖保证,而共形预测提供了覆盖保证但缺乏强自适应性。这自然引出了一个问题:能否将两种方法的优势结合起来?
Conformalized Quantile Regression (CQR)的工作原理
**Conformalized Quantile Regression (CQR)**正是融合上述两种方法优势的技术解决方案,它实现了"QR与CP优势的有效结合"。
由Romano、Patterson和Candès(2019)提出的CQR方法能够生成既能适应局部不确定性(如分位数回归)_又_保持严格覆盖保证(如共形预测)的预测区间。换言之,CQR"通过合并分位数回归和共形预测,产生同时适应数据底层分布特性并维持严格覆盖保证的预测区间",从而实现双重目标:_每个预测点处的区间尽可能窄,同时确保整体覆盖率的正确性_。
CQR的实现流程可以概括为以下关键步骤:
训练分位数模型:首先将数据集划分为训练集和校准集(类似于分割共形法)。使用训练集拟合两个分位数回归模型:一个预测下界分位数(如第5百分位),另一个预测上界分位数(如第95百分位),这两个模型共同界定目标预测区间。这些模型可以是任何能够预测特定分位数的回归算法,包括优化用于分位数损失的梯度提升树、随机森林或神经网络。
计算校准残差:接下来,将训练好的分位数模型应用于_校准_数据集。对于每个校准样本点(x_i, y_i),评估真实值y_i相对于分位数模型预测区间的位置关系。为每个点计算**非一致性得分(nonconformity score)**,该得分实质上度量了当y_i落在预测区间外时,其偏离预测区间的距离。
确定校正量:然后,计算校准集上所有非一致性得分的(1-alpha)分位数值。这给出了一个值qCQR,使得90%的校准残差小于或等于该值。简言之qCQR是需要添加到或从原始分位数模型区间中减去的最小额外边际量,以确保90%的校准点被覆盖。
生成最终预测区间:最后,对于任何新输入x,CQR输出区间:[q^lower(xnew)−qCQR, q^upper(xnew)+qCQR]。此区间实质上是原始QR预测区间在每侧按常数qCQR进行扩展或收缩的结果。通过构造,这种调整后的区间将覆盖约(1-α)比例的未来数据点,_即使在有限样本情况下且不依赖分布假设_。CQR利用分位数回归作为智能起点,然后通过一个统一的微调缓冲区确保覆盖保证。若分位数估计接近完美,则缓冲区qCQR将非常小(理想情况下甚至为零)。若分位数模型低估了实际分布的扩散程度,qCQR将提供必要的补偿调整。
这一方法继承了两种组成技术的核心优势:区间长度可以随输入特征x变化(因为分位数回归预测会根据特征调整),从而像QR一样捕捉异方差模式;同时,由于共形校准步骤的作用,该区间具有(1-α)的有限样本覆盖保证。从理论角度看,CQR是_分布无关的_(无需参数模型假设)并且在可交换性条件下有效——若数据点满足独立同分布假设,则可以高置信度获得≥(1-α)的覆盖率(在X和Y的联合分布上)。
下面直接比较CQR与传统分位数回归的关键差异,以突显CQR的技术优势:
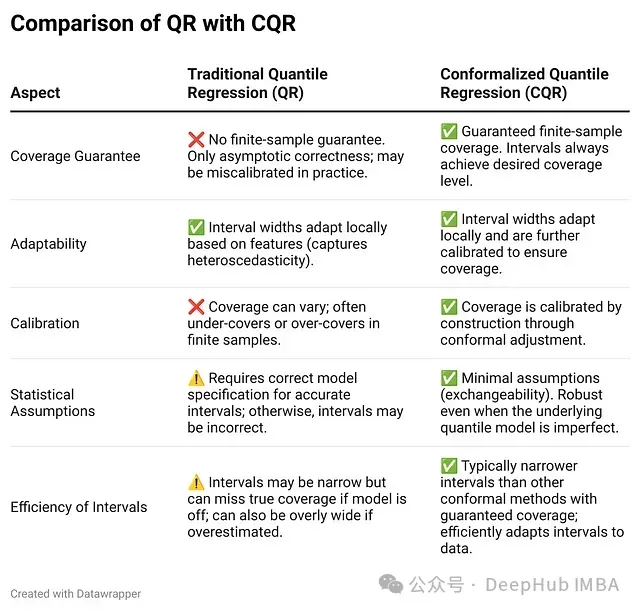
可以说CQR是分位数回归的即插即用增强版,它能够"每次都有效",默认情况下交付预期的覆盖保证。当QR模型声称某一预测为"第95百分位"时,CQR确保实际上确有约95%的结果落在该预测值之下——正如一位实践者所强调:"95%意味着真正的95%"。这种可靠性在高风险应用场景中尤为重要。
可视化比较:QR与CQR的差异
为了建立直观理解,我们回顾图1所示的场景。在该图中,分位数回归生成的预测区间未能覆盖部分数据点。若应用CQR方法,我们会使用校准集上的这些"未覆盖点"来适当扩展预测区间,直至覆盖所需比例的点。结果是所有(或几乎所有)数据点都将落入修正后的区间内,可能仅需在问题区域小幅增加区间宽度。换言之,CQR可能会在图1中的蓝色曲线上添加一个小的均匀缓冲区,略微提高上界并降低下界,直至_95%的点被包含其中_。在QR模型已经表现良好的区域,区间保持窄小,仅在必要处(如较高X值区域,QR模型原本低估了真实分布扩散)适度增宽。
实证研究证实了这一优势。例如,在一项包含29,993笔奥斯陆房屋销售数据的房价预测研究中,将CQR应用于随机森林模型后,生成的预测带宽度显著小于标准共形方法,同时仍然达到了90%的目标覆盖率。另一个医学领域的案例(从表观遗传数据预测生物年龄)发现,CQR生成的预测区间比共形均值回归方法更窄且个体间变异更大——表明CQR能更好地反映数据中的异质性,而基于均值的区间则过于保守且宽度几乎恒定。简言之,CQR通常提供两全其美的解决方案:精确、上下文敏感且可靠的预测区间。
总结
CQR(及共形预测)的应用正在迅速扩展。在机器学习研究中,CQR已被应用于时间序列预测(例如,流行的NeuralProphet库将CQR作为生成预测区间的选项)、时空数据分析(确保不同区域的预测覆盖率)以及算法公平性(一项工作引入"公平"CQR变体,确保跨不同子群体的均等覆盖率)。任何需要可靠不确定性量化的回归问题均可考虑CQR作为首选方法。其模型无关性意味着它可以包装任何前沿模型(梯度提升机、随机森林、神经网络等),使其预测具有可靠的概率特性。随着学术界和产业界对可信AI与机器学习的日益重视,CQR提供了一种相对简单却能显著提升预测模型可信度的技术增强方案。
Conformalized Quantile Regression (CQR)代表了预测建模领域的重要技术进步,它有效地结合了两个方向的优势:_灵活、数据驱动的分位数估计_与_严格的不确定性校准_。对数据科学家、分析师和研究人员而言,采用CQR能带来更为可靠的分析洞见:
CQR提供可靠的置信保证:当模型声明90%预测区间时,它确实能在实际应用中覆盖约90%的新数据结果。这种可靠性在医疗、金融等高风险决策领域尤为重要,它将预测模型转变为决策者可以真正信赖的工具。
CQR生成的自适应且信息丰富的预测区间区别于简单的不确定性带。这些区间能根据数据的局部不确定性动态调整形态。使用者能够准确识别模型不确定性较高的区域(较宽的区间表明该区域波动性更大或数据覆盖不足)与模型确定性较高的区域(较窄的区间)。这提供了更深入的分析视角,例如识别"模型对中等范围的案例预测较为确定,但对极端案例预测不确定"的模式——这类信息本身可以指导进一步行动,如针对极端案例收集更多数据。
CQR具有对分布异常的稳健性:由于其共形特性,即使数据具有异常误差分布、重尾特征或模型规范略有不准确,CQR方法也不会失效。该方法基于最少的假设,利用数据本身进行校准。这种稳健性使CQR能够跨多种应用场景部署,无需为每种情况专门调整——这是实际应用中的重要优势。
CQR提供实用的可获取性:实现CQR不再仅是理论练习——它已通过如MAPIE(面向scikit-learn用户)等库实现,并已集成到多个领域特定工具中。这降低了采用门槛。如果能训练回归模型,则只需几行额外代码即可应用CQR并获得更为丰富的预测输出。
如果你一直依赖传统分位数回归构建预测区间,现在或许是时候考虑"告别传统分位数回归,拥抱CQR"。通过对分位数预测进行共形化处理,您能确保模型不仅针对正确的分位数,还能以统计保证的方式达成预定目标。这将带来更精确、更可靠的预测洞见,支持在不确定环境中做出更明智的决策。
作者:Valeriy Manokhin