大过节的qwen发布了image 2512,DeepSeek这边就偷摸的在arXiv 上挂出了这篇 mHC: Manifold-Constrained Hyper-Connections (arXiv:2512.24880),哪个正经公司在最后一天还发论文啊。
简单的看了一下,说说我的看法: 这回DeepSeek又要对 残差连接(Residual Connection)出手了。
现在我们模型的底层架构就是叠 Transformer Block,而过去这十年,对于每一层的堆叠,恺明大神的 ResNet 也就是那个 y=x+f(x),几乎行业的“公理”。它通过 Identity Mapping(恒等映射),可以让信号能无损传下去,梯度也能无损传上来,这就保证了咱们能把模型堆到几百上千层还不崩。
但 DeepSeek 团队之前(大概是去年 9 月那会儿)提了个 Hyper-Connections (好像看的人不多,我当时没太注意这个) 的概念,觉得简单的相加太浪费了就搞了个更复杂的连接方式来扩宽层间的信息通路。但是一旦你动了那个“相加”,Identity 的属性就没了,梯度传播就开始不稳定,这样训练起来特别容易炸他们管这叫 Seesaw Effect(跷跷板效应)。
这篇 mHC 就是来填这个坑的,咱们顺着逻辑拆解一下。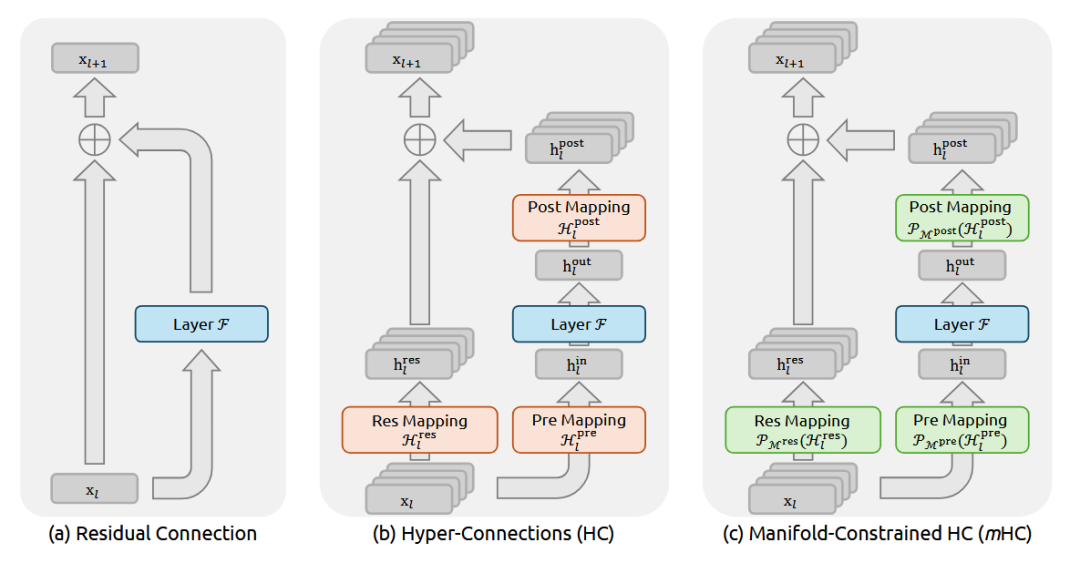
这就引出了 mHC 的核心:流形约束(Manifold Constraint)。
别被这数学名词吓着:之前的 HC 是想让连接权重随便长,结果就长歪了;现在的 mHC 就是给这些权重矩阵加了个限制。DeepSeek 在数学上证明了,如果把这些超连接的权重矩阵强制投影到一个特定的流形空间里就能在保留 HC 那种高带宽、多通路优势的同时,还把 Identity Mapping 的属性给找补回来。
也就是说他们在数学层面上造了一个“既要有又要”的结构:既要连接方式足够复杂多变,能捕捉更高级的特征交互;又要信号传播像 ResNet 一样顺滑,不至于在深层网络里迷路。
这里的“流形”具体由两个关键的数学性质构成:
第一是 谱范数约束(Spectral Norm Constraint),他们强制要求连接矩阵的谱范数 ∥W∥2≤1。这在动力系统里叫“非扩张”(Non-expansive)。只有当矩阵的最大奇异值被摁在 1 附近,信号能量在深层传播时才不会发散。
第二是 双重随机矩阵(Doubly Stochastic Matrices), 这是一类行和、列和都为 1 的非负矩阵。这玩意儿有个极好的代数性质叫 闭包性(Compositional Closure)。两个双重随机矩阵乘起来它还是双重随机的,所以这就保证了无论网络堆多深,整体的变换性质不变。更重要的是,这让每一层的输出变成了上一层的 凸组合(Convex Combination),从根本上恢复了训练的稳定性。
并且论文里面包含了很强的理论推导,对于信号传播(Signal Propagation)的分析非常扎实,直接指出了为什么之前的架构在超深层会遇到瓶颈,而 mHC 是怎么通过约束奇异值分布来解决这个问题的。(ps:DeepSeek 的日子也是好起来了,做实验都敢用27B的模型了,HC那篇用的可以是7B的)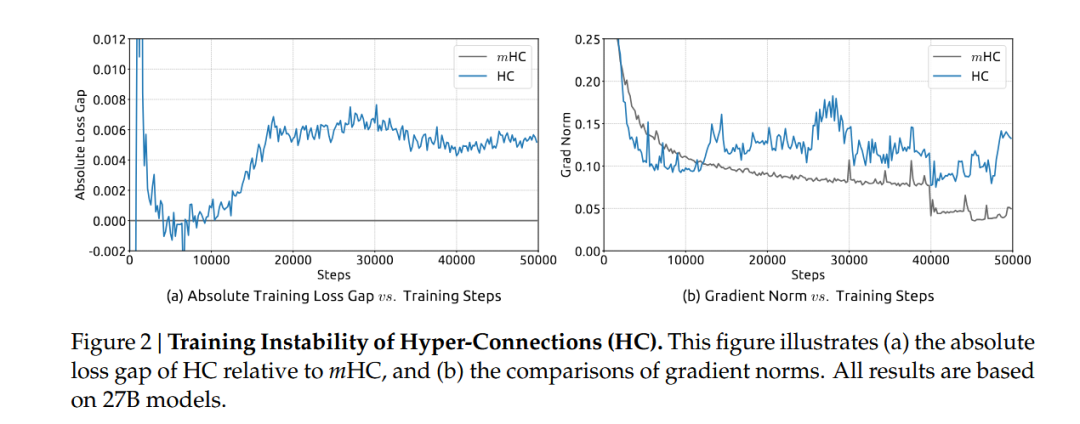
论文里还有一段非常精彩的理论分析,是从 动态系统(Dynamical Systems) 的角度去看的。
如果你把层数看作时间步,深层网络其实就是一个离散的动态系统。而且这篇论文证明了在流形约束下,这个系统的 Lyapunov 指数是受控的。他们通过一种类似 Projecting(投影)的手法,确保权重矩阵始终保持良好的 谱性质(Spectral Properties)。说的通俗点就是:不管怎么更新,这些矩阵在数学性质上必须看起来像一个“稍微扭曲了一点点的 Identity Matrix”,而不是一个完全随机的矩阵。
这就从理论上解释了为什么 mHC 可以堆叠到成百上千层而不崩塌,这部分其实是对现有架构理论的一个重要补充。以前我们只知道“加个残差就好使”,现在 mHC 告诉我们:“只要你在流形上走路,哪怕姿势复杂点,也不会摔倒”。
而且熟悉 DeepSeek 风格的朋友都知道,他们从来不只聊数学,还必须要聊 System Efficiency。
mHC 这个架构显然是做过严格的 Infrastructure Optimization 的。如果只是理论上好使但拖慢了训练速度,DeepSeek 是绝对不会用的。他们在论文里也提到了这点,这种特殊的连接方式配合专门优化的 CUDA kernel,可以把额外的计算开销压缩到了几乎可以忽略不计的程度。
这就很可怕了,等于是在算力成本几乎不变的情况下,白嫖了模型表达能力的上限。在实际的大规模训练吞吐上并没有造成明显的 overhead。
这对咱们行业意味着什么?
我觉得这可能是“后 Transformer 时代”的一个重要信号。以前咱们扩模型,就是简单粗暴地增加层数、增加宽度,属于“堆料”。但 mHC 提示了一个新的方向:层与层之间的拓扑结构(Topology)本身,还有巨大的挖掘空间。
如果这种基于流形约束的连接方式被验证能 scaling up 到万亿参数级别(论文说 671B 的 MoE 模型是ok的),那咱们以后设计大模型,可能就不再是简单的搭积木而是要开始研究积木之间的粘合剂怎么调配了。
mHC 的出现不仅修复了 Hyper-Connections 的缺陷,更重要的是它将深度学习架构设计的视角从单纯的“连接图”提升到了“参数流形”的高度。随着基础模型对效率和能力的要求日益严苛,mHC 所代表的几何约束设计理念,极有可能成为未来几年 AI 基础设施的核心标准之一。
论文: