你有没有过这样的经历?使用一款减肥app,通过它的图表来监控自己的体重变化,并预测何时能达到理想体重。这款app预测我需要八年时间才能恢复到大学时的体重,这种不切实际的预测是因为应用使用了简单的线性模型来进行体重预测。这个模型将我所有过去的体重数据进行平均处理,然后绘制一条直线预测未来的体重变化。然而,体重减轻通常不会呈线性发展,使用更复杂的数学模型,如泊松回归,可能会更加贴近真实情况。
在探讨体重减轻的模型时,我们通常会遇到各种统计分布,其中最常见的是正态分布和泊松分布。正态分布,因其钟形的概率密度函数而广为人知,常用于描述自然现象中的随机变量,比如人的体重。它假设数据围绕一个中心值(平均值)对称分布,并且数据的分散程度(标准差)决定了分布的宽窄。
在处理计数数据,如一定时间内的体重变化次数时,泊松分布则显得更为合适。泊松分布用于描述在固定时间或空间内发生的独立事件的数量,适用于预测罕见事件。这在体重管理应用中尤为重要,因为体重的减少往往是非连续和间歇性的,可能受多种因素影响,如饮食、运动习惯等。
统计分布何来?
统计分布是统计推断领域的重要工具,它为数据分析和预测提供了基础。对非统计专业的学生,我通常用“数字平均下来是如何分布的”来定义分布。例如,正态分布中,大多数样本的平均值会相同。有些平均值会与“平均的平均值”相差极远,它们出现在分布的尾部。但大多数平均值会集中在中间,给分布一个钟形的形状。
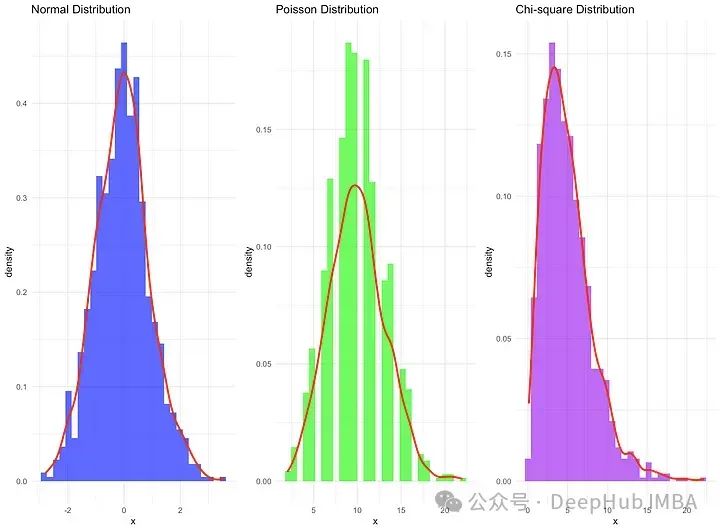
根据数据的性质和所需的分析类型,会使用不同的分布。但是并不是所有的数据都符合正态分布。本文我们研究三种常见分布以及我们如何使用它们:正态分布、泊松分布和卡方分布。
正态分布
正态分布,也称为高斯分布,是统计学中使用最广泛的概率分布之一。这种分布以高斯的名字命名,最早在18世纪被描述。正态分布以其钟形曲线为特征,由两个参数定义:均值(平均值)和标准差。
正态分布用于数据倾向于围绕一个中心值聚集,且没有左右偏差的情况。它在心理学、金融和自然科学等多个领域都有应用。例如,一个大型人群中的智商分数、身高和血压测量值通常遵循正态分布。
你可能已经看到很多人使用它,比如听说过“按曲线打分”,这是学生们在课程中担心成绩时使用的术语。
假设你想描述你所在城市的胆固醇分布。你的城市有450,000名居民,但你只能测试1,000人。你抽取了1,000名居民的样本,并进行了血液测试。平均(均值)胆固醇为145毫克/分升,标准差为35毫克/分升。
你的样本看起来是这样的,胆固醇水平在X轴(水平方向),具有该水平的人数在Y轴(垂直方向)。
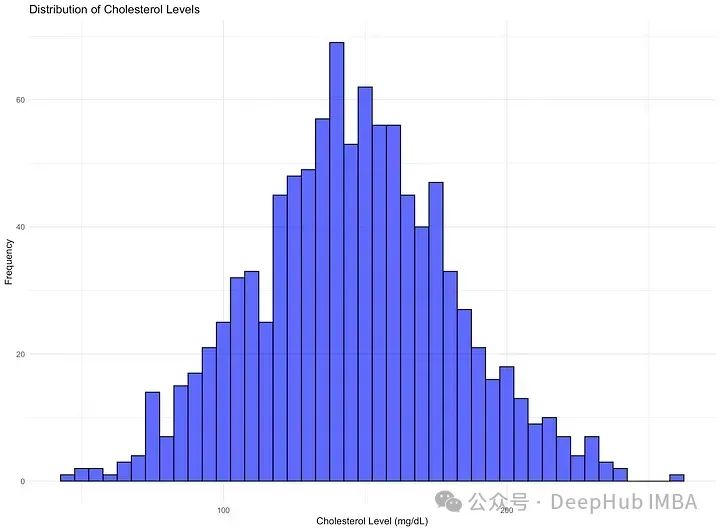
根据正态分布假设,你可以推断出城市中大约有26,118人(约5.8%)的胆固醇超过200毫克/分升。而超过200毫克/分升被认为是异常的,这样就可以为你的城市中需要治疗高胆固醇的人数做准备。
这个结果来自于一个样本中的1,000人,而无需对全城进行测试。正态分布可以用于模拟人群中某些疾病的传播。但你需要确保人群中的数据遵循正态分布。
形态:正态分布是一种连续分布,其图形呈现为著名的钟形曲线,对称且单峰,中心位于平均值(均值)。
参数:由两个参数决定——均值(μ)和标准差(σ),均值决定分布的中心位置,标准差决定分布的宽度即数据的波动范围。
应用:正态分布在自然和社会科学中极为常见,用于描述误差、衡量分数、身高、血压等自然现象和人类特征。
泊松分布
泊松分布是以法国数学家泊松的名字命名,于1837年引入。这种分布描述了在固定的时间或空间间隔内,给定数量的事件发生的概率,前提是这些事件以已知的恒定平均率独立发生。
这里我们讨论的是事件的计数,而不是像胆固醇水平那样从0到无穷大的数据测量。我们使用泊松分布来预测诸如城市中的预期谋杀案数量,或某一天急诊部的访问次数等。但是计数的独立性很重要,因为并不是所有事件都是独立的。
所以我们以一个城市的心脏病发作,并假设它们彼此独立为例。也就是说,我们不会有诸如天气或呼吸道疾病这样的混杂变量贯穿一座城市,所以不会将一个心脏病发作的概率与下一个心脏病发作的概率联系起来。
再次以450,000人为例,想模拟下个月的心脏病发作数量,我们这样做的目的是为紧急医疗服务和医院的人员、药品及医疗设备的可用性做好准备。所以使用过去30年的数据(360个月),计算出平均每月有10起心脏病发作。(再次强调,这是理论上的,只是假设,没有任何意义)
你的数据在图形上看起来是这样的:
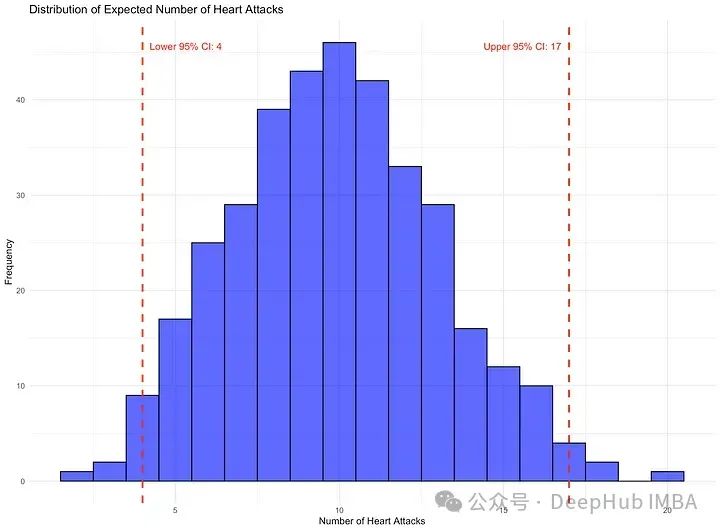
根据这30年的数据,有95%的把握认为下个月将看到4到17起心脏病发作。如果低于或高于这个范围,就可能会有什么外在的因素施加了影响,比如大量人群开始使用一种新的抗心脏病药物,或一大群有高风险因素的人同时生病。(95%是按惯例,也可以根据分析找到任何认为合适的置信水平。)
如果使用正态分布进行这个分析,下个月的心脏病发作数量将在4.5到16.4之间。这与泊松分析的结果接近,这是因为中心极限定理。但是使用泊松分布对于罕见事件的计数数据总是更好。正态分布只有在你的数据是连续的(计数不是)、符合正态分布、独立且不罕见的情况下才有帮助;或者如果你想近似泊松分布的结果时才使用。
形态:泊松分布是一种离散分布,用于描述在固定时间或空间内发生的独立事件的次数。
参数:由一个参数 λ(事件发生的平均率)决定,λ越大,分布越平滑接近对称形态。
应用:泊松分布通常用于计数数据,如某时间段内发生的交通事故数、电话来电次数、某地区一定时间内的犯罪次数等。
卡方分布
卡尔·皮尔逊在1900年首次引入卡方分布。卡方分布通常用于独立性测试和拟合优度测试。它有助于确定分类变量之间是否存在显著的关联,或者样本是否符合预期的分布。
分类变量没有合理的顺序,如眼睛颜色。它可以是棕色、蓝色、绿色或其他。不是说蓝色必须在绿色之前,或棕色在蓝色之前。它们没有顺序。
在公共卫生研究中,卡方检验可用于检查吸烟状态(吸烟者与非吸烟者)与肺癌发病率之间的关系。通过应用卡方分布,研究人员可以确定这两个分类变量之间是否存在显著的关联。
假设有450名60岁的吸烟者和450名60岁的非吸烟者。查看他们的病历,在吸烟者中450人中有202人曾被诊断出肺癌。在非吸烟者中450人中有22人被诊断出肺癌。
仅仅用“肉眼”就可以看出那些吸烟的人患肺癌的风险更高: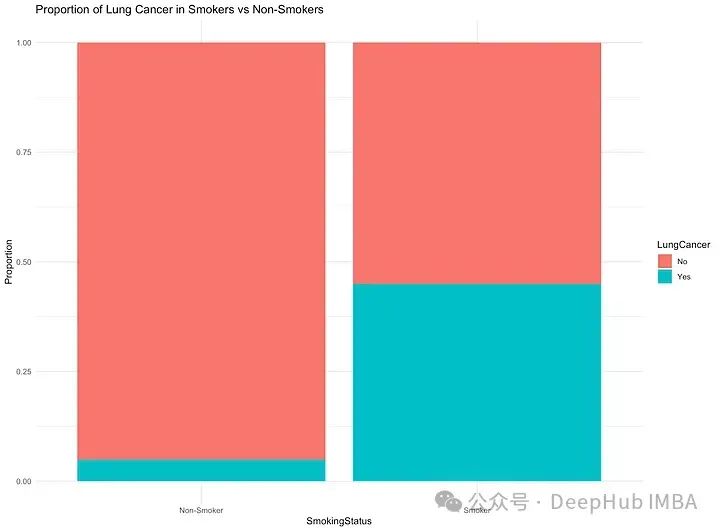
但如果实际上吸烟者和非吸烟者之间的肺癌发病率没有差异,看到这些结果的概率是多少?你的结果有多大可能是错误的?这是p值。
这个数字非常小:0.00000000000000022
我们无法使用线性回归,因为这是分类数据。所以就需要进行逻辑回归,将吸烟和非吸烟编码为0和1;然后类似地对癌症和无癌症进行编码。计算给定吸烟状态的癌症几率。然后将这些几率转换为自然对数,将0和1的类别转换为更连续的分布。就可以预测给定吸烟状态的癌症对数几率,包括95%的置信区间等等。
对于简单地比较两个分类变量各有两个类别的情况(流行病学中的经典2x2表),上述的卡方独立性测试已经足够好。但是当你必须考虑其他因素,如社会经济状态、年龄或种族/性别时,使用逻辑回归更好。
形态:卡方分布是一种连续分布,形态不对称,其形状随自由度的增加而逐渐接近正态分布。
参数:由自由度(df)决定,自由度通常与样本大小或检验中涉及的类别数相关。
应用:卡方分布主要用于分类数据的假设检验,如检验两个分类变量之间是否独立(卡方独立性检验)或一个观测频数分布是否符合期望频数分布(拟合优度测试)。
线性回归时为什么要假设数据是正态分布的
在线性回归分析中,假设数据符合正态分布主要是为了便于进行统计推断,特别是关于回归参数(如斜率和截距)的假设检验和置信区间的计算。这种假设主要关注模型残差(误差项)的分布。以下是这一假设的几个关键原因和其统计意义:
1、中心极限定理
中心极限定理指出,大量独立同分布的随机变量之和趋于正态分布,不论原始变量的分布如何。在线性回归中,如果样本量足够大,即使残差不是完美的正态分布,估计的参数的分布也会接近正态分布。这使得正态分布的假设在实际应用中更具弹性。
2、统计推断的简便性
正态分布假设简化了许多统计推断任务。例如,如果残差是正态分布的,那么回归系数的抽样分布也将是正态的。这使得使用标准的t检验和F检验来评估模型参数的显著性成为可能,因为这些测试依赖于正态性假设来推导其概率分布。
3、最小化估计误差
正态分布假设支持最小二乘法(OLS)估计的有效性。当残差正态分布时,OLS估计器是“最佳”的线性无偏估计器(BLUE),这意味着在所有线性无偏估计中,它具有最小的方差。
4、处理异常值
正态分布的假设有助于识别异常值。在正态分布的假设下,大多数数据点应聚集在均值周围,只有少数数据点会落在分布的尾部。如果观察到的残差远离预期的正态分布,这可能表明模型中存在异常值或模型设定错误。
5、置信区间和预测
正态分布的假设允许构建围绕回归线的置信区间和预测区间。这些区间为基于模型的预测提供了可靠性度量,使得我们可以估计模型预测的不确定性。
尽管正态分布的假设为线性回归提供了许多统计上的便利,但在实际应用中,数据可能不总是遵循这一假设。因此,进行适当的诊断检查是重要的,例如检查残差图来评估正态性、独立性和方差齐性(同方差性)。如果发现违背这些假设的证据,可能需要使用更复杂的统计模型或变换数据来适应更适合数据的模型,比如泊松回归。
总结
我们介绍了3个常见的分布,下面是它们的一些核心区别:
- 数据类型:正态分布用于连续数据,泊松分布用于计数数据,卡方分布用于分类数据的分析。
- 分布形态:正态分布是对称的,泊松分布和卡方分布通常是不对称的。泊松分布的偏斜度依赖于参数 λ,卡方分布的偏斜度依赖于自由度。
- 应用场景:正态分布用于模型连续变量的自然现象,泊松分布适用于事件的计数模型,卡方分布适用于进行分类数据的统计检验。
应用场景:
正态分布是统计学中最为人熟知的分布之一,通常用于描述自然和社会科学中的现象,如人类的身高、血压、考试成绩,以及工程产品的尺寸等。它的特点是数据在均值周围对称分布,形成著名的钟形曲线。由于中心极限定理,即使原始数据不符合正态分布,大量独立随机变量的平均值也会趋近于正态分布,这使得正态分布在金融模型中也广泛应用于描述例如股票回报率等。
泊松分布用于描述特定时间或空间内发生的离散事件次数,如电话呼入次数、网站点击量或某病种的发病率。这种分布适用于事件独立随机发生,且平均发生率相对稳定的情况。例如,在交通领域,泊松分布可以用来预测一定时间内通过某一点的车辆数。
卡方分布则主要用于分类数据的统计测试,如拟合优度测试和独立性测试。这使得卡方分布在社会科学研究中尤为重要,用于分析不同人群间的行为或特征的差异。例如,卡方分布可以用来检验吸烟与肺癌之间的关联性,或者分析不同广告对不同性别观众的影响是否存在显著差异。