“偏差-方差权衡”是ML/AI中被经常提到的一个流行概念。我们这里用一个直观的公式来对它进行解释:
MSE = Bias² + Variance
本文的目的并不是要证明这个公式,而是将他作为一个入口,让你了解统计学家如何以及为什么这样构建公式,以及我们如何判断是什么使某些估算器比其他估算器更好。

用公式来概括细节虽然很直观但是并不详细,所以本文将详细解释为什么我说这个公式是正确的。
先决条件
如果你对一些核心概念有一定的了解,这些东西就会更容易理解,所以这里有一个快速的关键词列表:
偏差;分布;估计;估计量;期望值E(X);损失函数;均值;模型;观察;参数;概率;随机变量;样本;统计;方差V (X)
这些基本的统计学概念你都应该有一个基本的概念,如果有一些疑问请自行搜索。
E(X)和V(X)
期望值 E(X)
期望值,写为 E(X) 或 E(X = x),是随机变量 X 的理论概率加权平均值。
可以通过对X可以取的每个潜在值x乘以相应的概率P(X= x)进行加权(相乘),然后将它们组合起来(如对身高等连续变量用∫表示,或对离散变量求和,如身高取整到最接近英寸:E(x) =∑x P(X= x)

如果我有一个公平的六面骰子,X可以取{1,2,3,4,5,6}中的每一个值,其概率为1/6,所以:
E (X) = (1) + (1/6) (2) (1/6) + (3) (1/6) + (4) (1/6) + (5) (1/6) + (6) (1/6) = 3.5
或者说 3.5是X的概率加权平均值,并且没有人在乎3.5是不可能在骰子结果中出现的。
方差V (X)
上面E(X)公式中的(X - E(X))²替换X得到分布的方差:
V(X) = E[(X - E(X))²] = ∑[x - E(X)]² P(X = x)
这是一个定义,所以这部分没有证明。让我们计算骰子的方差:
V(X) = ∑[x - E(X)]² P(X=x) = ∑(x - 3.5)² P(X=x) = (1–3.5)² (1/6) + (2–3.5)² (1/6) + (3–3.5)² (1/6) + (4–3.5)² (1/6) + (5–3.5)² (1/6) + (6–3.5)² (1/6) = 2.916666…
如果你处理的是连续的数据,你会使用积分而不是求和,但这是思想是一致的。
V(X)公式的另外一个备选
下面的证明中,我们将对方差公式进行一些转换,用最右边的位替换中间位:
V(X) = E[(X - E(X))²] = E[(X )²] - [E(X)]²
下面是这个公式是如何推导出来的:
V(X) = E[(X - E(X))²]
= E[X² - 2 X E(X) + E(X)²]
= E(X²) - 2 E(X) E(X) + [E(X)]²
= E[(X )²] - [E(X)]²
这是如何发生的以及为什么会发生的关键位置是从第2行到第3行。用括号这样做的原因是期望值是和/积分,所以无论我们对常数总和/积分用括号做什么,也可以对期望值做什么。这就是为什么如果a和b是常数,那么E[aX + b] = aE(X) + b。另外E(X)本身也是常数经过计算后它不是随机的,所以E(E(X)) = E(X)这样就简单的进行了化简。
关于符号的注释
Estimand(你想要估计的东西,估计目标或者叫被估计值)通常用朴素的希腊字母表示,最常见的是 θ。(“th”应该有自己的字母,这就是我们在英语中使用的字母“theta”;“th”足够接近“pffft”,使 θ 成为统计学中标准占位符的真正绝佳选择 .)
估计θ是参数,所以它们是(未知的)常数:E(θ) = θ和V(θ) = 0。
估算量(你用来估算估算值的公式)通常是在希腊字母上加上一些特殊的标记,比如在θ上加上一个小帽子,就像这样:
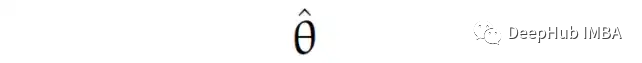
注:一般应为都会念成 xx hat,例如吴恩达老师的机器学习和深度学习课程中就是这样,有兴趣的可以再去看看
推导MSE公式
估计器(Estimators )是随机变量,他会跟我们的数据进行变换得到一个估计(“最佳猜测”)。估计(Estimate)是一个常数,所以可以把它当作一个普通的数字。为了避免混淆,我们提前先说下。
Estimand:θ,我们要估计的东西,一个常数。
Estimator,我们用来获得估计值的公式,它是一个取决于你获得的数据的随机变量。
Estimate :θ_hat,一旦我们将数据送入估计器,最后就会出现一些数字,这就是估计。
现在为了知道我们的估计器是否有效,我们要检查他的估计值 θhat ,期望它接近估计目标 θ。所以随机变量 X = (θhat - θ) 的 E() 是我们先要介绍的:
E(X) = E((θhat - θ)) = E(θhat ) - E(θ) = E(θhat) - E(θ) = E(θhat) - θ
这个量在统计学中有一个特殊的名称:偏差(bias)。
无偏估计器是E(θhat) = θ的估计器,这意味着我们可以期待我们的估计器是正确的(平均)。因为偏差指的是“系统地偏离目标的结果”。或者更恰当地说,偏差是我们的估计(θhat)给出的结果和我们的估计目标(θ)之间的期望距离:
Bias = E(θhat) - θ
选择“最佳”估计器
如果你喜欢无偏估计器,那么你可能会知道 UMVUE。这是uniformly minimum-variance unbiased estimator的首字母缩写词,它指的是在无偏估计器中进行最佳选择的标准:如果它们都是无偏的,则选择方差最小的那个!
更通俗的说法就是就是“如果有两个具有相同偏差的估计器,我们选择方差较小的一个”
还有许多不同的方法可以选择“最佳”估算器。因为“好”的属性包括无偏性、相对效率、一致性、渐近无偏性和渐近效率等等。前两个是小样本属性,后三个是大样本属性,因为它们处理的是随着样本量的增加时估计器的行为。如果随着样本量的增加最终达到目标,则估计量应该与被估计量是一致的。
这里效率也是一个值得关注的的属性,不仅时间是金钱,投入也是金钱。由于效率与方差有关,让我们尝试将 X = (θhat - θ) 代入方差公式:
方差 V(X) = E[(X)²] - [E(X)]²
变为 V(θhat -θ) = E[(θhat - θ)²] - [E(θhat - θ)]²
方差衡量的是一个随机变量的扩散,所以减去一个常数(你可以把参数θ当作一个常数)它只是平移了所有的东西,而不改变扩散,V(θhat - θ) = V(θhat),所以:
V(θhat) = E[(θhat - θ)²] - [E(θhat) - E(θ)]²
现在我们重新排列这些项,并常数E(θ) = θ
E[(θhat - θ)²] = [E(θhat) - θ]² + V(θhat)
现在再来看看这个公式,因为它有一些特殊的东西和特殊的名字。还记得偏差吗?
Bias = E(θhat) — θ
能在公式中找到它吗?当然可以!
E[(θhat - θ)²] = [Bias]² + V(θhat) = Bias² + Variance
左边的东西到底是什么东西呢?这是一个有用的数量,但我们在命名它时并不是很有创意。由于“误差”是描述射击着陆点 (θhat) 和瞄准点 (θ) 之间差异(通常记为 ε)的一种恰当方式,因此 E[(θhat - θ)²] = E(ε²)。
E(ε²)又被称作为均方误差!简称 MSE。它的字面意思是 E(ε²):我们取均方误差 ε² 的平均值(期望值的另一个词)。MSE 是模型损失函数最流行的(也是普通的)选择,而且它往往是我们学习的第一个损失,所以我们就得到了:
MSE = Bias² + Variance
总结
我们已经完成了数学计算,希望这篇文章可以从另外一个角度说明机器学习中的偏差-方差权衡是关于什么的。这样我们在学习时也可以开阔更多的思路。
作者:Cassie Kozyrkov