在实际应用中,我们经常需要从给定的概率密度函数(PDF)中抽取随机样本。这种需求在多个领域都很常见,例如:
- 估计统计量
- 进行蒙特卡洛模拟
- 生成粒子系统用于物理仿真
对于标准概率分布,如均匀分布或高斯分布(正态分布),
numpy
和
scipy
生态系统提供了现成的解决方案。通过
numpy.random
或
scipy.stats
模块,我们可以方便地生成这些分布的随机样本。
然而,现实世界中的概率分布往往远比标准分布复杂。例如,考虑以下非高斯分布:

图1:非高斯概率密度函数示例。等高线表示等密度线,在对数空间中等间隔分布。
对于这类复杂分布,如何有效地生成随机样本呢?
传统上,有几种广泛使用的方法可以从任意分布中抽样,如拒绝采样法和马尔可夫链蒙特卡洛方法(MCMC)。这些方法都是可靠的技术,并且有一些优秀的Python实现。例如,emcee是一个在科学计算中广泛使用的MCMC采样器。
然而,这些传统方法通常需要复杂的设置和参数调整:
拒绝采样法需要选择合适的提议分布,不当的选择可能导致采样效率极低。
MCMC方法需要关注样本的收敛性,通常需要进行后验分析来评估。
lintsampler
是一个纯Python实现的库,能够高效地从任意概率分布中生成随机样本。本问的作者就是
lintsampler
的开发者之一。
lintsampler
的设计目标就是解决这些问题,提供一种简单高效的采样方法。使用
lintsampler
的基本流程如下:
fromlintsamplerimportLintSampler
importnumpyasnp
x=np.linspace(xmin, xmax, ngrid)
y=np.linspace(ymin, ymax, ngrid)
sampler=LintSampler((x, y), pdf)
pts=sampler.sample(N=100000)
在这个示例中,我们首先定义了两个维度的网格,然后将网格和概率密度函数
pdf
传递给
LintSampler
对象。最后,我们使用
sample
方法生成了100000个样本点。需要注意的是,这里的
pdf
函数并未给出具体定义,完整的示例可以在lintsampler文档中找到。
生成的样本点
pts
可以用散点图可视化:
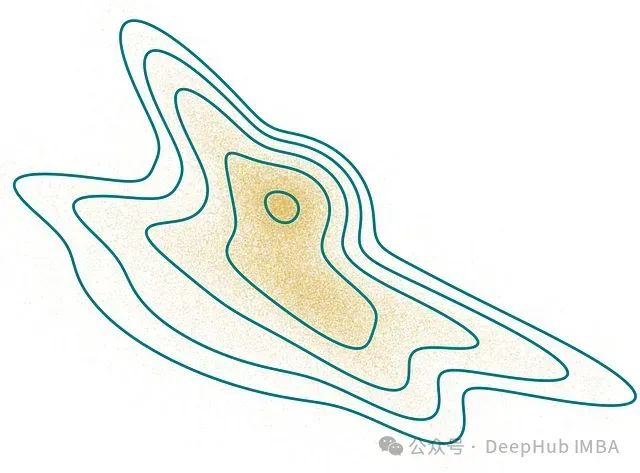
图2:从复杂PDF中抽样得到的点的散点图。背景等高线表示原始PDF。
这个例子展示了
lintsampler
使用的简便性。在某些情况下,它比MCMC或拒绝采样方法更快、更高效。
lintsampler的技术实现
如果你对
lintsampler
的内部工作机制感兴趣,本节将详细介绍其核心算法。如果你只关注使用方法,可以直接参考官方文档,其中包含了安装指南、使用说明以及多个维度(1D、2D、3D)的示例。文档还介绍了
lintsampler
的一些高级功能,如准蒙特卡罗采样(又称低差异序列)和自适应树结构采样。
线性插值采样算法
lintsampler
的核心是一种称为线性插值采样的算法,本节将概述其基本原理。
以下示例说明了当您将概率密度函数(PDF)和网格传递给
LintSampler
类时,
lintsampler
内部的处理流程。我们以二维高斯分布为例,但这种方法适用于任意维度和更复杂的PDF。
网格评估:首先,在给定的网格上评估PDF。下图展示了一个使用不均匀网格的例子:图3:左:2D高斯PDF。右:在不均匀网格上评估的PDF。(图片来源:作者)![]
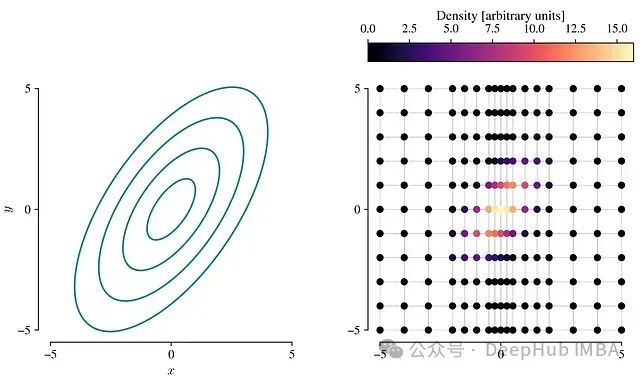
网格单元概率计算:利用梯形法则估计每个网格单元的总概率。计算方法为单元体积乘以其四个角点密度的平均值。
线性插值近似:在每个网格单元内,使用双线性插值近似PDF:图4:使用双线性插值填充的网格化PDF。![]![]
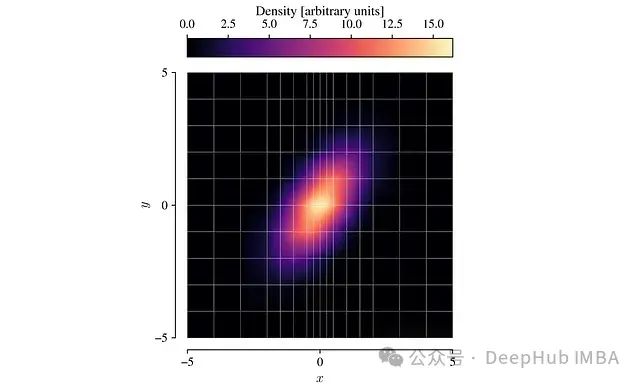
高效采样:基于线性近似的PDF可以高效地进行采样。单个样本的生成是一个两步过程:图5:左:随机选择的网格单元。右:在选定单元内采样的点。a. 首先,根据各单元的概率权重随机选择一个网格单元(如左图所示)。b. 然后,使用逆变换采样法在选定的单元内生成一个样本点(如右图所示)。
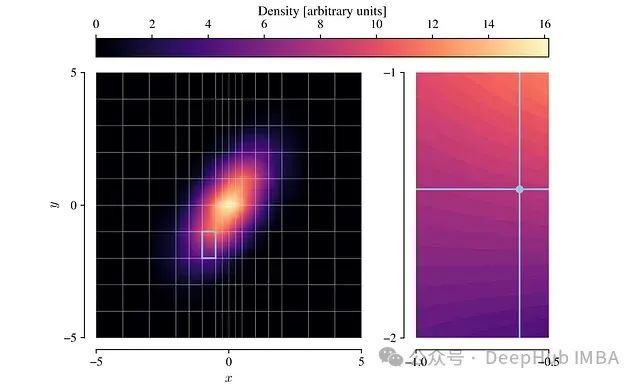
核心技术要点
线性近似是该算法的关键步骤。通过将每个网格单元内的PDF近似为线性函数,我们可以得到其分位数函数(即逆累积分布函数)的封闭解析形式。这使得逆变换采样可以简化为生成均匀分布的随机数并应用一个代数函数。
实际应用中,用户需要关注的主要参数是网格分辨率,以确保线性近似的精度足够高。适当的分辨率取决于具体的使用场景,
lintsampler
文档中的示例笔记本展示了不同情况下的最佳实践。
总结
lintsampler为从复杂概率分布中生成随机样本提供了一种简单、高效的解决方案。它结合了易用性和高性能,适用于广泛的科学计算和数据分析任务。对于需要处理非标准概率分布的研究人员和开发者来说,lintsampler是一个值得考虑的强大工具。
lintsampler主页和文档地址
https://lintsampler.readthedocs.io/en/latest/
作者:Aneesh Naik