如何检查时间序列是否平稳,如果它是非平稳的,我们可以怎么处理
当未来的数据与现在相似时,它更容易建模。平稳性描述了时间序列的统计特征不随时间变化的概念。因此一些时间序列预测模型,如自回归模型,依赖于时间序列的平稳性。
什么是平稳性?
平稳性描述了时间序列如何未来保持不变的概念。用数学术语来说,当时间序列的统计特性与时间无关时,它是平稳的,包括
- 均值不变(为常数)
- 方差不变
- 协方差与时间无关
这就是平稳性的弱形式的定义。另一种平稳性是严格平稳性。这意味着相同大小的样本具有相同的分布。由于严格平稳性具有局限性和罕见性,所以本文仅关注弱形式平稳性。
为什么平稳性很重要?
一些时间序列预测模型(例如,自回归模型)需要平稳的时间序列,因为它们更容易建模,因为它们具有恒定的统计属性。因此如果时间序列不是平稳的,就应该尽量让它平稳。
如何检验平稳性?
你可以用两种方法来测试时间序列的平稳性:
- 直观的方法:肉眼评估
- 统计方法:单位根检验
我们将创建几个示例,使用Hyndman 和 Athanasopoulos的时间序列分析教材《Forecasting: principles and practice》中提到方法解释平稳性的视觉评估,并扩展它们的用法,并解释使用单位根测试进行的平稳性测试。数据来自R的fma 包。
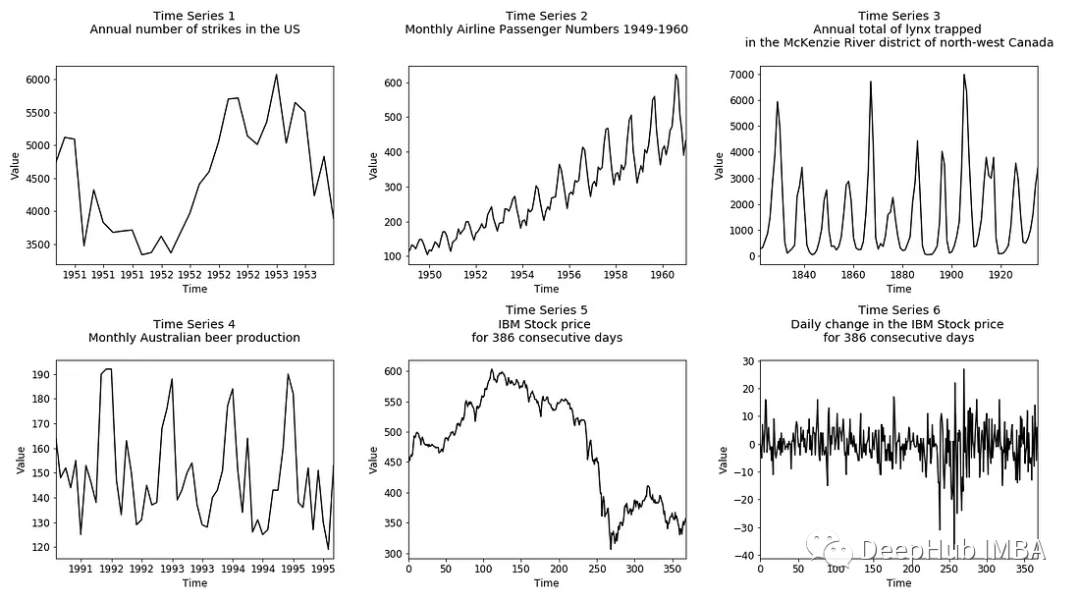
1、直观地评估平稳性
最简单的方法是将时间序列分成两半,并比较时间序列的前半部分到后半部分的平均值、振幅和周期长度。
- 均值常数-时间序列前半段的均值应该与后半段的均值相似。
- 方差常数-时间序列的前半段的振幅应该与后半段相似。
- 协方差与时间无关——时间序列前半部分的周期长度应该与后半部分的周期长度相似。周期应该在时间上是独立的(例如,不是每周或每月等)。
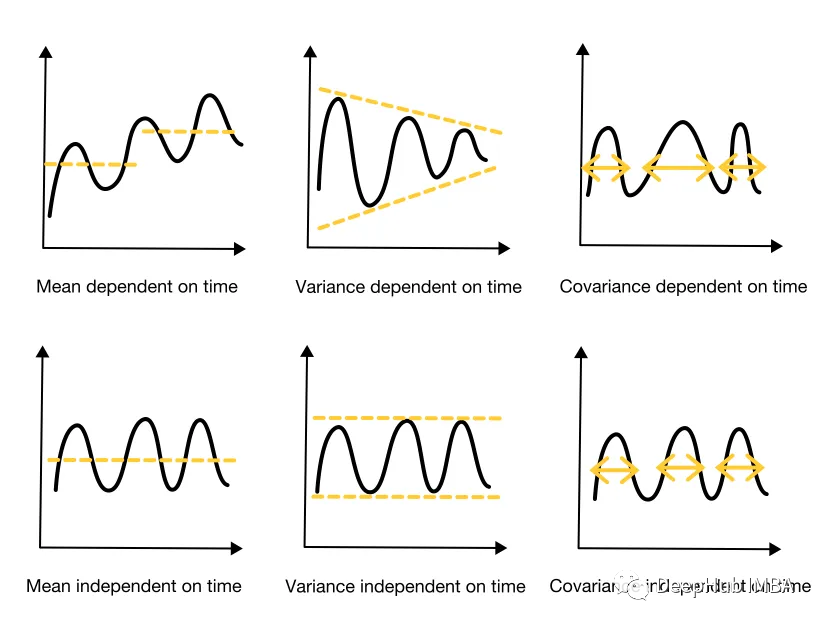
对于我们的例子,评估结果如下图所示:
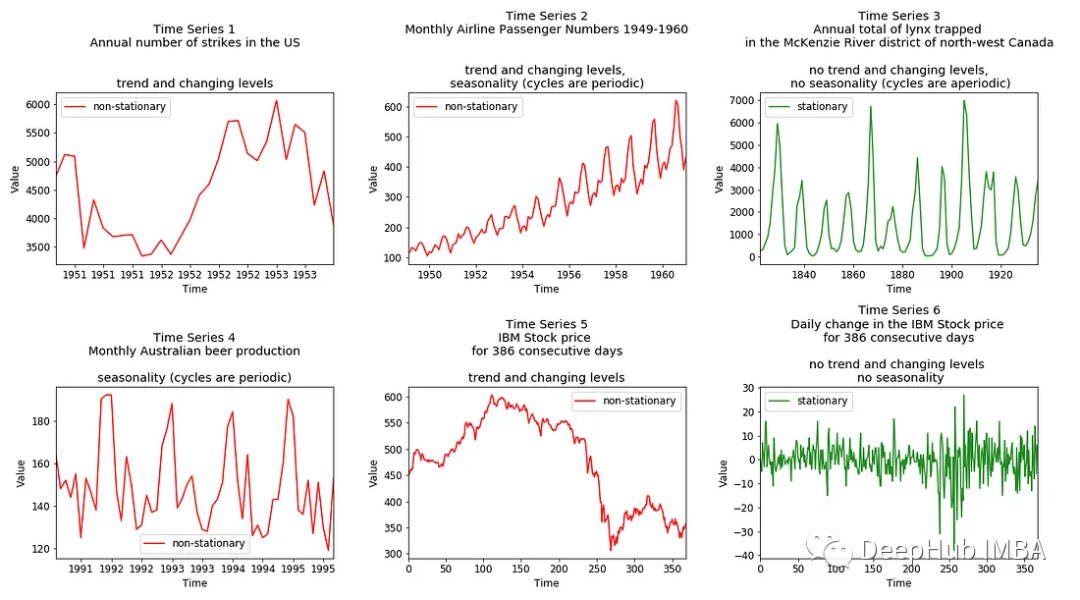
2、统计评估平稳性——单位根检验
单位根是一种随机趋势,称为“带漂移的随机游走”。由于随机性无法预测,这意味着:
单位根存在:不稳定(不可预测),单位根不存在:平稳的
为了用单位根检验平稳性,可以将两个这两个假设作为初始假设:
- 零假设(H0) -时间序列是平稳的(没有单位根存在)
- 备择假设(H1) -时间序列不是平稳的(存在单位根)
然后根据以下两种方法评估是否拒绝零假设:
p 值方法:
如果 p 值 > 0.05,则无法拒绝原假设。如果 p 值 ≤ 0.05,则拒绝零假设。
临界值法:
如果检验统计量没有临界值那么极端,则无法拒绝原假设。如果检验统计量比临界值更极端,则拒绝原假设。当 p 值接近0.05时,应使用临界值法 。
有几个单位根测试可以用来检查平稳性。本文将重点介绍最流行的2个:
Augmented Dickey-Fuller test 和 Kwiatkowski-Phillips-Schmidt-Shin test
3、Augmented Dickey-Fuller test
Augmented Dickey-Fuller test的假设为:
H0:时间序列不是平稳的,因为有一个单位根(如果p值> 0.05)
H1:时间序列是平稳的,因为没有单位根(如果p值≤0.05)
在Python中,我们可以直接使用statsmodels.tsa.stattools库中的adfuller方法。
from statsmodels.tsa.stattools import adfuller
result = adfuller(df["example"].values)
如果我们可以拒绝ADF检验的零假设,则时间序列是平稳的:
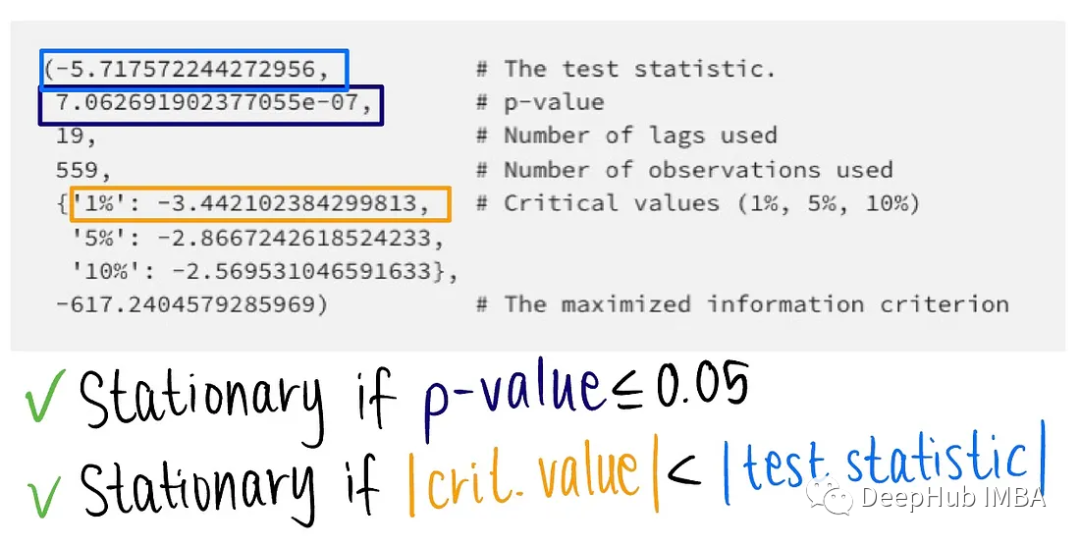
下面是样本数据集的ADF测试结果:
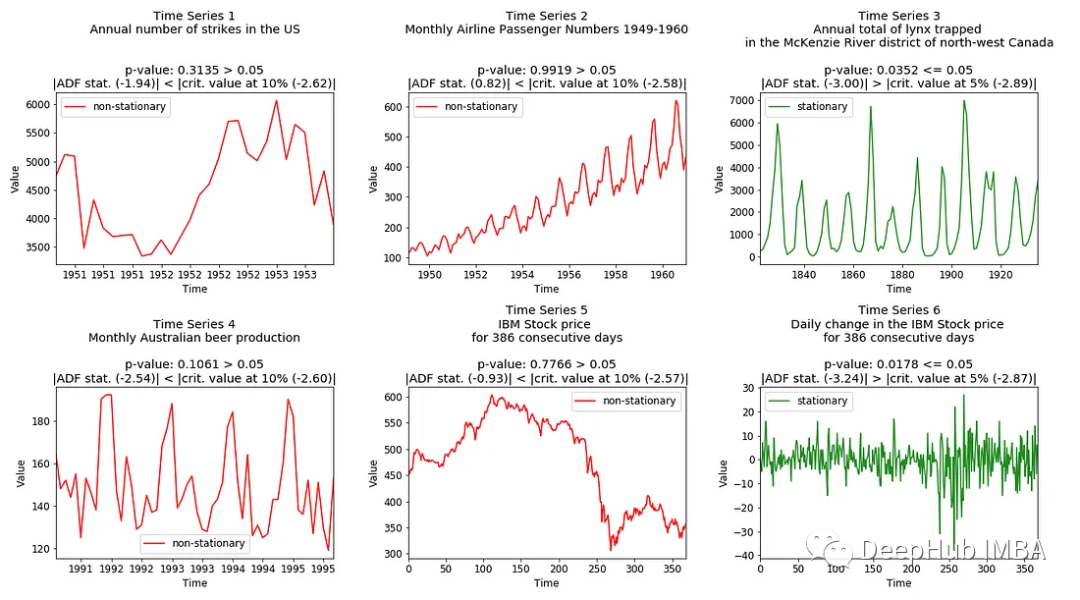
4、Kwiatkowski-Phillips-Schmidt-Shin test
Kwiatkowski-Phillips-Schmidt-Shin (KPSS)检验的假设是[4]:
H0:时间序列是平稳的,因为没有单位根(如果p值> 0.05)
H1:时间序列不是平稳的,因为有一个单位根(如果p值≤0.05)
statsmodels.tsa.stattools库中的kpss方法,我们需要使用参数regression = 'ct'来指定检验的零假设是数据是趋势平稳的。
from statsmodels.tsa.stattools import kpss
result = kpss(df["example"].values,
regression = "ct")
如果我们不能拒绝KPSS检验的零假设,则时间序列是平稳的:

下面是样本数据集的KPSS测试结果:
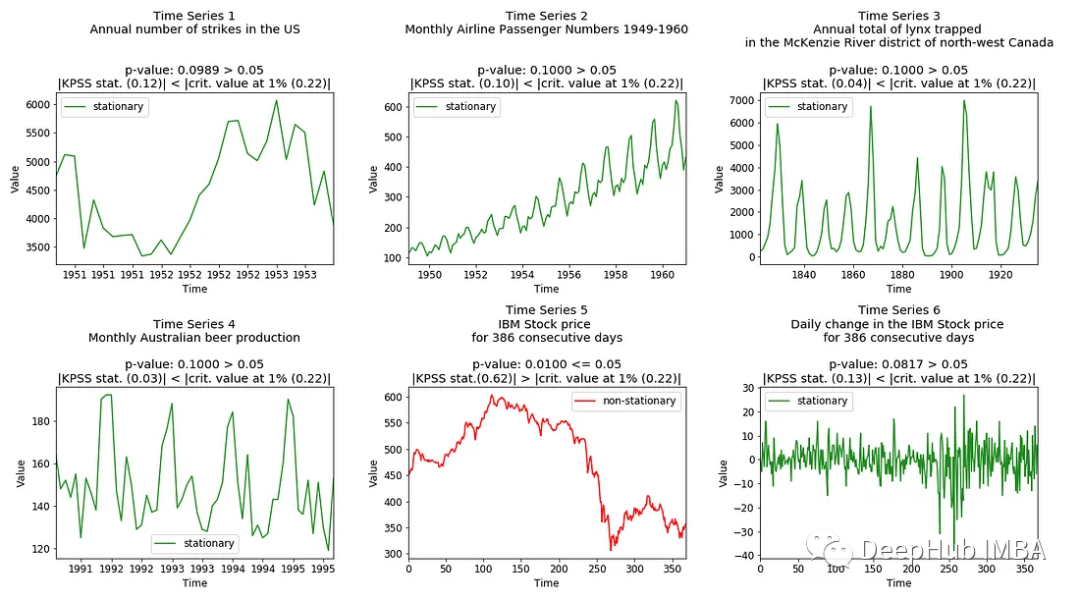
非平稳时间序列数据处理
我们可以对一个非平稳时间序列应用不同的变换,使其接近平稳:因为有几种平稳性类型,所以我们可以结合ADF和KPSS测试来确定要进行哪些变换:
- 如果ADF测试结果是平稳的,而KPSS测试结果是非平稳的,则时间序列是差分平稳的-对时间序列应用差分,并再次检查平稳。
- 如果ADF检验结果是非平稳性的,而KPSS检验结果是平稳性的,则该时间序列为趋势平稳的-需要去掉去趋势,并再次检查平稳性。
1、差分
差分计算两个连续观测值之间的差值。它稳定了时间序列的平均值,从而降低了趋势
df["example_diff"] = df["example"].diff()
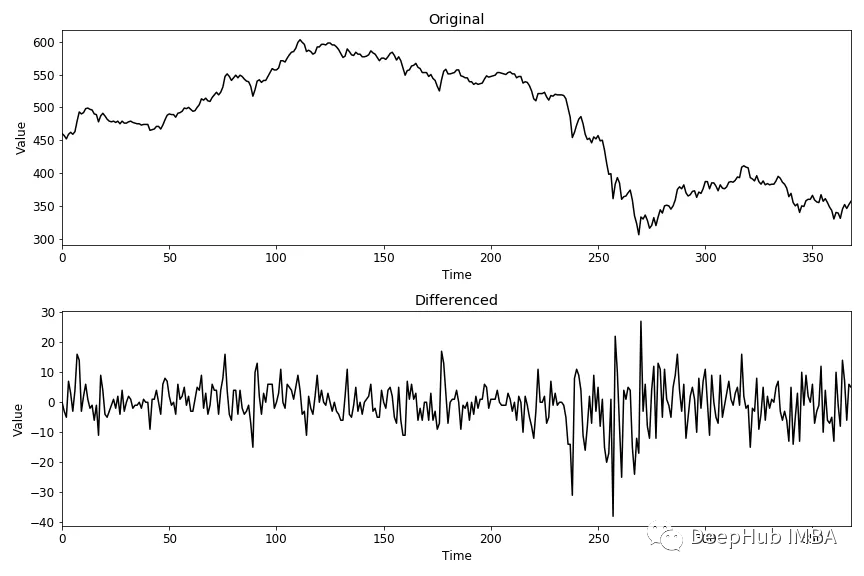
2、同过模型拟合去趋势
从非平稳时间序列中去除趋势的一种方法是将一个简单的模型(例如,线性回归)拟合到数据上,然后对该拟合的残差进行建模。
from sklearn.linear_model import LinearRegression
# Fit model (e.g., linear model)
X = [i for i in range(0, len(airpass_df))]
X = numpy.reshape(X, (len(X), 1))
y = df["example"].values
model = LinearRegression()
model.fit(X, y)
# Calculate trend
trend = model.predict(X)
# Detrend
df["example_detrend"] = df["example"].values - trend
结果如下:
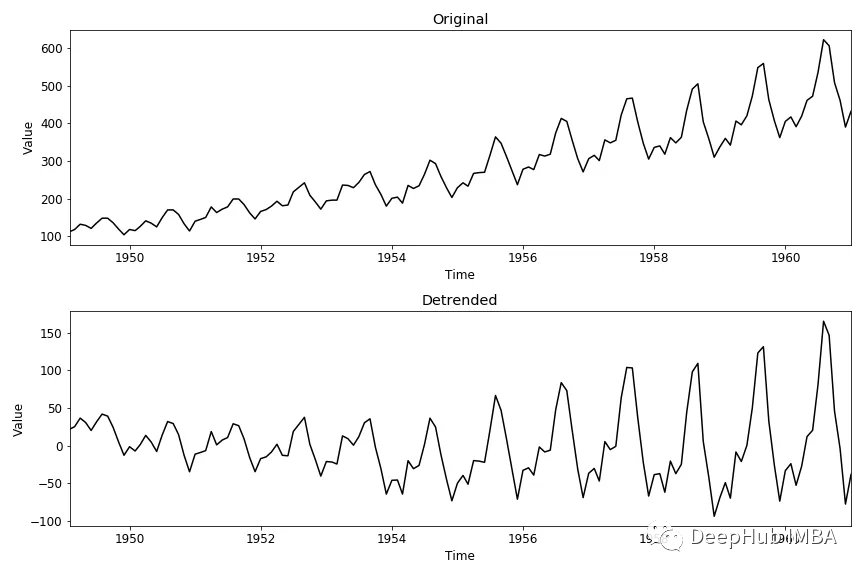
3、对数变换
对数变换可以稳定时间序列的方差。
df["example_diff"] = np.log(df["example"].value)
结果如下:
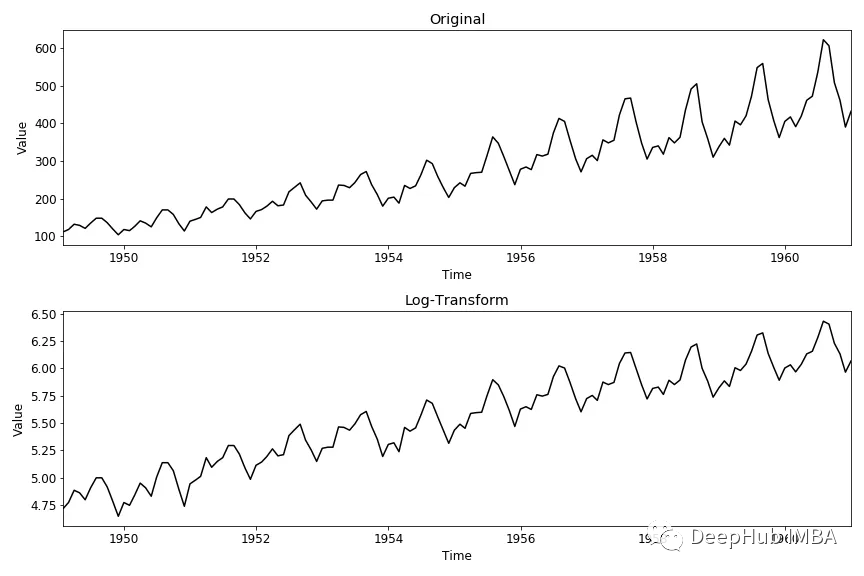
正如你所看到的,模型拟合的去趋势和对数变换都不能使我们的例子时间序列平稳。所以需要结合不同的技术使时间序列平稳。
总结
在时间序列预测中,具有恒定统计属性(均值、方差和协方差)且与时间无关的时间序列被描述为平稳的。由于稳定的统计特征,平稳时间序列比非平稳时间序列更容易建模。所以很多时间序列预测模型都假设了平稳性。
平稳性可以通过目测或统计方法进行检查。统计方法检查单位根,最流行的两种单位根测试是ADF和KPSS。这两种工具都可以在Python stattools库中找到。
如果时间序列是非平稳的,可以尝试通过差分、对数转换或去除趋势来使其接近平稳。
数据的R包是这个:http://pkg.robjhyndman.com/fma/
作者:Leonie Monigatti