什么是最大似然估计(MLE)
最大似然估计(Maximum Likelihood Estimation)是一种可以生成拟合数据的任何分布的参数的最可能估计的技术。它是一种解决建模和统计中常见问题的方法——将概率分布拟合到数据集。
例如,假设数据来自泊松(λ)分布,在数据分析时需要知道λ参数来理解数据。这时就可以通过计算MLE找到给定数据的最有可能的λ,并将其用作对参数的良好估计。
MLE是用于拟合或估计数据集概率分布的频率法。这是因为MLE从不计算假设的概率,而贝叶斯解会同时使用数据和假设的概率。MLE假设在计算方法之前,所有的解决方案(分布的参数)都是等可能的,而贝叶斯方法(MAP)不是这样,它使用了关于分布参数的先验信息。
MLE之所以有效,是因为它将寻找数据分布的参数视为一个优化问题。通过最大化似然函数,找到了最可能的解。
理解似然函数
顾名思义,最大似然估计是通过最大化似然函数来计算的。(从技术上讲,这不是找到它的唯一方法,但这是最直接的方法)。
似然函数是衡量样本成为观察到数据的概率。
如果数据集有1-n个独立同分布的(iid)随机变量,X₁至Xₙ,与观察到的数据 x₁ 到 xₙ 相关,我们就有似然函数的数学表达式:
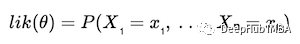
这可以很好地概念化似然函数——但是我们如何将其分解为可以从数据中计算出来的东西呢?换句话说,我们怎样才能找到最大化我们的似然函数的θ,并且确认他是最大化的?
给定
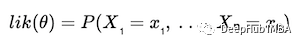
那么
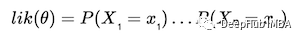
因为所有随机变量作为观察数据值的概率等于每个随机变量作为每个数据值的概率(因为它们是独立同分布的)。
最后,如果数据来自的分布具有密度函数 f(x),例如泊松分布,
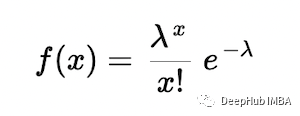
那么似然函数表示为
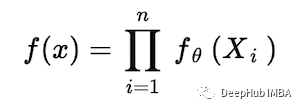
对于上面的泊松分布的例子,似然函数将是
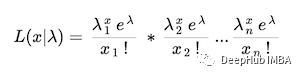
总之,似然函数是作为给定分布参数的函数给出的观测数据的联合概率。
如何最大化似然函数
现在可以用数学方式表达给定分布的似然函数,但看起来它是一个需要最大化甚至求导数的函数。那么如何有效地最大化似然函数呢?
取它的对数
虽然似然函数通常难以在数学上最大化,但似然函数的对数通常更容易处理。我们这样做的理论基础是:最大化对数似然的值 θ 也最大化似然函数。
泊松分布示例
我们继续使用上面已经建立的泊松分布作为示例。给定数据集X₁…Xₙ,这是i.i.d.,我们认为它来自泊松(λ)分布,λ的MLE是多少?分布中的λ参数的最大似然估计是什么?
总结一下,计算MLE的步骤如下:
- 求似然函数
- 计算对数似然函数
- 最大化对数似然函数
首先,我们已经建立了似然函数为
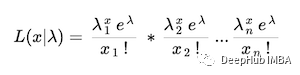
为了计算对数似然,我们取上述函数的对数。可以通过以下步骤推导:
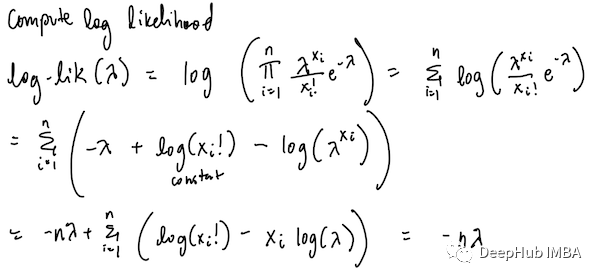
最后,我们最大化对数似然和简化,就得到最大似然λ。
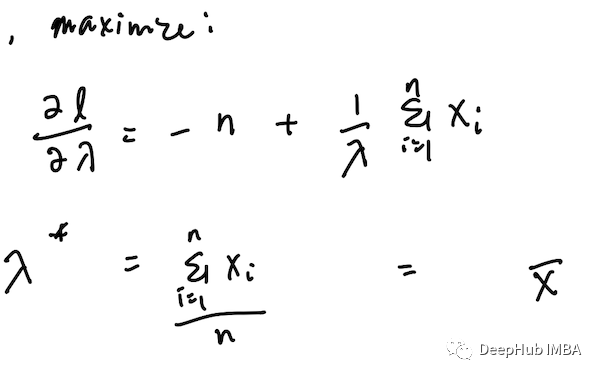
我们发现λ的最大似值是x的均值,或给定数据集x₁…xₙ的均值。
可以用MLE做什么
最直观的是给定数据集分布参数MLE,可以继续对数据集应用统计技术,并对数据集的确切分布做出假设。这样可以使统计分析更强大。除了数据集分布的估计参数外,MLE还有两个很有用的重要属性。
1、MLE 是它正在估计的参数的一致估计量。
参数θ的估计是一致的,如果
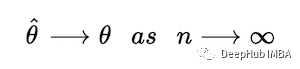
为什么会这样呢?因为大数定律。n很大,估计与θ相差很大的概率很小。
因为MLE是它所估计的参数的一致估计
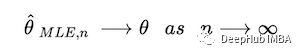
这告诉我们什么?数据集越大,MLE 估计越准确。
2、MLE 是渐近正态的
这意味着如果 MLE 估计器正在估计 θ₀(是参数 θ 的真实总体值),那么随着 n 增加到 ∞,
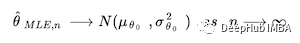
要查找µ和σ2,可以使用Fisher Information等其他技术,它告诉我们更多关于 MLE 本身的分布。但这超出了本文的范围。
总结
MLE 是一种技术,可以生成对要拟合数据的任何分布的参数的最可能估计值。估计值是通过最大化数据来自的分布的对数似然函数来计算的。本文解释了 MLE 的工作原理和方式,以及它与 MAP 等类似方法的不同之处。还解释了似然函数的定义以及如何推导它。最后还使用了一个从泊松分布计算 MLE 的示例,并解释了 MLE 的两个重要属性,即一致性和渐近正态性。希望这对任何学习统计和数据科学的人有所帮助!
作者:Edison