本文是关于检测和处理数据集中的异常值,主要包含以下四部分内容:
- 什么是异常值?
- 为什么检测异常值很重要?
- 如何检测异常值?
- 如何处理异常值?

什么是异常值?
异常值是与其他观察结果显着不同的数据点。如下图所示,橙色数据点与一般分布相去甚远。我们将此点称为异常值。
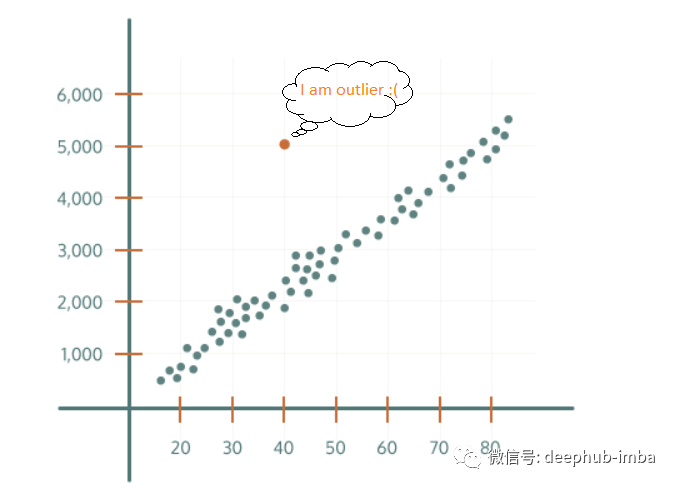
为什么检测异常值很重要?
在数据科学项目、统计分析、机器学习应用中检测异常值非常重要:
- 异常值会导致分布偏斜。
- 异常值会严重影响数据集的均值和标准差。这些可能会在统计上给出错误的结果。
- 可能导致偏差或影响估计。
- 大多数机器学习算法在存在异常值的情况下都不能很好地工作。
- 异常值在欺诈检测等异常检测中非常有用,其中欺诈交易与正常交易非常不同。
特别是在线性问题中,异常值更能显示出它们的影响。例如下面的例子;左边的图片中当 x 变量的值增加时,y 变量的值减小。但是由于异常值,观察到随着变量 x 的值增加,变量 y 的值也增加。异常值扭曲了我们的分析结果。

在上面的示例中,如果从数据集中移除异常值,可以获得更准确、不会被误导的测试结果。
如何检测异常值?
可以通过许多不同的方式检测异常值。下面总结了一些常用的方法:
- 领域的知识
- 标准差法
- Z-Score法
- 箱线图(四分位距 - IQR)法
领域的知识
借助行业知识,可以了解数据集中的哪个观察结果可能是异常值。例如; 假设一名房地产经纪人,平均房屋租金为 700 美元。如果房屋租金为 5000 美元,就可以说这是一个异常值。
标准差法
在统计学中,标准偏差是衡量一组值的变化量或离散度的量度。低标准差表示这些值趋向于接近集合的平均值,而高标准差表示这些值分布在更宽的范围内。
正态分布如下图所示。在正态分布中,数据应该在一个小范围的值内,高值和低值的异常值较少。
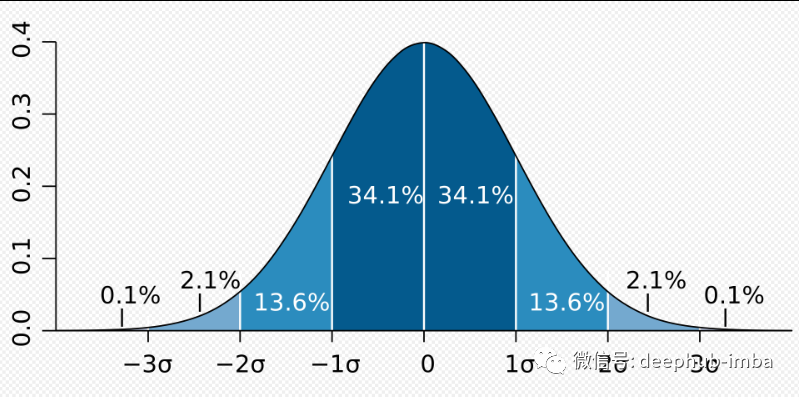
如图上图所示,
- 68.27% 的值在平均值的 +1、-1 标准差范围内,
- 95.45% 的值在平均值的 +2、-2 标准差范围内,
- 99.73 % 的值在平均值的 +3、-3 标准差范围内。
在正态分布中,预计我们的数据应该远离平均值 -3、+3 个标准差。因此,有了这些信息,可以指定下限和上限;
Lower Limit = Mean - 3 * Standart Deviation
Upper Limit = Mean + 3 * Standart Deviation
Z-Score法
Z-Score也称为标准分数。该分数有助于了解数据点与平均值之间的标准差。Z-Score是测量单位,它告诉我们数据点与平均值的距离。例如:数据点 A 与平均值相差 2 个标准差。这个 2 就是Z-Score。
Z score = (x -mean) / std. deviation
那么如何确定异常值的阈值呢?
下面再次检查正态分布以确定阈值。让我们看一下标准偏差方法部分中的正态分布图。正如上面前提到的,99.7% 的数据在正态分布的 -3、+3 标准差范围内,因此我们可以将超出此范围的数据点视为异常值。
如果上面语言比较难懂,用下面代码进行演示可能会更加直观:
# Suppose we have a dataset that represents number of siblings.
data = [1, 2, 2, 3, 4, 1, 1, 15, 2, 4, 3, 2, 1, 1, 2]
# In this data set we want to find outliers. Firstly we calculate Z-Score for them.
import numpy as np
mean = np.mean(data) # Find mean
std = np.std(data) # Find standart deviation
upper_limit = 3
lower_limit = -3
outlier = []
for i in data:
# Find Z-Score
z = (i-mean)/std
print(f'Z-Score of {i} = {z}')
# Check z value is within or not in our range
if (lower_limit > z) or (z > upper_limit):
outlier.append(i)
print('Outlier in dataset is', outlier)s
结果如下:

箱线图(四分位距 - IQR)法
在统计学中,四分位距 (IQR) 描述了从最低到最高排序的中间 50% 的数据。要找到 IQR,需要先将数据从最低到最高排序。然后将数据分成 4 个相等的部分,并指定 Q1、Q2、Q3 称为第一、第二和第三四分位数。IQR 是 Q3 和 Q1 之间的差。我们 50% 的数据介于这些四分位数之间。
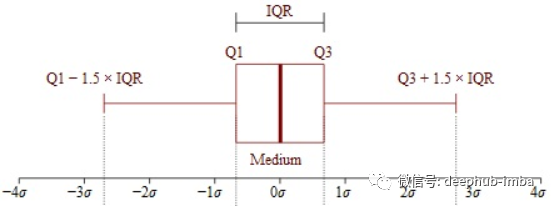
上图中:
- Q1 代表数据的第 25 个百分位。
- Q2 代表数据的第 50 个百分位。
- Q3 代表数据的第 75 个百分位。
例如我们有这样的数据:[1, 2, 2, 4, 5, 15, 6, 7, 8, 9, 10, 11, 17, 24, 33],我们想要找到 IQR。首先对这个数组进行排序;[1、2、2、4、5、6、7、8、9、10、11、15、17、24、33],然后我们找到四分位数;
Q1 25th , 4.5
Q2 50th , 8.0
Q3 75th , 13.0
计算IQR
IQR = Q3 - Q1
现在使用箱线图法用IQR 值计算上限和下限
Lower Limit = Q1 - 1.5 * IQR
Upper Limit = Q3 + 1.5 * IQR
之后,如果数据低于下限或高于上限,就可以将此数据点称为异常值。

如何处理异常值?
异常值可能是由于数据的内在可变性产生的,所以应该使用一些分析仔细检查这种类型的异常值, 另外的一些异常值可能是实验错误或数据输入错误等产生的,这些异常值是可以直接删除的。
删除值
如果异常值是由于输入或测量数据不正确,无法获得异常值的真实值,我们可以去除异常值。
例如在一个记录人们身高的数据集中,遇到了一个 1.8 厘米的数据。我们知道这在物理上是不可能的。可能真实身高 180 厘米、1.8 米或 185 厘米,但由于我们不知道是哪一个,所以可以将异常值删除。
修改值
如果包含异常值的行中的其他列包含重要信息,可能删除该行不是一个很好的选择,所以可以将异常值替换为阈值或中值(异常值对中值影响不大)。
异常值的对数转换
对数转换,就是将每个变量 x 都替换为 log(x),其中对数的基数被认为是常见的使用基数 10、基数 2 和自然对数 ln。
而对数转换与异常值有什么关系呢?
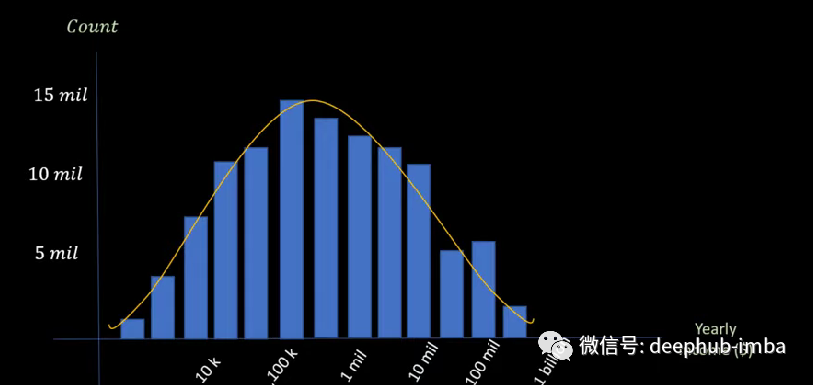
当异常值是由于数据的内在可变性引起的,我们可能不想删除或替换它们。因为这些是我们可能需要的数据。但是由于这些异常值,我们无法获得正态分布,得到的是偏态分布。例如,一个包含人们收入数据的数据集。虽然大多数人的收入在 30k 到 100k 之间,但有些人赚了数十亿美元。当可视化这样一个数据集时,观察到的分布向右倾斜。
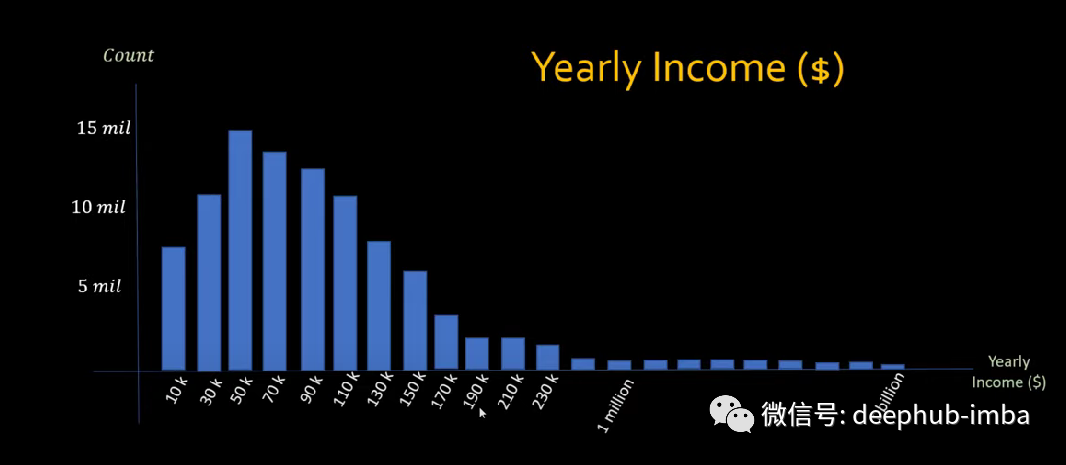
在这种情况下,对数转换可以帮助我们。对数变换不再强调异常值并允许我们潜在地获得正态分布。在上图中的 X 轴上应用对数函数,则偏态分布接近正态分布。
在应用对数转换之前,应该需要再次考虑下是否需要, 因为如果每个变量之间的距离很重要,那么取变量的对数会使距离倾斜,可能产生更大的问题。
使用其他模型
我们可以使用基于树的方法,如随机森林、决策树,因为树型方法只考虑值得分割点,而不考虑两个值之间得距离,所以相比于线性模型受异常值影响较小。
总结
本文介绍了异常值的相关知识,还有如果检测、处理异常值,在阅读完本文以后,希望你对异常值有一个大概的了解,并且能够检测和处理一般情况下遇到的异常值。
作者:Mert Yüksek