[因果推断] 增益模型（Uplift Model）介绍（三）

一 基础介绍

增益模型（uplift model）：估算干预增量（uplift），即干预动作（treatment）对用户响应行为（outcome）产生的效果。

这是一个因果推断（Causal Inference) 课题下估算ITE（Individual Treatment Effect）的问题——估算同一个体在干预与不干预（互斥情况下）不同outcome的差异。为了克服这一反事实的现状，增益模型强依赖于随机实验（将用户随机分配到实验组&对照组）的结果数据。

二 因果推断基础

1. Causal Discovery，即因果关系的挖掘；

2. Causal Effect Estimation，即因果效应的估计

ITE（Individual Treatment Effect）表示一个individual的treatment effect。那么如果我们想看一个大群体（一个普遍现象），就是**ATE(average treatment effect)啦，ATE is the expectation of ITE over the whole population i=1,...,n：那么介于两者中间呢，就有一个CATE(conditional average treatment effect)**，也就是一个subpopulation的average treatment effect。其实ITE就是CATE的变种，只不过这个subpopulation缩小到了一个人。

注意到，我们想要的是某个个体给券不给券的区别，而不是总体给券不给券的区别，所以这里就不是研究ATE（average treatment effect），而是研究ITE（individual treatment effect）。而由于我们是使用observational data，ITE是CATE的一个特殊情况，我们其实研究的是CATE：an average treatment effect specific to a subgroup of subjects, where the subgroup is defined by subjects' feature。举个例子：如果我们的特征包括性别，年龄，职业，app活跃度。那我们其实想知道的是：一个app活跃度高的30岁男性程序员给券和不给券对购买概率的差异。

而这里CATE模糊来讲，就是heterogeneous treatment effects。因为他认为总的population是heterogeneous的，所以我们要通过X来区隔出一个个subpopulation。于是我们成功从uplift模型过渡到了一个研究heterogeneous treatment effects的问题 (为了后续行文方便，heterogeneous treatment effects我们有时候会写成treatment effects或者CATE或者ITE，都理解为一个东西就好)。

Propensity Score

这里再介绍一个有用的概念——倾向分（propensity score），即给定 Xi 用户被干预的概率

三 什么是Uplift模型

Response Model：预测用户看过广告之后转化的概率，不区分自然转化人群（即有些用户即使不用广告触达也会转化）；

Uplift Model：预测用户因为广告而购买的概率，这是一个因果推断的问题，帮助我们定向营销敏感人群，预知每个用户的营销敏感程度，从而制定差异化营销策略，促成整个营销的效用最大化。uplift概念：the effect of an action on some customer outcome

用一个简单的例子来介绍此模型。假设电商平台，一件标价500元的商品，用户的购买率为5%。现有一批预算可以给用户发放20元的优惠券以提升用户购买率。需要给每个用户都发放优惠券吗？答案显然是否定，那么这批优惠券应该发送给平台的哪些用户呢？此时我们脑海中有四类用户：

• Persuadables：不发送优惠券则不买，发送优惠券则购买；
• Sure things：不论是否发送优惠券均会购买；
• Lost causes: 不论是否发送优惠券均不会购买；
• Sleeping Dogs: 不发送优惠券会购买，发送优惠券反而不买；

1. Persuadables(说服型)类用户被发券后产生了正向变化，从不买转化为购买，干预后购买率得以提升，此部分是我们真正想要进行触达干预的营销敏感用户。

2 Sure things(确认型)类用户以及3 Lost causes(沉睡型)用户无论是否发券均不会改变其原本的购买行为，对这部分用户发送优惠券则会造成资源浪费。

4 Sleeping Dogs(勿扰型)用户对营销可能相对反感，干预会产生反效果，这类用户我们尽量避免打扰。

Uplift模型要解决的问题就是通过建模预测的方法精准的去对这四类用户进行分群。我们获取到的训练训练数据是不完整的，对于单个用户来说，不可能同时观测到在有干预(发券)和没有干预(不发券)两种情况下的表现，这也是因果推断中的反事实的问题。

可以从用户的角度来对平均因果效应做估计，假如我们有两组同质用户，对其中一组用户发券，另外一组不发券。之后统计这两群人在购买转化率上的差值，这个差值就可以被近似认为是可能的平均因果效应。Uplift建模需要服从CIA条件独立假设，最简单的解决方式就是A|B TEST实验，因为样本在特征上分布较为一致，因此随机实验是Uplift Model建模过程中非常重要的前置条件。若随机实验下各个类别用户组数量性质较相似，则此Uplift模型即可较精准的预测给用户发放优惠券的收益。

• 首先，我们选取部分用户(小流量实验，样本量足够建模)随机分为实验组和对照组，对照组不发优惠券，实验组发放优惠券，用户最终是否购买为一个0-1变量；
• 然后，对整体实验数据用户购买行为进行建模；
• 最后，再用小流量实验训练得到模型对我们需要预测的全量用户进行条件平均处理效应估计，预测其发放优惠券所带来的增益值；

假设有N个用户，用户i在没有优惠券的购买结果为Yi(0)，在有优惠券时购买结果为Yi(1)，此时发送优惠券对该用户的增益就是uplift score (i)=Yi(1)-Yi(0)。当uplift score为正值时，说明干预项对用户有正向增益作用，也就是上文所提到的Persuadables(说服型)用户。

注意一般的预测模型是预测这个人给券后的购买概率，这不是我们要的，我们要的是这个人给券比不给券购买概率的增量

response模型 VS uplift模型

response模型的目标是估计用户看过广告之后转化的概率，但是我们没有办法从中区分出自然转化人群。

uplift模型则是估计用户因为广告而购买的概率，这是一个因果推断的问题，帮助我们锁定对营销敏感的人群。

比如某次广告曝光，用户B的转化概率大于用户A的转化概率，这种时候你可能会认为用户B受这次营销的影响更大。其实这样是不合理的，因为忽略了用户的自然转化概率，转化率高的用户可能是自然转化率本身就比较高，但是他的uplift值并不一定高。也就是说要真正归因到营销广告带来的效果，应该从uplift的角度出发。uplift模型能够直观知道哪个用户最有可能受事件干预影响，最终可通过向这类用户制定营销方案，以保证在活动预算有限的情况下，提升整体的用户转化效果。

四 建模方法

在建模前我们需要注意一个很重要的问题：Uplift Model对样本要求很高，需要用户特征和干预策略相互独立。

那么什么样的样本用户有这样的特征，这样的样本又该如何获取？

最简单直接的方式就是随机A/B实验，A组采用干预策略，B组不进行任何干预，经过A组和B组的流量得到的两组样本在特征分布上基本一致（即满足CIA）

可以通过模拟两组人群的T 而得到个人用户的t 因此随机A/B实验在Uplift Model建模过程中至关重要，在训练样本高度无偏情况下，模型才能表现出更好的效果。

在快速发展中，Uplift形成了三种主要的实现方式

传统倾向模型

这实际上不是Uplift模型，但由于它是解决Uplift问题的经典方法，因此需要包括在内。该算法通常是类似于逻辑回归的分类器。这些算法输出0到1的概率，用于对受众进行分类。然后选择一个阈值（可能为0.7或更高）作为用户分群的临界值。

Uplift模型

此方法可以直接对治疗效果进行建模。它要求对随机森林这样的算法进行重新设计，以实现特征选择，超参数调整，并适合解决给定（x）的（t）对（y）的影响等功能。但是目前Scikit-learn里的随即森林无法实现上述功能。需要使用软件包R for Up和Python CausalML来实现对应的提升树

1、差分响应模型 Two-Learner Method

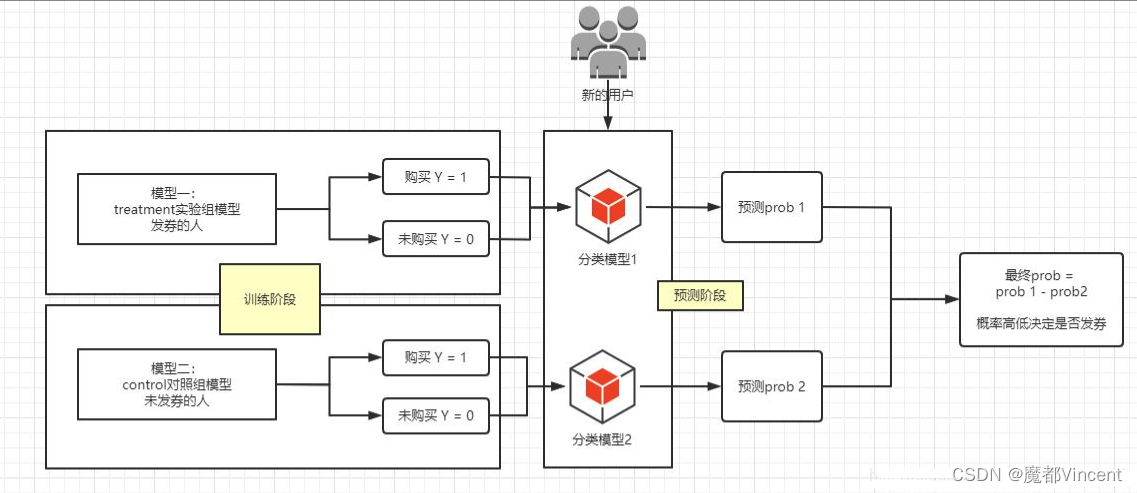
最简单粗暴的建模方法是基于Two Model的差分响应模型，对A组和B组数据进行单独建模,我们对实验组(有干预)和对照组(无干预)的购买行为进行分别建模，然后用训练所得两个模型分别对全量用户的购买行为进行预测，此时一个样本用户即可得出有干预和无干预情况下两个购买行为预测值。这两个预测值的差就是我们想要的uplift score。这种建模方法较简单且易于理解，可以复用常见的机器学习模型(LR、Tree Model、NN)

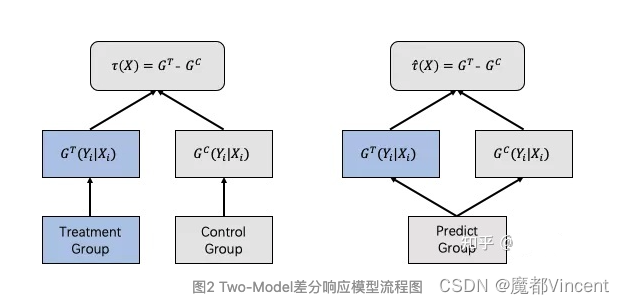
其中模型用来学习用户在有干预策略影响下的响应，另外一个模型用来学习用户在没有干预策略下的响应，对于预测组数据，分别过两个模型，将得到的模型预测分数做差，就得到uplift score。

一些局限性：

• 对照组和实验组分别建模，两个模型完全隔离，可能两个模型各有偏差从而导致预测的误差较大。其次建模的目标是Response而不直接是Uplift，因此模型对Uplift的预测能力较有限；
• 策略只能是离散值，不能是连续变量，因为有几种策略就需要建几个模型。所以当干预条件只有‘是否发优惠券’时，此建模方法可行，但是当涉及到‘多种优惠券面额/文案组合策略’或者‘发多大面额优惠券这种连续变量策略’时，本种建模方法可能并不非常work；

在实际中以uplift score进行排序，由其高低决定是否进行干预。虽然两个模型单独训练容易累计误差传递到uplift score，但是考虑到实现简单迅速，可以将其作为baseline。

2、差分响应模型升级版 **Single-Learner Method **

Single-Learner在Two-Learner的基础上，将对照组数据和实验组数据放在一起建模，使用一个模型对处理效果进行估计，然后计算该样本用户进入实验组和对照组模型预测的差异作为对实验影响的估计。与Two-Learner不同的是，本模型将实验分组（干预项）作为一个单独特征和其他变量一起放入模型中对用户购买行为进行建模，干预项可以是多种组合策略或者连续变量。

训练样本共用可以使此模型学习更加充分，通过单个模型的学习也可以避免双模型打分累积误差较大的问题。此外模型可以支持干预项为多策略及连续变量的建模，实用性较强。但此模型在本质上依然还是对Response建模，对Uplift的预测还是比较间接

基于Two Model的差分响应模型，训练数据和模型都是相互独立，那么是否可以进行模型统一和数据共享呢？答案是肯定的，那就是基于One Model的差分响应模型，那么问题来了，数据共享、模型统一，怎么学习干预组合非干预组样本的差异呢？在阿里文娱中提到一种方法：在特征维度进行扩展，引入干预信号相关特征T（T为0代表干预组，否则为非干预组，T同样可以扩展为0-N，建模multiple-treatment问题，比如优惠券的不同额度，广告的不同素材）

单模型相比双模型的方式有以下几个优势：

• 模型训练时数据利用更充分.
• 建模更加简单，只需要一个简单的逻辑回归或树模型(随机森林、Xgboost、Lightgbm).
• 能对处理变量或者其他变量进行强制的单调约束，双模型无法做到这一点.

优点 - 训练样本的共享可以使模型学习的更加充分 - 同时通过模型的学习也可以有效的避免双模型打分误差累积的问题 - 从模型的层面可以支持multiple treatment的建模，具有比较强的实用性。

缺点 - 同时和Two Model版本类似，它的缺点依然是其在本质上还是在对response建模，因此对uplift的建模还是比较间接，有一定提升的空间。

3、标签转换模型 Class Transformation Method

即使基于One Model的差分响应模型在训练数据和模型层面上打通，但其本质还是对于uplift的间接建模，更为严谨的一种实现实验组和对照组数据和模型打通的方法是：标签转换方法（Class Transformation Method），可以直接对τ()进行建模。

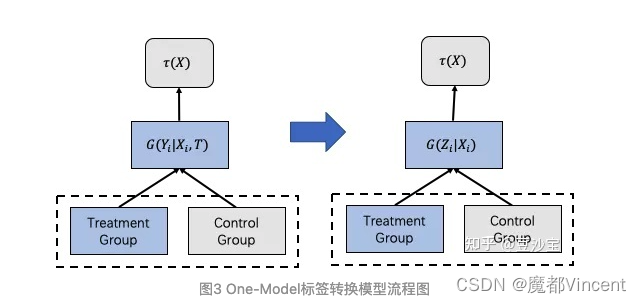
Class Transformation Method模型既可以将实验组与对照组数据打通，同时它又是直接对Uplift score进行预测，计算用户在实验组中购买概率与在对照组中购买概率的差值，其核心思想是将实验组和控制组样本混合并创建新的变量z满足：

• 当用户在实验组(发券)且用户最终购买时，z=1
• 当用户在对照组(无干预)且用户最终未购买时，z=1
• 当用户在实验组(发券)且用户最终未购买时，z=0
• 当用户在对照组(无干预)且用户最终购买时，z=0

可以证明，P(Z=1│Xi) 和Uplift Score是线性正相关的，且当实验组与控制组样本比例为1:1时，Uplift Score =2P(Z=1│Xi)-1，目标从预测Uplift Score转化为了预测P(Z=1│Xi)

该方法适用于Treatment和Outcome都是二类分类的情况，通过将预测目标做单类的转换，从而实现单模型预测。

元学习 -- Meta-learner Methods

A meta-algorithm (or meta-learner) is a framework to estimate the Conditional Average Treatment Effect (CATE) using any machine learning estimators (called base learners)。

就是这类算法直接用machine learning model作为基学习器来学习，比较简单。

Meta-Learning方法是指基于Meta-Learner进行Uplift预估，其中Meta-Learner可以是任意的既有预测算法，如LR、SVM、RF、GBDT等。根据Meta-Learner的组合不同，

通常分为：S-Learner、T-Learner、X-Learner、R-Learner。

【优点】：利用了既有预测算法的预测能力，方便易实现。

【缺点】：不直接建模uplift，效果打折扣。

**4.1 S-learner **

Conditional Outcome Modeling （COM）

这个模型最简单，直接把Treatment作为特征放进模型来预测

论文地址：https://arxiv.org/pdf/1706.03461.pdf

S-Learner是指单一模型，把对照组和实验组放在一起建模，把营销动作作为一个特征（如将对照组），特征加入训练特征，如下图所示。在预测时，改变不同的W值计算相应率，从而与对照组相减得到uplift score。

S-Learner方法简单，且也可以使用常见模型作为基模型如XGBoost、LightBGM和NN等，但其本身仍然是响应模型，模型的效果取决于特征W的贡献度，若W的贡献度较低，则有可能会被模型过滤，导致Uplift Score为0。

存在问题：当数据纬度变大时，容易产生估计偏差 (estimate biased towards 0！），这个很直观，假设数据有100维，T只是其中1维，模型训练时容易忽略这个维度，导致计算出来ATE -> 0

S-learner是将treatment作为特征，干预组和非干预组一起训练，解决了bias不一致的问题，但是如果本身X的high dimension可能会导致treatment丢失效果.

【优点】S-Learner简单直观、直接使用既有预测算法；预测仅依赖一个模型，避免了多模型的误差累积；更多的数据和特征工程对预测准确率有利。

【缺点】但是该方法不直接建模uplift；且需要额外进行特征工程工作(由于模型拟合的是Y，所以若W直接作为一个特征放进去，可能由于对Y的预测能力不足而未充分利用)。

【应用】在因果推断未受关注之前，诸如”优惠券“发放的问题常用该方法，直接建模”对什么人，发放什么面额券，是否会下单“，预测阶段则对User和Coupon交叉组合后进行预测，得到(User,Coupon)组合的下单率，然后再依据预算、ROI或其他约束进行MCKP求解。

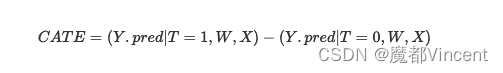
这里的y.pred就是模型的预测值

4.2 T-learner

Grouped COM (GCOM)

（Two Model）是将对照组和实验组分开建模，然后实验组模型与对照组模型响应概率的差即为提升值。论文地址：https://arxiv.org/pdf/1706.03461.pdf

这个模型不同于上一个，先对于 T=0 的control组和 T=1的 Treatment组分别学习一个有监督的模型。control组模型只用control组的数据，Treatment组模型只用Treatment组的数据。

    在多实验场景中，如优惠券金额有多种，是将不同的实验组模型与对照组模型做差，得到不同动作下的uplift socre，然后，在根据不同约束从中选择最合适的动作。

  T-Learner方法具简单直观，但同时模型对样本利用不充分，对照组和实验组模型无法利用对方样本，且双模型存在累积误差，对数据不平衡响应较大

存在问题：每个estimator只使用部分数据，尤其当样本不足或者treatment、control样本量差别较大时，模型variance较大（对数据利用效率低），我们需要提升数据利用率！

【优点】T-Learner一样简单直观、直接使用既有预测算法；将不同的数据集中的增量效果转换为模型间的差异，不需要太多的特征工程工作；当有随机试验的数据时该方法作为baseline很方便。

【缺点】该方法存在双模型误差累积问题；同时当数据差异过大时(如数据量、采样偏差等)，对准确率影响较大。

简单来看，这里会构建两个模型，treatment / control 两个：

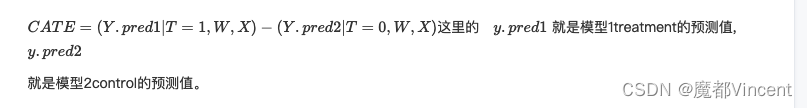
4.3 X-learner

X-Learner是在T-Learner的基础上优化的一种方法，利用了全量的数据进行预测，且对于Treatment和Control样本不平衡时，也有较好的效果

论文地址：

https://arxiv.org/pdf/1706.03461.pdf

类似上一个，先对于 T=0 的control组和 T=1的 Treatment组分别学习一个有监督的模型。control组模型只用control组的数据，Treatment组模型只用Treatment组的数据。

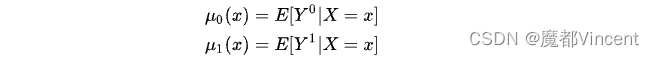
X-Learner在T-Learner基础上，利用了全量的数据进行预测，主要解决Treatment组间数据量差异较大的情况。但流程相对复杂、计算成本较高，有时还会由于多模型误差累积等问题效果不佳。 另外，不论是分类问题还是回归问题，在 计算最终效应步骤时，都需要使用回归模型来拟合。

理解：对Step3中，若W=1的比例极小，则 g(x) 极小，则 的权重更大，即更倾向于使用 的结果，也即倾向于control组数据训练的模型。

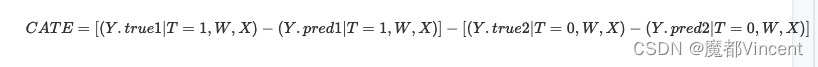
这里的 y.pred1 就是模型1treatment的预测值与实际值，y.pred2 就是模型2control的预测值与实际值。

五 Uplift模型评估

根据Uplift Score的定义，分数越高的用户即所谓的营销增益就越大。增益模型由于不能同时观测同用户在不同干预项下的真实增量，通常是通过划分十分位数来观测实验组用户和对照组用户样本来进行间接评估。

难点：不存在ground truth——因为无法同时对一个样本干预和不干预。

因为上述难点，大部分衡量指标需要通过聚合指标（衡量群体）实现，例如uplift bins和uplift curves.

1、Uplift 十分位柱状图 uplift bins

一种常见做法如下：

1. 对所有样本（包括实验组和对照组）同时预测uplift值
2. 按照uplift值排序，计分别算每个十分位里实验组和对照组的outcome平均值
3. 计算每个十分位两组平均值的差

将测试集预测出的用户按照Uplift Score由高到低平均分为10组，分别是top 10%用户，top 20%用户……top 100%用户。分别对每个十分位内的用户求实验组和对照组预测分数的均值，然后相减，计算不同分段中真正的实验提升收益。然后根据每个分组得出的实验收益，绘制十分位柱状图。这样，即可较直观观察到有多少的用户大概可以获得多少的营销增益。

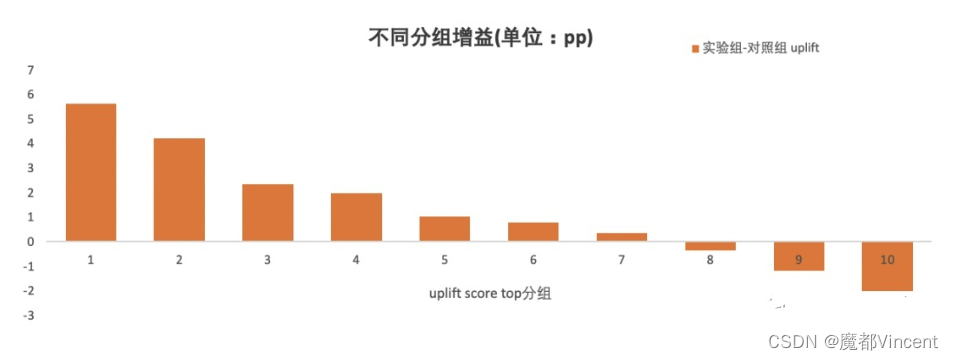
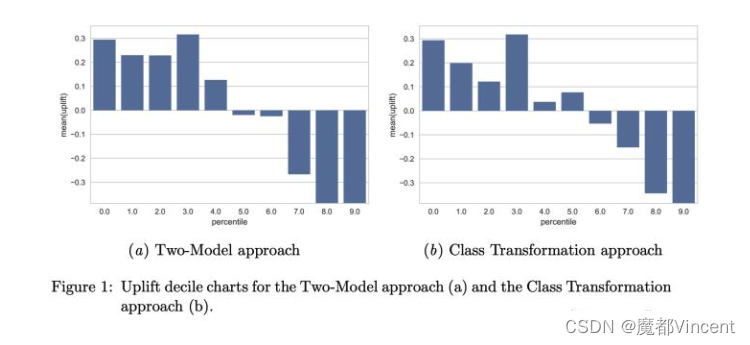
上图存在问题：无法比较两个不同模型的好坏

**2 **Cumulative uplift/gain

Cumulative uplift：通过计算topK组内Treatment和Control组的 y差值，可以表达在topK组得分的数据内，增量效果如何。如左图。

Cumulative gain：一些场景中，我们需要的不只是按照”uplift“选中部分的效果，而需要的是根据”uplift“来决策是Treat还是Control之后，能够带来的增量绝对量有多少。如右图，此时选择最高点即为最佳效果，再往后的实际是Control组优于Treatment组的部分。

为了能跨模型比较，我们引入累积增益图：第一个bar代表前10%的uplift，第二个bar代表前20%的uplift。一个表现好的模型在前半段会有比较大的值，后半段下降。

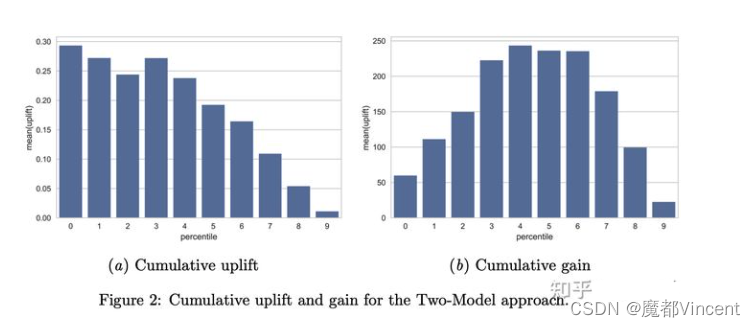
Cumulative Gain：计算uplift值乘以每个bin的总人数（图(b)）

其中 和 分别代表实验组中响应的总人数和实验组的总人数，对照组同理。

图(b)对运营的同学很有用：如果希望圈选一部分人进行干预，可以通过图找到增益效果的最大值（例：圈选前40%的用户可以达到最大值）

3 qini曲线(qini curve)

计算每组用户百分比的qini系数，将这些系数连接起来，得到一条qini曲线。qini系数公式如：

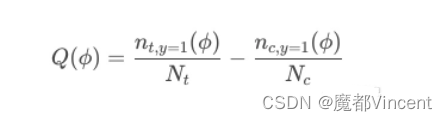
• ϕ是按照Uplift Score由高到低排序的用户数量占实验组或对照组用户数量的比例，ϕ = 0.3即表示实验组或对照组中前30%的用户。
• nt,y=1(ϕ)表示在前百分比多少用户中，实验组中预测结果为购买的用户数量。nc,y=1(ϕ)表示在同样百分比用户中，对照组预测结果为购买的用户数量。
• Nt和Nc则分别代表实验组和对照组总用户样本数。

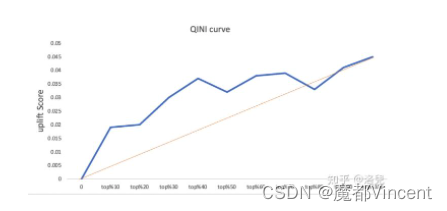
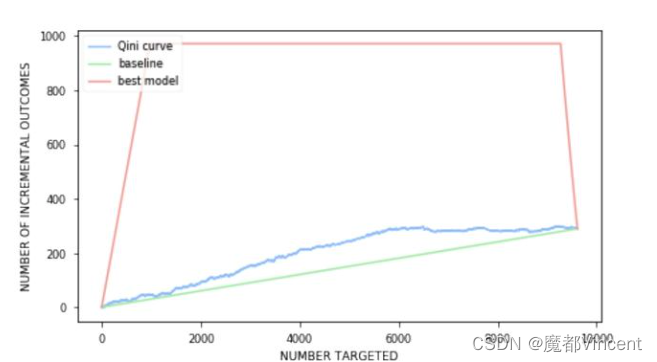
上图橙色线是随机曲线，qini曲线与随机曲线之间的面积作为评价模型的指标，面积越大表示模型结果远超过随机选择的结果。

可以看到当横轴为top40%时，qini曲线与随机曲线之间距离最大，对应的纵轴大概是0.037，表示uplift score等于0.037可以覆盖前40%的用户数量，这部分用户也就是我们可以对其进行营销干预的persuadable用户。但如果实验组和对照组用户数量不平衡，则会导致指标失真。另一种累积增益曲线可以避免这个问题。

Adjusted Qini

是为了避免实验组和对照组数据不均衡而导致Qini系数失真而设计的。计算方式如下：

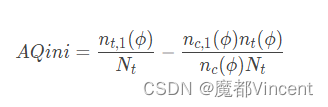
**累积增益曲线（Cumulative Gain curve） **

4、Uplift Curve & AUUC

上述方法还缺乏有效的度量手段，我们将数据集分组不断细分，精确到每个样本维度时，每次计算截止前t个样本的增量时，则得到Uplift Curve。公式如下

其中 t 表示按预测uplift值进行排序的前 t个观察值

可视化如下，其中x轴为样本位序，y轴为累积增量数量。上方的每条曲线表示按照uplift score降序排列后，累积的增量效果；random直线表示随机排序(随机选择样本执行Treatment时)的增量效果；每条曲线终点相交，表示全量Treatment时的平均增量效果。

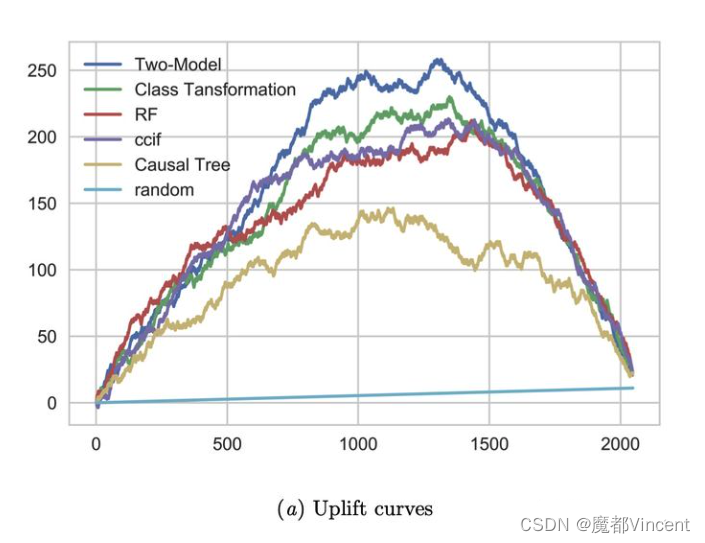
曲线中，越高拱的模型效果越好，数值化表示的话可以使用曲线下面积，与二分类评估中的AUC(Area Under ROC Curve)类似。这里称为AUUC(Area Under Uplift Curve)

基于上图，我们可以得到 uplift model 最常用的评估指标AUUC（Area Under Uplift Curve），即曲线下的面积。

5 Qini Curve & Qini Coefficient

上述Uplift Curve存在一个问题，当Treatment组和Control组样本不一致时，其表达的增量存在偏差。因此对上式做一个缩放修改，相当于以Treatment组的样本量为准，对Control组做一个缩放，累积绘制的曲线称为Qini 曲线。

另外一种相似的Qini Curve表示如下，将Qini系数定义为曲线下的面积

另外，取Qini曲线下面积为Qini系数。

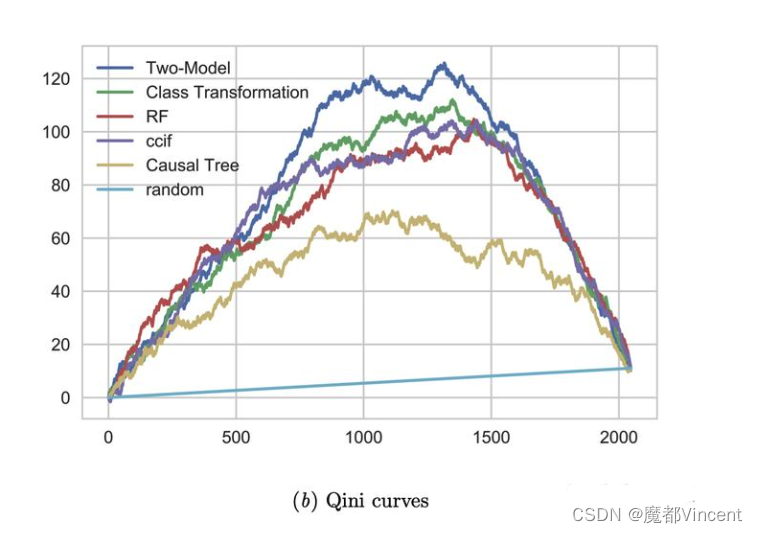
可以看到qini curve与uplift curve的关系如下（平衡情况下系数为2）：

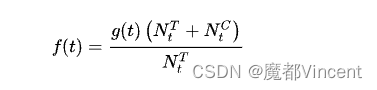
通常情况下，Uplift Curve会受实验对照组样本数比例影响，Qini Curve更稳定一些。

Qini系数相对AUUC的好处：

1. Qini系数做了T组和C组的样本缩放，解决AUUC在T组比C组多很多时不适用的问题；
2. Qini系数是归一化后的，这样它就可以在不同的数据集间做一个对比。

最后，我们总结一下Uplift模型可能的应用场景：

• 精准定位策略敏感人群：如全文所述，我们希望找出来一些对干预项（例如发券、投放等）比较敏感的用户，继而对其进行精准策略/营销；
• 测算收益空间：Uplift模型可以帮助我们测算如果对策略做一些人群向优化，业务收益将会提升多少；

大白话谈因果系列文章（三）估计uplift--传统统计学习方法 - 知乎 (zhihu.com)

增益模型（Uplift Model）的基础介绍 —— 估算ITE - 知乎 (zhihu.com)该把优惠券发送给哪些用户？一文读懂Uplift模型 - 知乎 (zhihu.com)

大白话谈因果系列文章（五）uplift模型评估 - 知乎 (zhihu.com)

【Uplift】建模方法篇 - 知乎 (zhihu.com)

【Uplift】评估方法篇 - 知乎 (zhihu.com)

智能营销与因果推断-uplift模型 - 知乎 (zhihu.com)

Uplift-Model - 知乎 (zhihu.com)

Uplift Modeling的相关案例介绍 - 知乎 (zhihu.com)