1、高斯混合模型概述
高斯混合模型 (GMM) 是一种机器学习算法。它们用于根据概率分布将数据分类为不同的类别。高斯混合模型可用于许多不同的领域,包括金融、营销等等!这里要对高斯混合模型进行介绍以及真实世界的示例、它们的作用以及何时应该使用GMM。
高斯混合模型 (GMM) 是一个概率概念,用于对真实世界的数据集进行建模。GMM是高斯分布的泛化,可用于表示可聚类为多个高斯分布的任何数据集。
高斯混合模型是一种概率模型,它假设所有数据点都是从具有未知参数的高斯分布的混合中生成的。
高斯混合模型可用于聚类,这是将一组数据点分组为聚类的任务。GMM 可用于在数据集中可能没有明确定义的集群中查找集群。此外,GMM 可用于估计新数据点属于每个集群的概率。高斯混合模型对异常值也相对稳健,这意味着即使有一些数据点不能完全适合任何集群,它们仍然可以产生准确的结果。这使得 GMM 成为一种灵活而强大的数据聚类工具。它可以被理解为一个概率模型,其中为每个组假设高斯分布,并且它们具有定义其参数的均值和协方差。
GMM 由两部分组成——均值向量 (μ) 和协方差矩阵 (Σ)。高斯分布被定义为呈钟形曲线的连续概率分布。高斯分布的另一个名称是正态分布。这是高斯混合模型的图片:它可以被理解为一个概率模型,其中为每个组假设高斯分布,并且它们具有定义其参数的均值和协方差。GMM 由两部分组成——均值向量 (μ) 和协方差矩阵 (Σ)。高斯分布被定义为呈钟形曲线的连续概率分布。高斯分布的另一个名称是正态分布。这是高斯混合模型的图片:
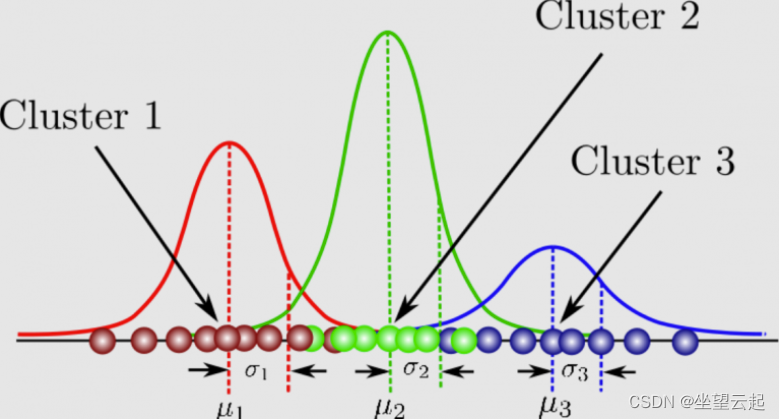
GMM 有许多应用,例如密度估计、聚类和图像分割。对于密度估计,GMM 可用于估计一组数据点的概率密度函数。对于聚类,GMM 可用于将来自相同高斯分布的数据点组合在一起。对于图像分割,GMM 可用于将图像划分为不同的区域。
高斯混合模型可用于各种用例,包括识别客户群、检测欺诈活动和聚类图像。在这些示例中的每一个中,高斯混合模型都能够识别数据中可能不会立即明显的聚类。因此,高斯混合模型是一种强大的数据分析工具,应该考虑用于任何聚类任务。
在高斯混合模型中,期望最大化方法是估计高斯混合模型(GMM)参数的有力工具。期望称为E,最大化称为M。期望用于找到用于表示高斯混合模型的每个分量的高斯参数。最大化被称为 M 并且它涉及确定是否可以添加新数据点,可以从下面链接进一步了解期望最大化。
Opencv学习笔记 - 使用opencvsharp和期望最大化_坐望云起的博客-CSDN博客期望最大化的受欢迎程度在很大程度上是因为它是从观察中学习参数的有效且稳健的程序。然而,通常可用于训练概率模型的唯一数据是不完整的。例如,在医学诊断中可能会出现缺失值,其中患者病史通常包括有限的一组测试的结果。或者,在基因表达聚类中,数据不完整源于在概率模型中有意省略基因到簇的分配。期望最大化算法能够在数据不完整的概率模型中进行参数估计。期望最大化算法(Expectation Maximization),是一种渐进逼近算法,通过迭代进行极大似然估计的优化算法。https://skydance.blog.csdn.net/article/details/122015022 在这里,我们将探索高斯混合模型,这是一种无监督的聚类和密度估计技术。
2、高斯混合模型数学原理
高斯混合模型是指具有如下形式的概率分布模型,
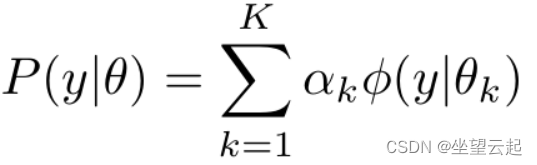
其中,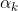是系数,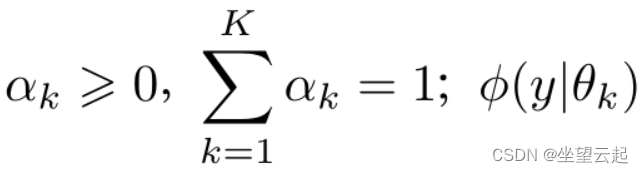是高斯分布密度,。
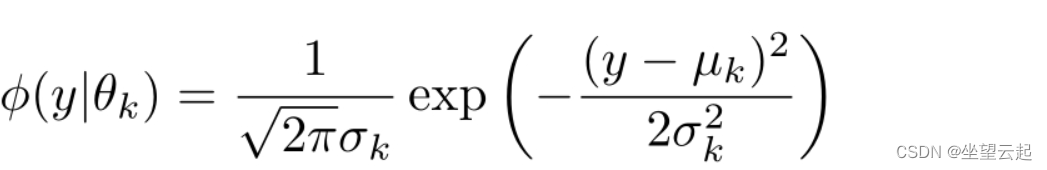称为第k个分模型。
一般混合模型可以由任意概率分布密度代替式中的高斯分布密度,我们只介绍最常用的高斯混合模型。
3、使用高斯混合模型步骤
以下是使用高斯混合模型的三个不同步骤:
确定定义每个高斯如何相互关联的协方差矩阵。两个高斯分布越相似,它们的均值就越接近,反之亦然,如果它们在相似性方面彼此相距很远。高斯混合模型可以具有对角线或对称的协方差矩阵。
确定每组中的高斯数定义了有多少簇。
选择定义如何使用高斯混合模型优化分离数据的超参数,以及决定每个高斯的协方差矩阵是对角线还是对称的。
4、与其他聚类算法的区别
以下是高斯混合模型和用于聚类的 K-means 算法之间的一些主要区别:
高斯混合模型是一种聚类算法,它假设数据点是由具有未知参数的高斯分布的混合生成的。该算法的目标是估计高斯分布的参数,以及来自每个分布的数据点的比例。相比之下,K-means 是一种聚类算法,它不对数据点的潜在分布做出任何假设。相反,它只是将数据点划分为 K 个集群,其中每个集群由其质心定义。
虽然高斯混合模型更灵活,但它们可能比 K-means 更难训练。K-means 通常收敛速度更快,因此在运行时是一个重要考虑因素的情况下可能是首选。
一般来说,当数据集较大且聚类分离良好时,K-means 会更快、更准确。当数据集较小或聚类分离不充分时,高斯混合模型会更准确。
高斯混合模型考虑了数据的方差,而 K-means 没有。
高斯混合模型在簇的形状方面更加灵活,而 K-means 仅限于球形簇。
高斯混合模型可以处理缺失数据,而 K-means 不能。这种差异可以使高斯混合模型在某些应用中更有效,例如具有大量噪声的数据或未明确定义的数据。
5、适合的应用场景
高斯混合模型可用于各种场景,包括当数据由混合高斯分布生成时,当集群的正确数量存在不确定性时,以及当集群具有不同的形状时。在每种情况下,使用高斯混合模型都有助于提高结果的准确性。例如,当数据是由混合高斯分布生成时,使用高斯混合模型可以帮助更好地识别数据中的潜在模式。此外,当对正确的聚类数量存在不确定性时,使用高斯混合模型可以帮助降低错误率。
高斯混合模型可用于异常检测;通过将模型拟合到数据集然后对新数据点进行评分,可以标记与其余数据显着不同的点(即异常值)。这对于识别欺诈或检测数据收集中的错误很有用。
在时间序列分析的情况下,GMM 可用于发现波动性与趋势和噪声之间的关系,这有助于预测未来的股票价格。一个集群可能包含时间序列中的趋势,而另一个集群可能包含来自其他因素的噪音和波动,例如影响股价的季节性或外部事件。为了分离出这些集群,可以使用 GMM,因为它们为每个类别提供概率,而不是像 K-means 那样简单地将数据分成两部分。
另一个例子是当数据集中有不同的组并且很难将它们标记为属于一个或另一个组时,这使得其他机器学习算法(例如 K-means 聚类算法)难以分离数据。在这种情况下可以使用 GMM,因为它们找到了最能描述每个组的高斯混合模型,并为每个集群提供了一个概率,这在标记集群时很有帮助。
高斯混合模型可以生成与原始数据相似的合成数据点,也可以用于数据增强。
6、实际应用介绍
以下是一些可以使用高斯混合模型解决的实际问题:
在医疗数据集中寻找模式:GMM 可用于根据图像内容将图像分割成多个类别,或在医疗数据集中寻找特定模式。它们可用于查找具有相似症状的患者群、识别疾病亚型,甚至预测结果。在最近的一项研究中,使用高斯混合模型来分析超过 700,000 条患者记录的数据集。该模型能够识别数据中以前未知的模式,这可能会为癌症患者带来更好的治疗。
对自然现象建模:GMM 可用于对发现噪声遵循高斯分布的自然现象进行建模。这种概率建模模型依赖于以下假设,即存在一些潜在的未观察实体或属性的连续体,并且每个成员都与在多个观察会话中等距点进行的测量相关联。
客户行为分析:GMM 可用于在营销中执行客户行为分析,以根据历史数据预测未来的购买情况。
股票价格预测:使用高斯混合模型的另一个领域是金融领域,它们可以应用于股票的价格时间序列。GMM 可用于检测时间序列数据中的变化点,并帮助找到由于波动性和噪声而难以发现的股票价格或其他市场走势的转折点。
基因表达数据分析:高斯混合模型可用于基因表达数据分析。特别是,GMM 可用于检测两种情况之间的差异表达基因,并确定哪些基因可能有助于某种表型或疾病状态。
7、基于GMM的异常点检测
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.mixture import GaussianMixture as GMM
plt.style.use('seaborn')
# 特定分布的一维数据
np.random.seed(2)
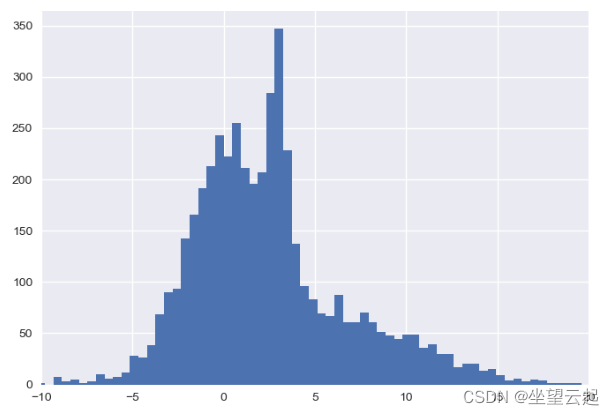
x = np.concatenate([np.random.normal(0, 2, 2000), np.random.normal(5, 5, 2000), np.random.normal(3, 0.5, 600)])
plt.hist(x, 80)
plt.xlim(-10, 20);
plt.show()
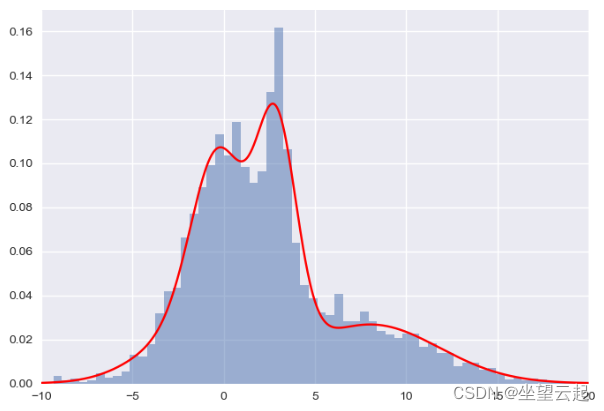
# 高斯混合模型将允许我们近似这个密度:
X = x[:, np.newaxis]
clf = GMM(4, max_iter=500, random_state=3).fit(X)
xpdf = np.linspace(-10, 20, 1000)
density = np.array([np.exp(clf.score([[xp]])) for xp in xpdf])
plt.hist(x, 80, density=True, alpha=0.5)
plt.plot(xpdf, density, '-r')
plt.xlim(-10, 20)
plt.show()
plt.hist(x, 80, alpha=0.3)
plt.plot(xpdf, density, '-r')
for i in range(clf.n_components):
pdf = clf.weights_[i] * stats.norm(clf.means_[i, 0], np.sqrt(clf.covariances_[i, 0])).pdf(xpdf)
plt.fill(xpdf, pdf, facecolor='gray', edgecolor='none', alpha=0.3)
plt.xlim(-10, 20)
plt.show()
np.random.seed(0)
# Add 20 outliers
true_outliers = np.sort(np.random.randint(0, len(x), 20))
y = x.copy()
y[true_outliers] += 50 * np.random.randn(20)
clf = GMM(4, max_iter=500, random_state=0).fit(y[:, np.newaxis])
xpdf = np.linspace(-10, 20, 1000)
density_noise = np.array([np.exp(clf.score([[xp]])) for xp in xpdf])
plt.hist(y, 80, density=True, alpha=0.5)
plt.plot(xpdf, density_noise, '-r')
plt.xlim(-15, 30);
plt.show()
log_likelihood = np.array([clf.score_samples([[yy]]) for yy in y])
# log_likelihood = clf.score_samples(y[:, np.newaxis])[0]
plt.plot(y, log_likelihood, '.k');
plt.show()
detected_outliers = np.where(log_likelihood < -9)[0]
print("true outliers:")
print(true_outliers)
print("\ndetected outliers:")
print(detected_outliers)
版权归原作者 坐望云起 所有, 如有侵权,请联系我们删除。