MPC（模型预测控制）控制小车沿轨迹移动——C++实现

任务说明

要求如下图所示，给定一条轨迹，要求控制小车沿这条轨迹移动，同时可以适用于系统带有延时的情况。注意，本篇文章只给出部分C++代码参考。

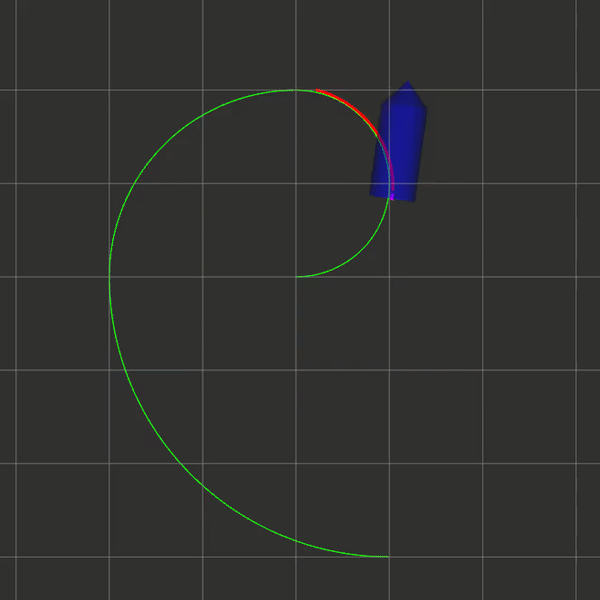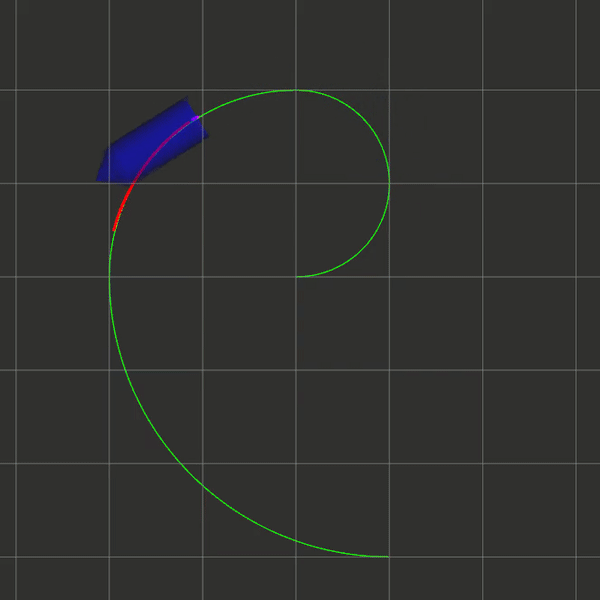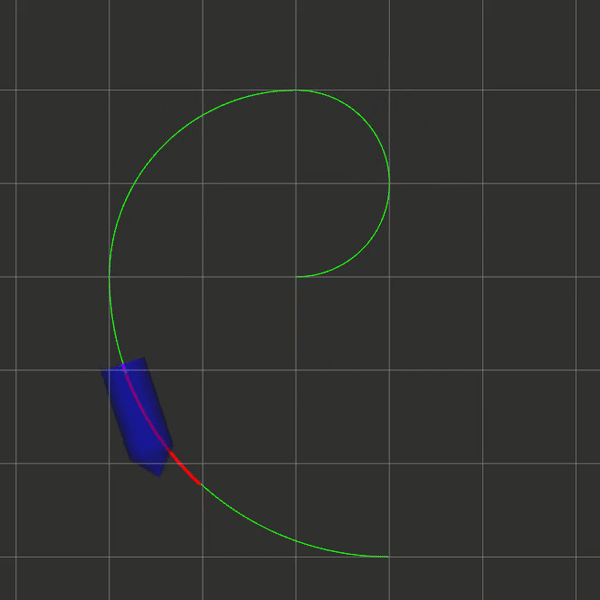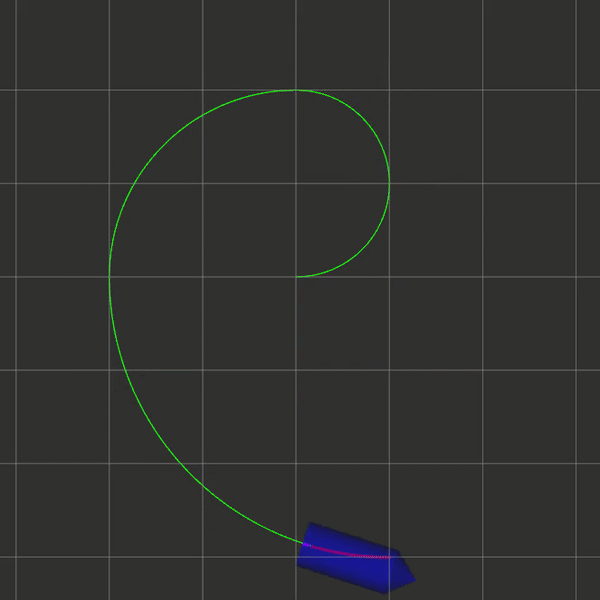
主要流程

首先用运动学自行车模型（Kinematic Bicycle Model）对小车建模，设计相应的成本函数（cost function）和约束，之后利用OSQP求解二次规划问题，实现线性时变模型预测控制（Linear Time-Varying MPC）器。

运动学自行车模型（Kinematic Bicycle Model）

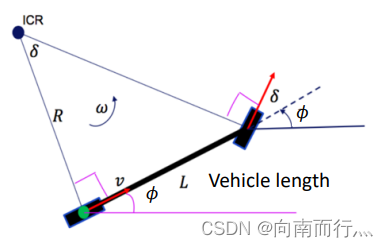
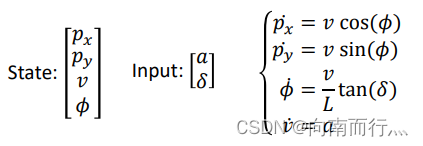
首先我们来讲一下运动学自行车模型，如下图所示，小车的运动学模型可以当作是一个自行车，前轮控制拐的角度 $\delta$ ，后轮控制加速度 $a$ ，所以这两个量就是我们就控制量。系统的状态为惯性系中小车后轮的 $x$ 和 $y$ 的坐标，惯性系速度 $v$ 以及小车相对于惯性系的姿态角 $\phi$ ，其微分的形式如下式所示：

线性时变模型预测控制（Linear Time-Varying MPC）

动力学系统模型

一个普通动力学系统的模型如下图所示，首先其状态量可以微分，其微分形式是关于系统状态和控制量的一个函数。其次系统的下一个状态也是相当于当前状态与当前状态采取的控制量相关的一个函数。

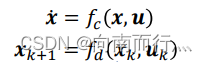
线性模型

如果一个动力学系统是线性的，那么就可以写成以下的形式，其中 $A$ 和 $B$ 是系数，如果不是时变模型的话，其值不会改变：

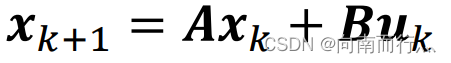
那么我们就可以将其推导成与初始状态 $x_0$ 相关的形式：

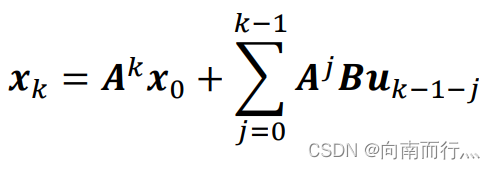
那么其矩阵形式就是这样的：

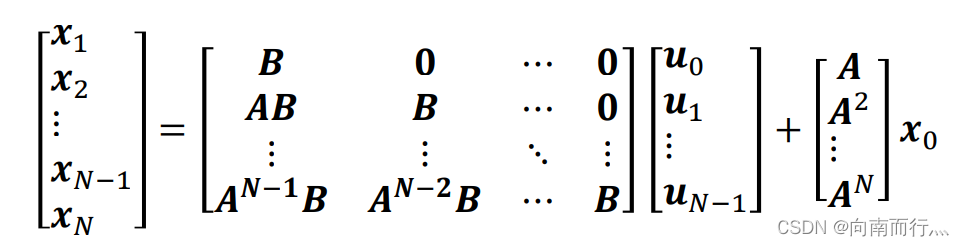
线性时变模型

线性时变模型就是系统的系数 $A$ 和 $B$ 会随时间 $t$ 改变：

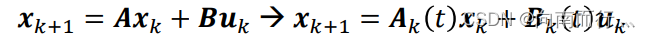
我们重看回运动学自行车模型，发现其系统模型并不是线性的（因为系统模型中存在三角函数），那么我们可以将其线性化，通过以下的形式，我们就可以将非线性模型转换成线性时变模型，其中上面带横线的变量是参考系统的状态和输出，也就是我们希望的状态量和输出量，比如说，我们希望系统的位置处于轨迹点上，并且速度为期望值。

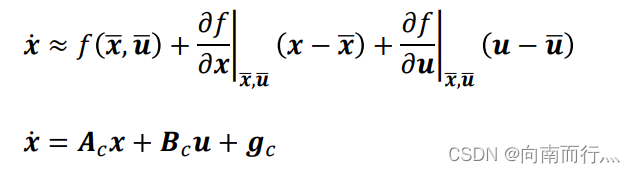
我们会发现，相比于线性模型，会多出一个系数 $g$ ，下面我们来通过线性化运动学自行车模型来看是不是会多出这一项。

线性化模型（Model linearization）

我们利用上面线性化的公式对运动学自行车模型进行线性化：

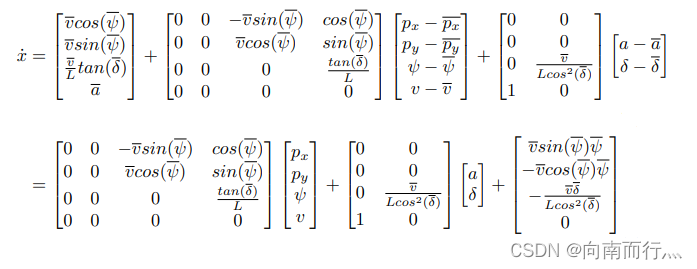
那么就得到：

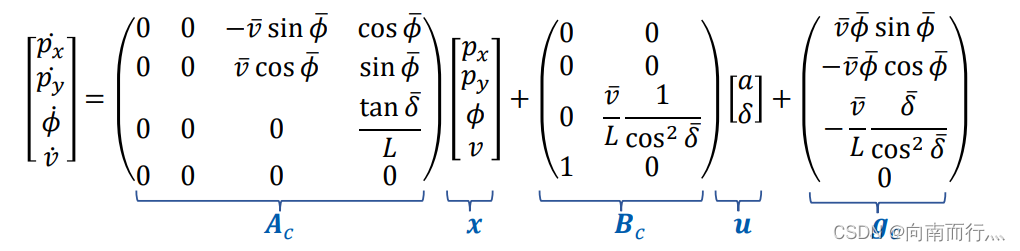
我们将其离散化，方便求解和控制：

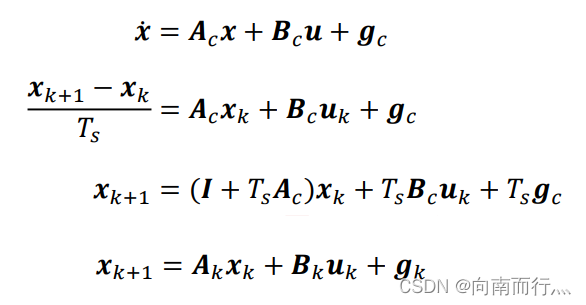
其线性化模型的C++的代码如下，其中 ll_就是公式中的 $L$ ，dt_ 就是时间 $T_s$ ：

static constexpr int n = 4;  // state x y phi v
static constexpr int m = 2;  // input a delta
typedef Eigen::Matrix<double, n, n> MatrixA;
typedef Eigen::Matrix<double, n, m> MatrixB;
typedef Eigen::Vector4d VectorG;
typedef Eigen::Vector4d VectorX;
typedef Eigen::Vector2d VectorU;

void linearization(const double &phi, const double &v, const double &delta) {
    Ad_ <<  0, 0, -v*sin(phi), cos(phi),
            0, 0,  v*cos(phi), sin(phi),
            0, 0, 0, tan(delta) / ll_,
            0, 0, 0, 0;
    Bd_ <<  0, 0,
            0, 0,
            0, v/(ll_*pow(cos(delta),2)),
            1, 0;
    gd_ <<  v*phi*sin(phi), -v*phi*cos(phi), -v*delta/(ll_*pow(cos(delta),2)), 0;

    Ad_ = MatrixA::Identity() + dt_ * Ad_;
    Bd_ = dt_ * Bd_;
    gd_ = dt_ * gd_;
    return;
  }

设计成本函数（cost function）和约束

设计成本函数

我们要得到一个最优的控制量，那么就要有一个目标，这个目标要求整个系统从起始状态到终止状态的总成本最小，其可以分成两个部分，其中一个是表示系统状态转移时的成本，由当前状态和当前控制共同决定，另一个是系统到终止状态时花费的成本，两者相加就是总成本：

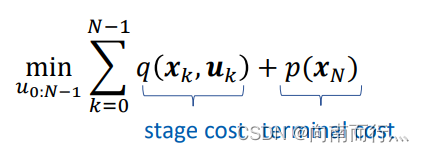
同时系统要满足系统状态转换的约束和一些等式约束和不等式约束：

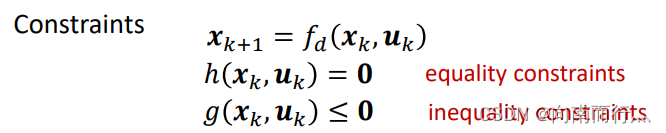
在本次小车跟踪轨迹的任务中我们设计的成本函数是这样的，要求小车在当前位置与轨迹的位置误差和偏航角误差尽量小：

$\large J=(x-x_{ref})^2+(y-y_{ref})^2+\rho (\phi-\phi_{ref})^2$

那么我们就可以设计一个 Q 矩阵，其中每一个小方括号代表每一个系统状态，每一行对应 $x$ 和 $y$ 的坐标，小车姿态角 $\phi$ 以及速度 $v$ ，如果我们设置预测步长为40个，那么就有40个小方括号，其中 $\rho _N$ 表示最终状态的系数，由于系统的stage cost和terminal cost不一样所以设置得不一样，一般我们认为最终状态速度要为 0，所以最后一个元素就设置成 1：

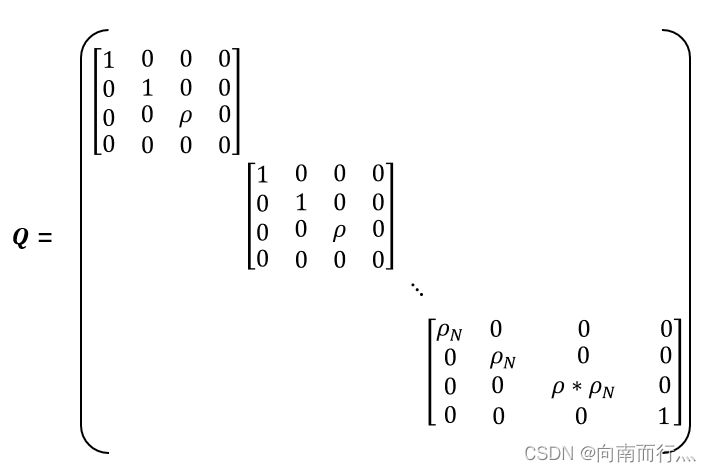
那么系统的成本函数就可以写成如下形式，注意这里的 $\large \textbf{x}$ 是一个向量，表示系统的状态：

$\large J=(\textbf{x}-\textbf{x}_{ref})^T\textbf{Q}(\textbf{x}-\textbf{x}_{ref})$

约束

这里我们设置的约束比较简单，就只是一些不等式约束：

$\large -v_{max}\leqslant v\leqslant v_{max}$

$\large -a_{max}\leqslant a\leqslant a_{max}$

$\large -\delta_{max}\leqslant \delta\leqslant \delta _{max}$

$\large -\dot{\delta}_{max} * \Delta t\leqslant \dot{\delta}\leqslant \dot{\delta}_{max} * \Delta t$

由于我们要输入到OSQP上，所以要对这些变量作一些处理，其C++代码如下，其中N_代表MPC的预测步长：

/* *
   *               /  x1  \
   *               |  x2  |
   *  lx_ <=  Cx_  |  x3  |  <= ux_
   *               | ...  |
   *               \  xN  /
   * */
  Eigen::SparseMatrix<double> Cx_, lx_, ux_;  // p, v constrains
  /* *
   *               /  u0  \
   *               |  u1  |
   *  lu_ <=  Cu_  |  u2  |  <= uu_
   *               | ...  |
   *               \ uN-1 /
   * */
  Eigen::SparseMatrix<double> Cu_, lu_, uu_;  // a delta vs constrains
  Eigen::SparseMatrix<double> Qx_;

// set size of sparse matrices
    P_.resize(m * N_, m * N_);
    q_.resize(m * N_, 1);
    Qx_.resize(n * N_, n * N_);
    // stage cost
    Qx_.setIdentity();
    for (int i = 1; i < N_; ++i) {
      Qx_.coeffRef(i * n - 2, i * n - 2) = rho_;
      Qx_.coeffRef(i * n - 1, i * n - 1) = 0;
    }
    Qx_.coeffRef(N_ * n - 4, N_ * n - 4) = rhoN_;
    Qx_.coeffRef(N_ * n - 3, N_ * n - 3) = rhoN_;
    Qx_.coeffRef(N_ * n - 2, N_ * n - 2) = rhoN_ * rho_;
    int n_cons = 4;  // v a delta ddelta
    A_.resize(n_cons * N_, m * N_);
    l_.resize(n_cons * N_, 1);
    u_.resize(n_cons * N_, 1);
    // v constrains
    Cx_.resize(1 * N_, n * N_);
    lx_.resize(1 * N_, 1);
    ux_.resize(1 * N_, 1);
    // a delta constrains
    Cu_.resize(3 * N_, m * N_);
    lu_.resize(3 * N_, 1);
    uu_.resize(3 * N_, 1);
    // set lower and upper boundaries
    for (int i = 0; i < N_; ++i) {
      // -a_max <= a <= a_max for instance:
      Cu_.coeffRef(i * 3 + 0, i * m + 0) = 1;
      lu_.coeffRef(i * 3 + 0, 0) = -a_max_;
      uu_.coeffRef(i * 3 + 0, 0) = a_max_;
      // ...
      Cu_.coeffRef(i * 3 + 1, i * m + 1) = 1;
      lu_.coeffRef(i * 3 + 1, 0) = -delta_max_;
      uu_.coeffRef(i * 3 + 1, 0) = delta_max_;

      Cu_.coeffRef(i * 3 + 2, i * m + 1) = 1;
      if (i > 0){
        Cu_.coeffRef(i * 3 + 2, (i - 1) * m + 1) = -1;
      }
      lu_.coeffRef(i * 3 + 2, 0) = -ddelta_max_ * dt_;
      uu_.coeffRef(i * 3 + 2, 0) = ddelta_max_ * dt_;

      // -v_max <= v <= v_max
      Cx_.coeffRef(i, i * n + 3) = 1;
      lx_.coeffRef(i, 0) = -v_max_;
      ux_.coeffRef(i, 0) = v_max_;
    }

求解二次规划问题

这样，我们就可以通过得到系统的当前状态 $\textbf{x}_0$ ，然后通过下式得到未来预测 $N$ 步的状态，注意下式中的 $A$ 和 $B$ 此时已经不再是一样的，都是随时间而不同（也就是说其实是有下标的），因为现在是线性时变模型：

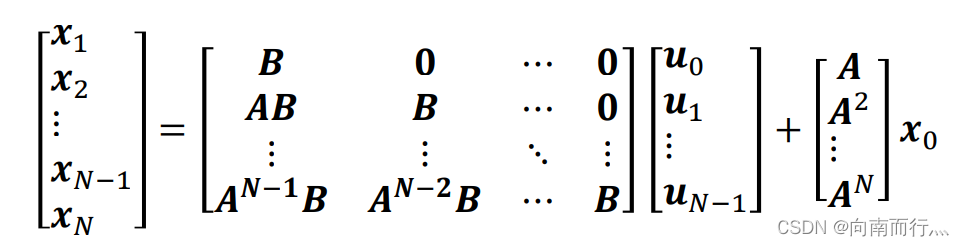
这个才是正确的，在下面的代码中就是AA BB gg矩阵的构建：

之后我们就可以将我们要求解的问题根据OSQP的需要一步步处理完输进去。

具体怎么用OSQP求解可以参考下面这个链接，输入到OSQP的形式是什么样子的都可以看到：

使用OSQP解决二次凸优化(QP)问题

首先是cost function，我们先推导出其形式：

$\large J=(\textbf{x}-\textbf{x}_{ref})^T\textbf{Q}(\textbf{x}-\textbf{x}_{ref})$

这里为了表达方便，我们就作如下简化，分别用这几个变量代替：

将下式代入到上式：

$\large \textbf{x}=\textbf{A}\textbf{x}_0 + \textbf{B}\textbf{u}+\textbf{g}=\bar{\textbf{T}}\textbf{x}_0 + \bar{\textbf{S}}\textbf{Z}+\textbf{g}$

由于自变量是控制量 $\textbf{Z}$ ，我们可以在推导的过程把没有 $\textbf{Z}$ 的项直接去掉，推导的过程我就不一一写出来了，最后我们就可以得到：

$\large J=\frac{1}{2}\textbf{Z}^T\bar{\textbf{S}}^T\textbf{Q}\bar{\textbf{S}}\textbf{Z}+[(\bar{\textbf{T}}\textbf{x}_0+\textbf{g})^T\textbf{Q}\bar{\textbf{S}}-{\textbf{x}_{ref}}^T\textbf{Q}\bar{\textbf{S}}]\textbf{Z}$

那么输入到OSQP的前两个矩阵就是：

$\large H = \bar{\textbf{S}}^T\textbf{Q}\textbf{S} \ \ \ \ f= \textbf{S}\bar{\textbf{Q}}^T (\bar{\textbf{T}}\textbf{x}_0+\textbf{g})+\textbf{S}\textbf{q}_x$

其中：

$\large \textbf{q}_x = -\textbf{Q}^T\textbf{x}_{ref}$

之后我们把对应的上界约束和下界约束转换成与控制量有关的形式，输入进OSQP中，就能得出我们的最优控制量。下面就是相关的代码：

int solveQP(const VectorX& x0_observe) {
    x0_observe_ = x0_observe;
    historyInput_.pop_front();
    historyInput_.push_back(predictInput_.front());
    lu_.coeffRef(2, 0) = predictInput_.front()(1) - ddelta_max_ * dt_;
    uu_.coeffRef(2, 0) = predictInput_.front()(1) + ddelta_max_ * dt_;
    VectorX x0 = compensateDelay(x0_observe_);
    // set BB, AA, gg
    Eigen::MatrixXd BB, AA, gg;
    BB.setZero(n * N_, m * N_);
    AA.setZero(n * N_, n);
    gg.setZero(n * N_, 1);
    double s0 = s_.findS(x0.head(2));
    double phi, v, delta;
    double last_phi = x0(2);
    Eigen::SparseMatrix<double> qx;
    qx.resize(n * N_, 1);
    for (int i = 0; i < N_; ++i) {
      calLinPoint(s0, phi, v, delta);
      if (phi - last_phi > M_PI) {
          phi -= 2 * M_PI;
      } else if (phi - last_phi < -M_PI) {
          phi += 2 * M_PI;
      }
      last_phi = phi;
      linearization(phi, v, delta);
      // calculate big state-space matrices
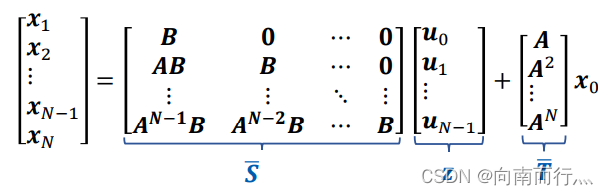
      /* *                BB                AA
       * x1    /       B    0  ... 0 \    /   A \
       * x2    |      AB    B  ... 0 |    |  A2 |
       * x3  = |    A^2B   AB  ... 0 |u + | ... |x0 + gg
       * ...   |     ...  ...  ... 0 |    | ... |
       * xN    \A^(n-1)B  ...  ... B /    \ A^N /
       *
       *     X = BB * U + AA * x0 + gg
       * */
      if (i == 0) {
        BB.block(0, 0, n, m) = Bd_;
        AA.block(0, 0, n, n) = Ad_;
        gg.block(0, 0, n, 1) = gd_;
      } else {
        BB.block(i * n, i * m, n, m) = Bd_;
        for (int j = i - 1; j >= 0; --j){
          BB.block(i * n, j * m, n, m) = Ad_ * BB.block((i - 1) * n, j * m, n, m);
        }
        AA.block(i * n, 0, n, n) = Ad_ * AA.block((i - 1) * n, 0, n, n);
        gg.block(i * n, 0, n, 1) = Ad_ * gg.block((i - 1) * n, 0, n, 1) + gd_;
      }
      Eigen::Vector2d xy = s_(s0);  // reference (x_r, y_r)

      // cost function should be represented as follows:
      /* *
       *           /  x1  \T       /  x1  \         /  x1  \
       *           |  x2  |        |  x2  |         |  x2  |
       *  J =  0.5 |  x3  |   Qx_  |  x3  | + qx^T  |  x3  | + const.
       *           | ...  |        | ...  |         | ...  |
       *           \  xN  /        \  xN  /         \  xN  /
       * */

      qx.coeffRef(i * n + 0, 0) = -Qx_.coeffRef(i * n + 0, i * n + 0) * xy(0);
      qx.coeffRef(i * n + 1, 0) = -Qx_.coeffRef(i * n + 1, i * n + 1) * xy(1);
      qx.coeffRef(i * n + 2, 0) = -Qx_.coeffRef(i * n + 2, i * n + 2) * phi;
      qx.coeffRef(i * n + 3, 0) = -Qx_.coeffRef(i * n + 3, i * n + 3) * v;

      s0 += desired_v_ * dt_;
      s0 = s0 < s_.arcL() ? s0 : s_.arcL();
    }
    Eigen::SparseMatrix<double> BB_sparse = BB.sparseView();
    Eigen::SparseMatrix<double> AA_sparse = AA.sparseView();
    Eigen::SparseMatrix<double> gg_sparse = gg.sparseView();
    Eigen::SparseMatrix<double> x0_sparse = x0.sparseView();

    // state constrants propogate to input constraints using "X = BB * U + AA * x0 + gg"
    /* *
     *               /  x1  \                              /  u0  \
     *               |  x2  |                              |  u1  |
     *  lx_ <=  Cx_  |  x3  |  <= ux_    ==>    lx <=  Cx  |  u2  |  <= ux
     *               | ...  |                              | ...  |
     *               \  xN  /                              \ uN-1 /
     * */
    Eigen::SparseMatrix<double> Cx = Cx_ * BB_sparse;
    Eigen::SparseMatrix<double> lx = lx_ - Cx_ * AA_sparse * x0_sparse - Cx_ * gg_sparse;
    Eigen::SparseMatrix<double> ux = ux_ - Cx_ * AA_sparse * x0_sparse - Cx_ * gg_sparse;

    /* *      / Cx  \       / lx  \       / ux  \
     *   A_ = \ Cu_ /, l_ = \ lu_ /, u_ = \ uu_ /
     * */

    Eigen::SparseMatrix<double> A_T = A_.transpose();
    A_T.middleCols(0, Cx.rows()) = Cx.transpose();
    A_T.middleCols(Cx.rows(), Cu_.rows()) = Cu_.transpose();
    A_ = A_T.transpose();
    for (int i = 0; i < lx.rows(); ++i) {
      l_.coeffRef(i, 0) = lx.coeff(i, 0);
      u_.coeffRef(i, 0) = ux.coeff(i, 0);
    }
    for (int i = 0; i < lu_.rows(); ++i) {
      l_.coeffRef(i + lx.rows(), 0) = lu_.coeff(i, 0);
      u_.coeffRef(i + lx.rows(), 0) = uu_.coeff(i, 0);
    }
    Eigen::SparseMatrix<double> BBT_sparse = BB_sparse.transpose();
    P_ = BBT_sparse * Qx_ * BB_sparse;
    q_ = BBT_sparse * Qx_.transpose() * (AA_sparse * x0_sparse + gg_sparse) + BBT_sparse * qx;
    // osqp
    Eigen::VectorXd q_d = q_.toDense();
    Eigen::VectorXd l_d = l_.toDense();
    Eigen::VectorXd u_d = u_.toDense();
    qpSolver_.setMats(P_, q_d, A_, l_d, u_d);
    qpSolver_.solve();
    int ret = qpSolver_.getStatus();
    if (ret != 1) {
      ROS_ERROR("fail to solve QP!");
      return ret;
    }
    solve_flag = true;
    Eigen::VectorXd sol = qpSolver_.getPrimalSol();
    Eigen::MatrixXd solMat = Eigen::Map<const Eigen::MatrixXd>(sol.data(), m, N_);
    Eigen::VectorXd solState = BB * sol + AA * x0 + gg;
    Eigen::MatrixXd predictMat = Eigen::Map<const Eigen::MatrixXd>(solState.data(), n, N_);

    for (int i = 0; i < N_; ++i) {
      predictInput_[i] = solMat.col(i);
      predictState_[i] = predictMat.col(i);
    }
    return ret;
  }

延时模型

注意到上面的代码中有：

VectorX x0 = compensateDelay(x0_observe_);

这个函数就是要考虑延时的情况，当系统是无延时的时候状态就是它本身。

延时模型的意思就是系统当前的控制量并不会马上作用于当前的系统，而是会经过一段时间 $\tau$ 后才作用，也就是说系统的控制是有延时的，如下所示：

那么我们就可以把系统的初始状态 $\textbf{x}_0$ 定义成当前时刻 $\tau$ 之后的状态量，由于我们用的是MPC，可以预测当前时刻 $\tau$ 之后的状态，那么我们就可以利用类似之前AA BB gg矩阵的形式来得到一个delay后的状态，然后我们就可以利用这个状态得到相应的延时控制量，如下所示：

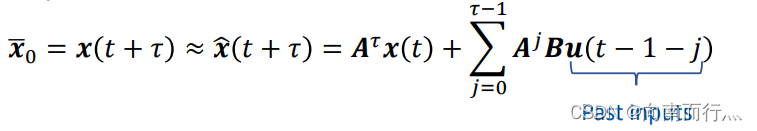
其代码如下：

  VectorX compensateDelay(const VectorX& x0) {
    VectorX x0_delay = x0;
    if (delay_ == 0)
    {
      return x0_delay;
    }
    Eigen::MatrixXd BB, AA, gg, x0_pred;
    int tau = std::ceil(delay_ / dt_);
    BB.setZero(n * tau, m * tau);
    AA.setZero(n * tau, n);
    gg.setZero(n * tau, 1);
    x0_pred.setZero(n * tau, 1);
    double s0 = s_.findS(x0.head(2));
    double phi, v, delta;
    double last_phi = x0(2);

    for (int i = 0; i < tau; ++i) {
      calLinPoint(s0, phi, v, delta);
      if (phi - last_phi > M_PI) {
        phi -= 2 * M_PI;
      } else if (phi - last_phi < -M_PI) {
        phi += 2 * M_PI;
      }
      last_phi = phi;
      linearization(phi, v, delta);
      if (i == 0) {
          BB.block(0, 0, n, m) = Bd_;
          AA.block(0, 0, n, n) = Ad_;
          gg.block(0, 0, n, 1) = gd_;
        } else {
          BB.block(i * n, i * m, n, m) = Bd_;
          for (int j = i - 1; j >= 0; --j){
            BB.block(i * n, j * m, n, m) = Ad_ * BB.block((i - 1) * n, j * m, n, m);
          }
          AA.block(i * n, 0, n, n) = Ad_ * AA.block((i - 1) * n, 0, n, n);
          gg.block(i * n, 0, n, 1) = Ad_ * gg.block((i - 1) * n, 0, n, 1) + gd_;
        }
      }
    Eigen::VectorXd uu(m * tau, 1);
    for (double t = delay_; t > 0; t -= dt_) {
      int i = std::ceil(t / dt_);
      uu.coeffRef((tau - i) * m + 0, 0) = historyInput_[i - 1][0];
      uu.coeffRef((tau - i) * m + 1, 0) = historyInput_[i - 1][1];
    }
    x0_pred = BB * uu + AA * x0 + gg;
    x0_delay = x0_pred.block((tau - 1) * n, 0, n, 1);
    return x0_delay;
  }

效果图（注意看小车末尾的紫色线条表示延时）：

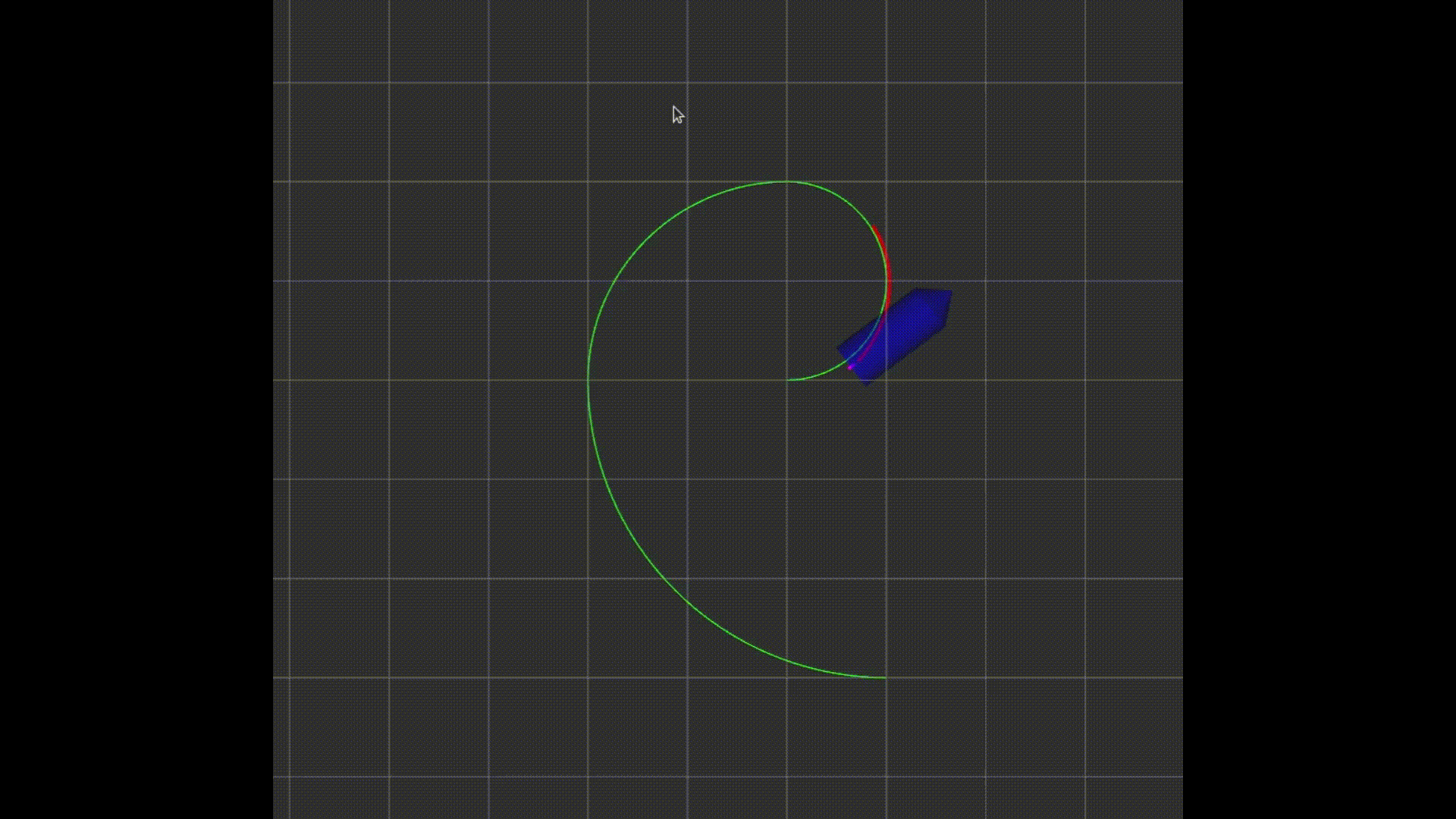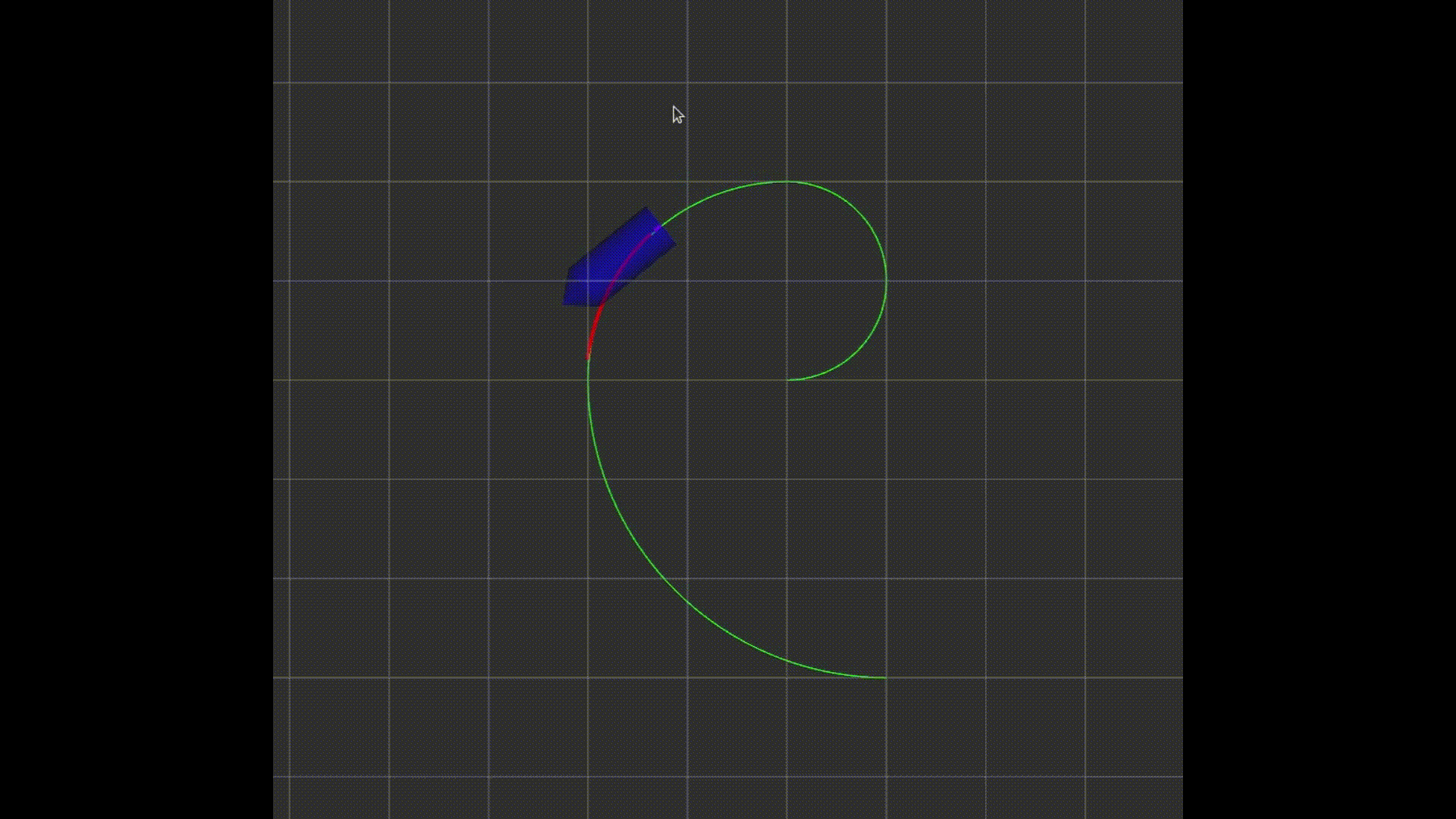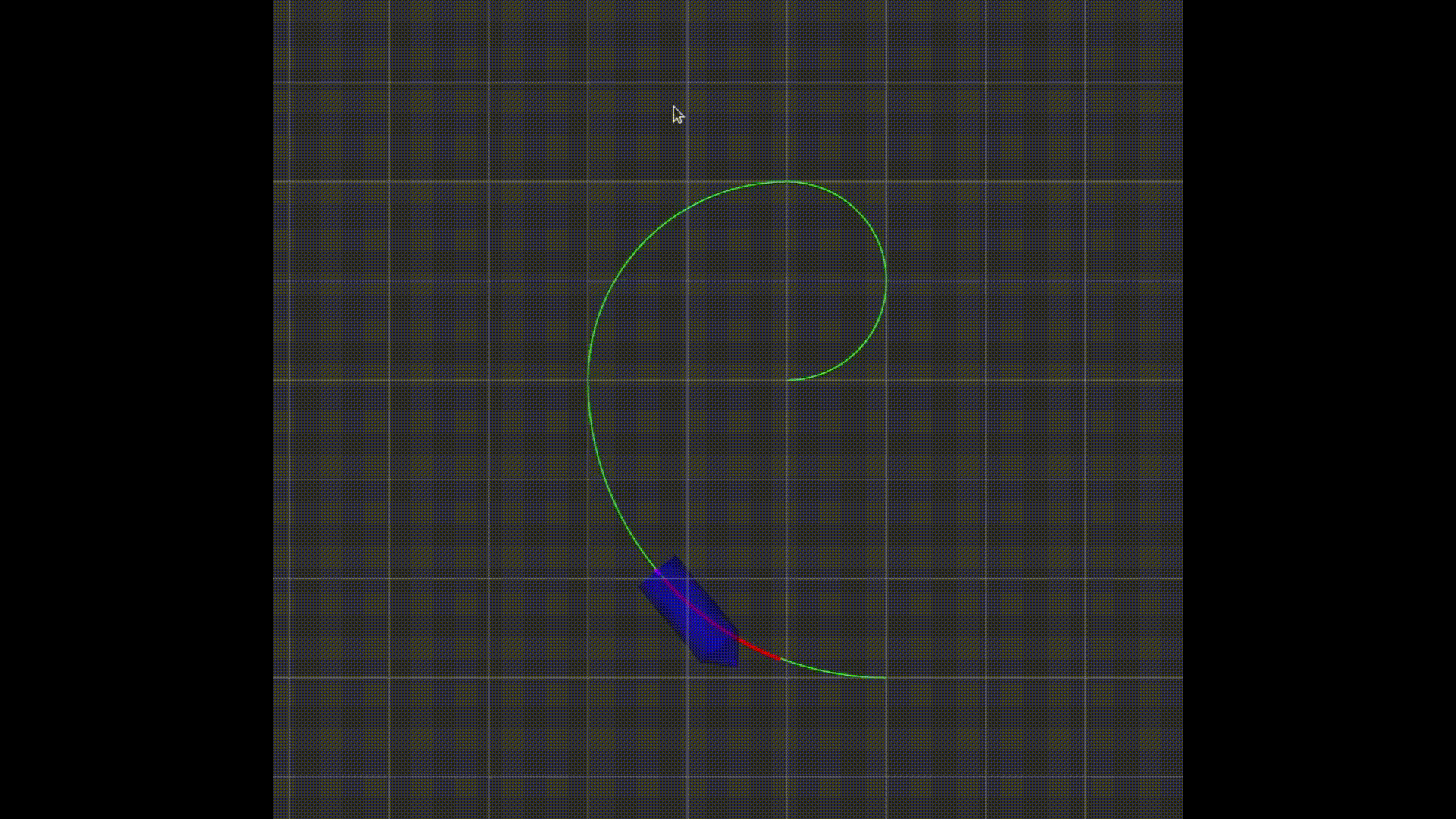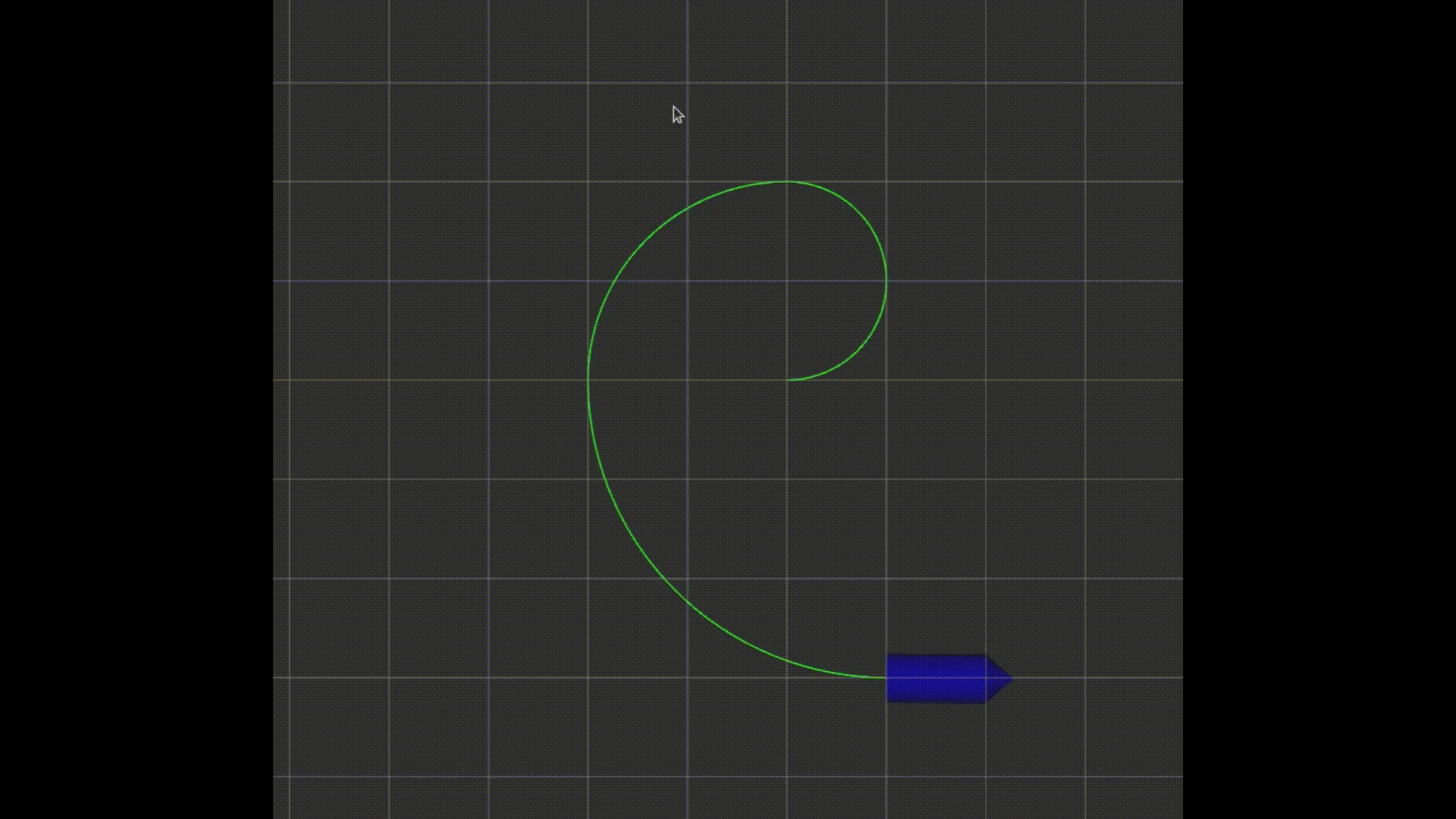
至此，任务完成，小车可以跟踪给定的轨迹。

标签：自动驾驶人工智能机器学习

本文转载自: https://blog.csdn.net/qq_42286607/article/details/124972866
版权归原作者 向南而行灬 所有，如有侵权，请联系我们删除。

MPC（模型预测控制）控制小车沿轨迹移动——C++实现

任务说明

主要流程

运动学自行车模型（Kinematic Bicycle Model）

线性时变模型预测控制（Linear Time-Varying MPC）

动力学系统模型

线性模型

线性时变模型

线性化模型（Model linearization）

设计成本函数（cost function）和约束

设计成本函数

约束

求解二次规划问题

延时模型

发表评论

“MPC（模型预测控制）控制小车沿轨迹移动——C++实现”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航