文章目录
1. DWA(Dynamic window approach)
动态窗口法(DWA)主要是在速度空间中采样多组速度,并模拟机器人在这些速度下一定时间内的轨迹。在得到多组轨迹以后,对这些轨迹进行评价,选取最优轨迹所对应的速度来驱动机器人运动。
1.1 机器人运动模型
动态窗口法将移动机器人的位置控制转换为速度控制。在利用速度模式对机器人运动轨迹进行预测时,首先需要对机器人的运动模型进行分析[1]。移动机器人采用的是两轮差速模型,
v
(
t
)
和
ω
(
t
)
v(t)和ω(t)
v(t)和ω(t)分别代表机器人在世界坐标系下的平移速度与角速度,反映了机器人的运动轨迹。在机器人的编码器采样周期
Δ
t
Δt
Δt内,位移较小,机器人作匀速直线运动,则机器人运动模型为:
x
(
t
)
=
x
(
t
−
1
)
+
v
(
t
)
Δ
t
cos
(
θ
(
t
−
1
)
)
y
(
t
)
=
y
(
t
−
1
)
+
v
(
t
)
Δ
t
sin
(
θ
(
t
−
1
)
)
θ
(
t
)
=
θ
(
t
−
1
)
+
ω
(
t
)
Δ
t
\begin{array}{l}x(t) = x(t - 1) + v(t)\Delta t\cos (\theta (t - 1))\\y(t) = y(t - 1) + v(t)\Delta t\sin (\theta (t - 1))\\\theta (t) = \theta (t - 1) + \omega (t)\Delta t\end{array}
x(t)=x(t−1)+v(t)Δtcos(θ(t−1))y(t)=y(t−1)+v(t)Δtsin(θ(t−1))θ(t)=θ(t−1)+ω(t)Δt式中
x
(
t
)
、
y
(
t
)
、
θ
(
t
)
x(t)、y(t)、θ(t)
x(t)、y(t)、θ(t)———t时刻机器人在世界坐标下的位姿。
1.2 速度采样
动态窗口法将避障问题描述为速度空间中带约束的优化问题,其中约束主要包括差速机器人的非完整约束、环境障碍物的约束以及机器人结构的动力学约束。DWA算法的速度矢量空间示意图如图1-1所示,横坐标为机器人角速度
ω
ω
ω,纵坐标为机器人线速度
v
v
v,其中
v
max
{v_{\max }}
vmax、
v
min
{v_{\min }}
vmin为机器人最大、最小线速度,
ω
max
{\omega _{\max }}
ωmax、
ω
min
{\omega _{\min }}
ωmin为机器人最大、最小角速度;整个区域为
v
s
{v_{s }}
vs,所有白色区域
v
a
{v_{a }}
va为机器人安全区域,
v
d
{v_{d }}
vd为考虑电机扭矩在控制周期内限制的机器人可达速度范围,
v
r
{v_{r }}
vr为上述3个集合的交集最终确定的动态窗口。

图1-1 速度矢量空间示意图
根据机器人的速度限制,定义Vs为机器人线速度与角速度的集合,即动态窗口算法搜索求解的最大范围,满足:
V
s
=
{
(
v
,
ω
)
∣
v
min
≤
v
≤
v
min
,
ω
min
≤
ω
≤
ω
max
}
{V_s} = \{ (v,\omega )|{v_{\min }} \le v \le {v_{\min }},{\omega _{\min }} \le \omega \le {\omega _{\max }}\}
Vs={(v,ω)∣vmin≤v≤vmin,ωmin≤ω≤ωmax} 采样周期
Δ
t
Δt
Δt内存在机器人最大、最小可到达的速度
v
v
v和角速度
ω
ω
ω范围,需要进一步缩小动态窗口。在给定当前线速度
v
c
{v_{c }}
vc和角速度
ω
c
{\omega _{c }}
ωc条件下,下一时刻动态窗口
v
d
{v_{d }}
vd满足:
V
d
=
{
(
v
,
ω
)
∣
v
c
−
v
˙
b
Δ
t
≤
v
≤
v
c
+
v
˙
a
Δ
t
,
ω
c
−
ω
˙
b
Δ
t
≤
ω
≤
ω
c
+
ω
˙
a
Δ
t
}
\begin{array}{r}{V_d} = \{ (v,\omega )|{v_c} - {{\dot v}_b}\Delta t \le v \le {v_c} + {{\dot v}_a}\Delta t,\\{\omega _c} - {{\dot \omega }_b}\Delta t \le \omega \le {\omega _c} + {{\dot \omega }_a}\Delta t\} \end{array}
Vd={(v,ω)∣vc−v˙bΔt≤v≤vc+v˙aΔt,ωc−ω˙bΔt≤ω≤ωc+ω˙aΔt}
式中
v
˙
a
{\dot v_a}
v˙a——机器人最大线加速度;
ω
˙
a
{\dot \omega _a}
ω˙a——机器人最大角加速度;
整个机器人的运动轨迹,可以细分为若干个直线或圆弧运动,为保证机器人安全区域,在最大减速度条件下,当前速度应能在撞击障碍物之前减速为0,则定义机器人碰撞可行区域的线速度与角速度集合
V
a
{V_{a }}
Va满足:
V
a
=
{
(
v
,
ω
)
∣
v
≤
2
d
i
s
t
(
v
,
ω
)
v
˙
b
,
ω
≤
2
d
i
s
t
(
v
,
ω
)
ω
˙
b
}
\begin{array}{r}{V_a} = \{ (v,\omega )|v \le \sqrt {2dist(v,\omega ){{\dot v}_b}} ,\\\omega \le \sqrt {2dist(v,\omega ){{\dot \omega }_b}} \} \end{array}
Va={(v,ω)∣v≤2dist(v,ω)v˙b,ω≤2dist(v,ω)ω˙b}式中
v
˙
b
{\dot v_b}
v˙b ——机器人最大线减速度,
ω
˙
b
{\dot \omega _b}
ω˙b——机器人最大角减速度;
d
i
s
t
(
v
,
ω
)
dist(v,ω)
dist(v,ω)———轨迹上与障碍物最近的距离(如图1-2所示)。
 图1-2
图1-2
d
i
s
t
(
v
,
ω
)
dist(v,ω)
dist(v,ω)———轨迹上与障碍物最近的距离
在速度矢量空间
V
r
{V_{r}}
Vr中,根据线速度、角速度采样点数,将连续的速度矢量空间
V
r
{V_{r}}
Vr离散化,得到离散的采样点
(
v
,
ω
)
(v,ω)
(v,ω)。对于每一个采样点,根据机器人运动学模型预测下一时刻机器人的多个运动轨迹生成,如图1-2所示。

图1-3 机器人多个轨迹生成图
1.3 评价函数
在采样的速度组中,有若干组轨迹是可行的,因此采用评价函数的方式为每条轨迹进行评价,采用的评价函数如下:
G
(
v
,
ω
)
=
σ
(
α
H
e
a
d
i
n
g
(
v
,
ω
)
+
β
O
b
s
t
a
c
l
e
(
v
,
ω
)
+
γ
V
e
l
o
c
i
t
y
(
v
,
ω
)
)
G(v,\omega ) = \sigma (\alpha Heading(v,\omega ) + \beta Obstacle(v,\omega ) + \gamma Velocity(v,\omega ))
G(v,ω)=σ(αHeading(v,ω)+βObstacle(v,ω)+γVelocity(v,ω))
- 方位角评价函数 H e a d i n g ( v , ω ) Heading(v,ω) Heading(v,ω)——方位角不断地朝向终点位置函数。 在移动过程中, H e a d i n g ( v , ω ) Heading(v,ω) Heading(v,ω)函数用于使机器人的朝向不断趋向终点方向, θ θ θ越小,说明与终点的方位角越小。
 图1-4 方位角评价函数示意图
图1-4 方位角评价函数示意图 - 障碍物评价函数 O b s t a c l e ( v , ω ) Obstacle(v,ω) Obstacle(v,ω)——评价机器人轨迹到障碍物距离函数。体现了机器人的避障能力,如果机器人的轨迹到障碍物的距离大于机器人半径,则没有发生碰撞的危险;
 图1-5 障碍物评价函数示意图反之,就说明碰撞风险大,舍弃这条轨迹。
图1-5 障碍物评价函数示意图反之,就说明碰撞风险大,舍弃这条轨迹。 - 速度评价函数 V e l o c i t y ( v , ω ) Velocity(v,ω) Velocity(v,ω)
最后对评价函数进行归一化处理(Why?):
譬如对于障碍物距离评价标准,
机器人传感器检测到的最小障碍物距离在二维空间中是不连续的,这种评价标准将导致评价函数不连续,也会导致某个项在评价函数中太占优势,因此将它们进行平滑处理
。
归一化处理方法: 每一项除以每一项的总和
n
o
r
m
a
l
_
h
e
a
d
(
i
)
=
h
e
a
d
(
i
)
∑
i
=
1
n
h
e
a
d
(
i
)
n
o
r
m
a
l
_
d
i
s
t
(
i
)
=
d
i
s
t
(
i
)
∑
i
=
1
n
d
i
s
t
(
i
)
n
o
r
m
a
l
_
v
o
l
o
c
i
t
y
(
i
)
=
v
o
l
o
c
i
t
y
(
i
)
∑
i
=
1
n
v
o
l
o
c
i
t
y
(
i
)
\begin{array}{c}normal\_head(i) = \frac{{head(i)}}{{\sum\limits_{i = 1}^n {head(i)} }}\\normal\_dist(i) = \frac{{dist(i)}}{{\sum\limits_{i = 1}^n {dist(i)} }}\\normal\_volocity(i) = \frac{{volocity(i)}}{{\sum\limits_{i = 1}^n {volocity(i)} }}\end{array}
normal_head(i)=i=1∑nhead(i)head(i)normal_dist(i)=i=1∑ndist(i)dist(i)normal_volocity(i)=i=1∑nvolocity(i)volocity(i) 其中,
n
n
n为采样的所有轨迹,
i
i
i为待评价的当前轨迹。
三者构成的评价函数的物理意义是:
在局部导航过程中,使得机器人避开障碍,朝着目标以较快速度行驶
。
Dieter Fox[2]在文章中给出了评价指标可视化的图像(图1-6)。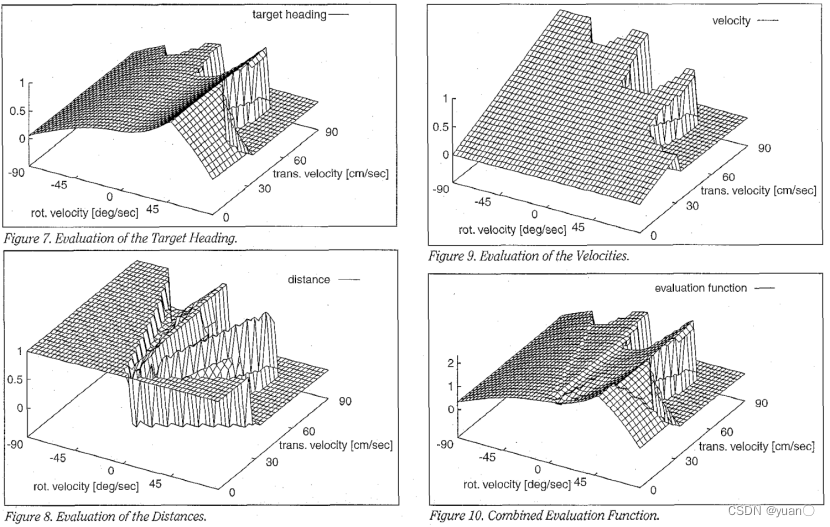
图1-6 评价指标可视化
2. 实践案例——基于ROS实现Astar与DWA算法
本项目以Astar算法作为全局路径规划算法,DWA作为局部路径规划算法,实现效果如下。(具体原理与算法代码解释与说明会在之后的文章附上)
ROS_导航_Astar+DWA
参考文献
[1]劳彩莲,李鹏,冯宇.基于改进A*与DWA算法融合的温室机器人路径规划[J].农业机械学报,2021,52(01):14-22.
[2]Dieter Fox,Wolfram Burgard,Sebastian Thrun. The dynamic window approach to collision avoidance.[J]. IEEE Robot. Automat. Mag.,1997,4(1).
版权归原作者 yuan〇 所有, 如有侵权,请联系我们删除。