0
0

LLM高效推理：KV缓存与分页注意力机制深度解析

随着大型语言模型（LLM）规模和复杂性的持续增长，高效推理的重要性日益凸显。KV（键值）缓存与分页注意力是两种优化LLM推理的关键技术。本文将深入剖析这些概念，阐述其重要性，并探讨它们在仅解码器（decoder-only）模型中的工作原理。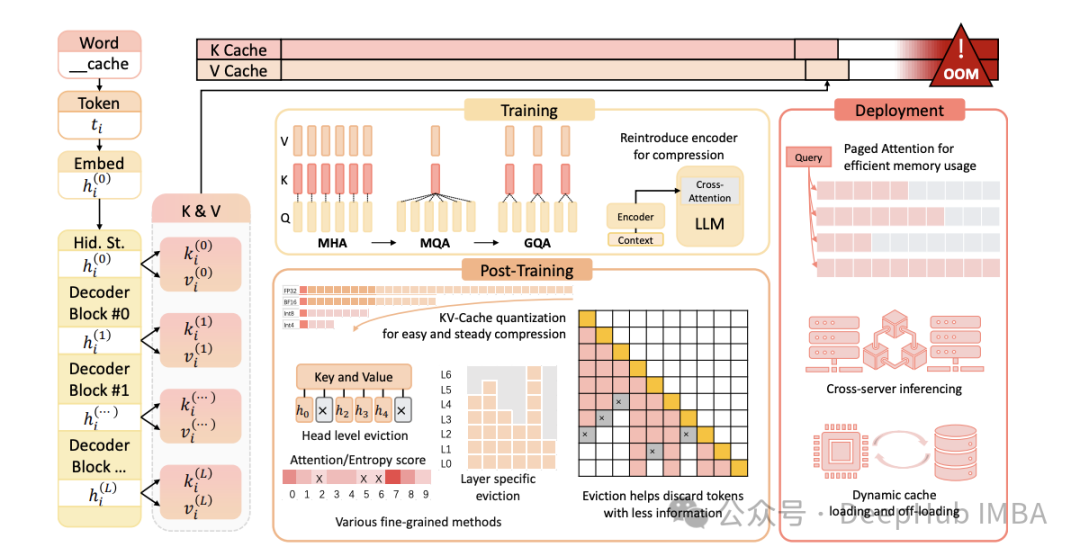

常规推理机制

首先，我们通过一个简单的例子来理解Transformer模型中典型的推理过程。假设我们需要生成短语：

“The quick brown fox jumped”

以下是常规推理的简化实现：

  1.  import numpy as np
  2. # 简化的嵌入表示，仅用于演示
  3. embeddings = {
  4.     'The': np.array([1, 0, 0, 0]),
  5.     'quick': np.array([0, 1, 0, 0]),
  6.     'brown': np.array([0, 0, 1, 0]),
  7.     'fox': np.array([0, 0, 0, 1]),
  8.     'jumped': np.array([1, 1, 0, 0])
  9. }
  11. # 权重矩阵（简化）
  12. W_Q = W_K = W_V = np.array([[1, 0],
  13.     [0, 1],
  14.     [0, 0],
  15.     [0, 0]])
  17. def compute_attention(self, input_words):
  18.     # 将单词转换为嵌入向量
  19.     E = np.array([embeddings[word] for word in input_words])
  21.     # 计算所有token的K和V矩阵
  22.     K = E @ W_K  # 形状: (seq_len, 2)
  23.     V = E @ W_V  # 形状: (seq_len, 2)
  25.     # 计算最后一个token的Q矩阵
  26.     Q = E[-1] @ W_Q  # 形状: (1, 2)
  28.     # 计算缩放的点积注意力得分
  29.     scale = np.sqrt(2)  # 缩放因子，为key/query维度（此处为2）的平方根
  30.     scores = (Q @ K.T) / scale  # 形状: (1, seq_len)
  32.     # 应用Softmax函数，获得注意力权重
  33.     attention_weights = self.softmax(scores)  # 形状: (1, seq_len)
  35.     # 将注意力权重应用于V矩阵
  36.     output = attention_weights @ V  # 形状: (1, 2)
  38.      return output

以下是逐步生成的过程：

  1.  # 步骤1: 生成 "brown"
  2. input_words_step1 = ['The', 'quick']
  3. output_step1 = compute_attention(input_words_step1)
  4. # 步骤2: 生成 "fox"
  5. input_words_step2 = ['The', 'quick', 'brown']
  6. output_step2 = compute_attention(input_words_step2)
  7. # 步骤3: 生成 "jumped"
  8. input_words_step3 = ['The', 'quick', 'brown', 'fox']
  9.  output_step3 = compute_attention(input_words_step3)

冗余计算：观察上述代码可以发现对于每个新生成的token：

  1. 需要为所有先前的token重新计算K和V矩阵。
  2. 矩阵的大小随着token数量的增加而增大。
  3. 存在大量不必要的重复计算。

KV缓存机制

当使用Transformer模型生成文本时，通过缓存键（K）和值（V）矩阵，可以显著优化推理过程。下图展示了KV缓存的工作原理：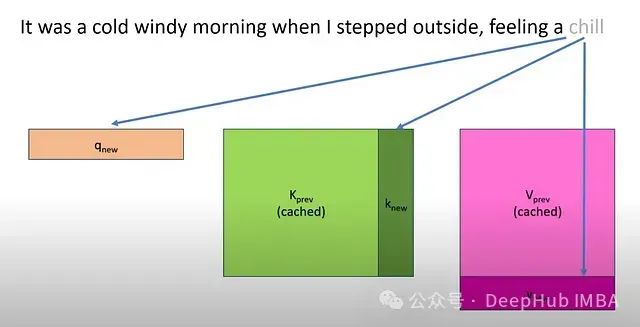

在上图中：

  1. q_new表示最新token的查询向量。
  2. K_prev和V_prev是从先前计算中缓存得到的键和值矩阵。
  3. k_new和v_new仅为当前新token计算。
  4. 蓝色箭头表示如何利用缓存值和新值计算注意力。

以下是KV缓存的实现示例：

  1.  def compute_attention_with_cache(self, input_words):
  2.     """使用KV缓存计算注意力"""
  3.     # 获取新token（序列中的最后一个单词）
  4.     new_word = input_words[-1]
  5.     e_new = embeddings[new_word]
  7.     # 计算新token的K和V矩阵
  8.     K_new = e_new @ W_K  # 形状: (2,)
  9.     V_new = e_new @ W_V  # 形状: (2,)
  11.     # 更新缓存的K和V矩阵
  12.     if self.cached_K is None:
  13.         self.cached_K = K_new.reshape(1, -1)  # 形状: (1, 2)
  14.         self.cached_V = V_new.reshape(1, -1)  # 形状: (1, 2)
  15.     else:
  16.         self.cached_K = np.vstack([self.cached_K, K_new])  # 形状: (seq_len, 2)
  17.         self.cached_V = np.vstack([self.cached_V, V_new])  # 形状: (seq_len, 2)
  19.     # 计算最后一个token的Q矩阵
  20.     Q = e_new @ W_Q  # 形状: (2,)
  22.     # 使用缓存的K矩阵计算缩放的点积注意力得分
  23.     scale = np.sqrt(2)  # 缩放因子，为key/query维度（此处为2）的平方根
  24.     scores = (Q @ self.cached_K.T) / scale  # 形状: (1, seq_len)
  26.     # 应用Softmax函数，获得注意力权重
  27.     attention_weights = self.softmax(scores)  # 形状: (1, seq_len)
  29.     # 使用缓存的V矩阵计算注意力输出
  30.     output = attention_weights @ self.cached_V  # 形状: (1, 2)
  32.      return output

以下是逐步生成的过程：

  1.  # 步骤1: 生成 "brown"
  2. input_words_step1 = ['The', 'quick']
  3. output_step1 = compute_attention_with_cache(input_words_step1)
  4. # 步骤2: 生成 "fox"
  5. input_words_step2 = ['The', 'quick', 'brown']
  6. output_step2 = compute_attention_with_cache(input_words_step2)
  7. # 步骤 3: 生成 "jumped"
  8. input_words_step3 = ['The', 'quick', 'brown', 'fox']
  9.  output_step3 = compute_attention_with_cache(input_words_step3)

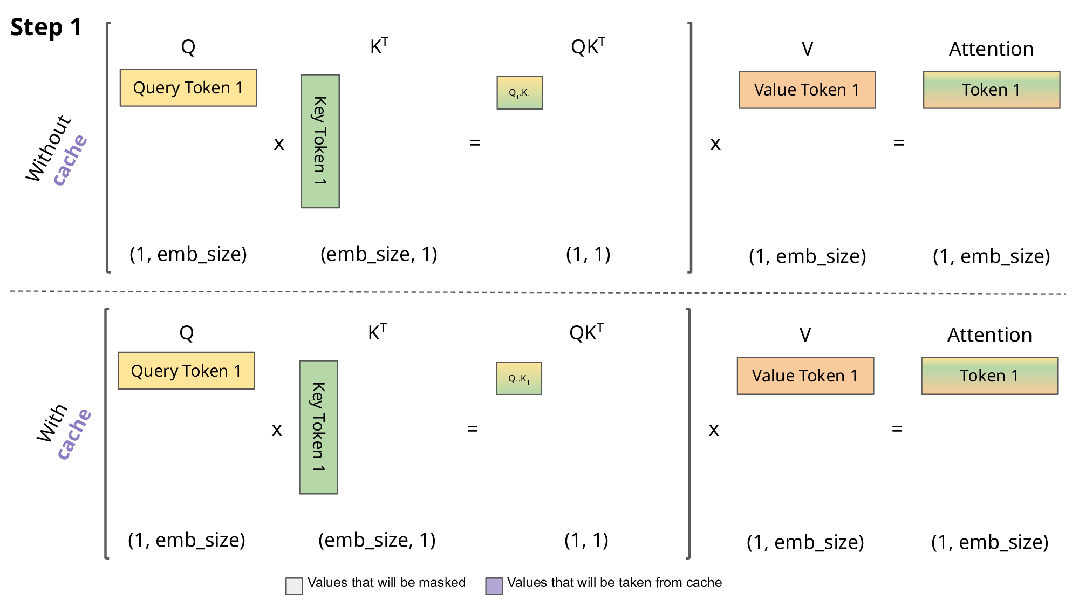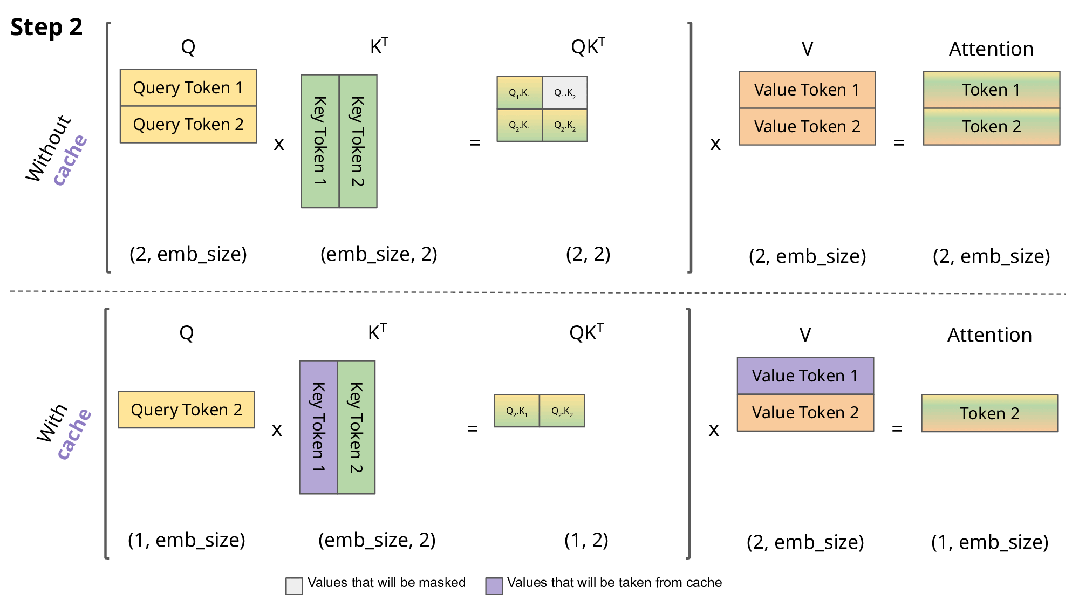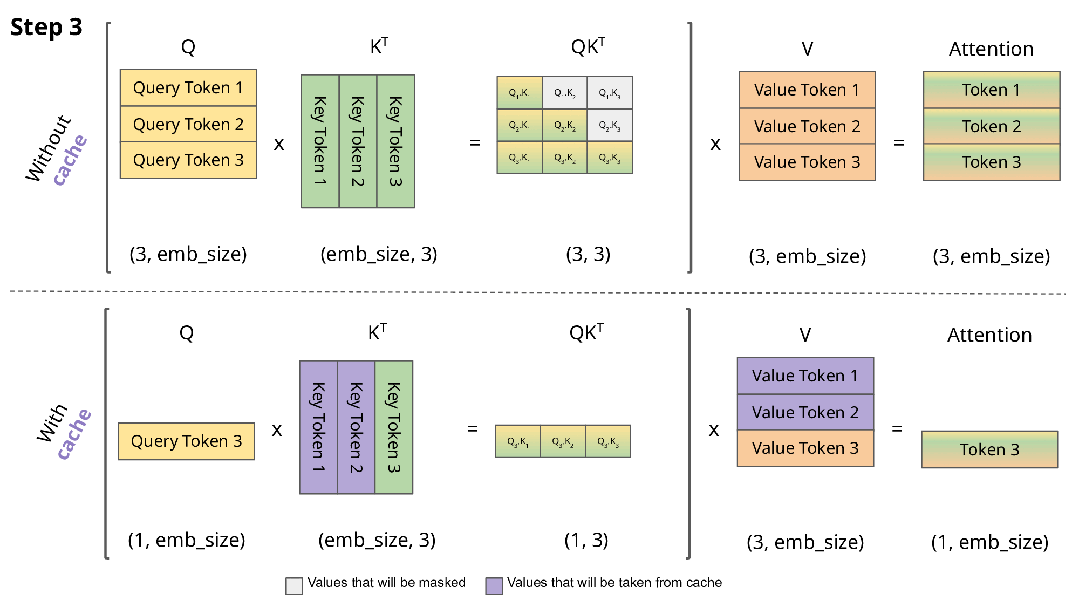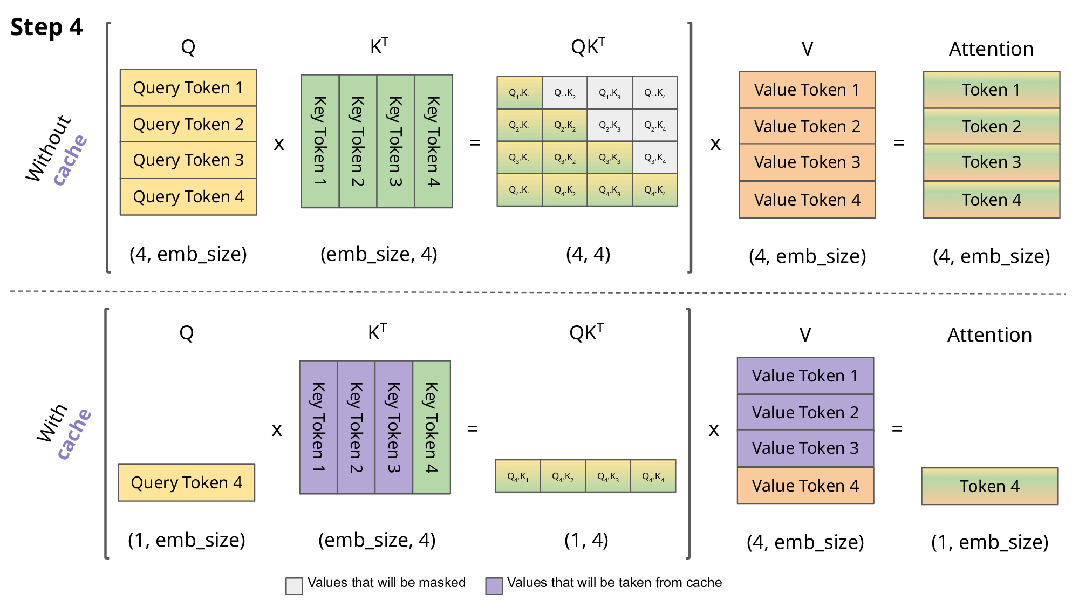
比较有无KV缓存的推理计算

内存需求与挑战

我们来看一个使用典型模型参数的实际例子：

  • 序列长度: 4096
  • 层数: 32
  • 注意力头数: 32
  • 头维度: 128
  • 精度: FP16 (2 bytes)

每个token所需的内存：

  1.  KV_cache_per_token = 2×num_layers×(num_heads×head_dim)×precision
  2.  = 2 × 32 × (32 × 128) × 2 bytes
  3.  = 2 × 32 × 4096 × 2 bytes
  4.  = 524,288 bytes
  5.  ≈ 0.5 MB

KV缓存的低效性

尽管KV缓存显著提高了计算效率，但它也带来了内存管理方面的挑战。以下是三种主要的内存低效类型：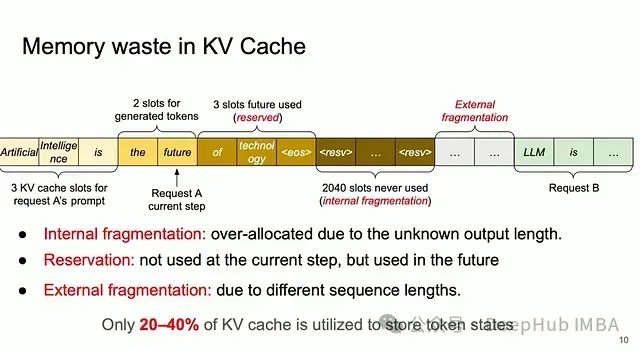

内部碎片

  • 由因未知输出长度而导致的过度分配引起。
  • 示例：在图像中，2040个槽位从未被使用。
  • 影响：可能浪费高达60-80％的已分配内存。
  • 解决方案：更精确的输出长度估计或动态分配策略。

预留浪费

  • 为将来的token生成而预留的内存。
  • 在图像中显示为“3 slots future used (reserved)”。
  • 维持生成连续性的必要措施。
  • 可以通过更好地预测所需的未来槽位来优化。

外部碎片

  • 由处理具有不同序列长度的多个请求导致。
  • 在不同请求之间创建内存间隙。
  • 解决方案包括内存碎片整理和智能请求批处理。

如上图所示，通常仅有20-40％的KV缓存被用于存储实际的token状态。

分页注意力：解决内存低效的方案

为了应对这些内存挑战，可以采用分页注意力机制。

分页注意力是一种用于有效处理Transformer模型中长序列的技术，它通过将注意力计算分解为更小、更易于管理的“页”或“块”来实现。这种方法降低了内存消耗和计算复杂度，从而能够处理原本因过大而无法放入内存的序列。

  1.  def compute_attention_with_paging(self, input_words):
  2.     """使用分页KV缓存计算注意力"""
  3.     # 获取新token（序列中的最后一个单词）
  4.     new_word = input_words[-1]
  5.     e_new = embeddings[new_word]
  7.     # 计算新token的K和V矩阵
  8.     K_new = e_new @ W_K  # 形状: (2,)
  9.     V_new = e_new @ W_V  # 形状: (2,)
  11.     # 确定当前页的索引
  12.     total_tokens = sum(len(K_page) for K_page in self.cached_K_pages) + 1
  13.     current_page_idx = (total_tokens - 1) // PAGE_SIZE
  15.     # 如果需要，初始化新页
  16.     if len(self.cached_K_pages) <= current_page_idx:
  17.         self.cached_K_pages.append([])
  18.         self.cached_V_pages.append([])
  20.     # 将K和V添加到当前页的缓存中
  21.     self.cached_K_pages[current_page_idx].append(K_new)
  22.     self.cached_V_pages[current_page_idx].append(V_new)
  24.     # 计算当前token的Q矩阵
  25.     Q = e_new @ W_Q  # Shape: (2,)
  27.     # 仅在当前页内计算注意力
  28.     K_current_page = np.array(self.cached_K_pages[current_page_idx])
  29.     V_current_page = np.array(self.cached_V_pages[current_page_idx])
  31.     # 添加缩放因子，用于点积注意力
  32.     scale = np.sqrt(2)  # 缩放因子，为key/query维度（此处为2）的平方根
  33.     scores = (Q @ K_current_page.T) / scale
  35.     # 应用Softmax函数，获得注意力权重
  36.     attention_weights = self.softmax(scores)  # 形状: (1, current_page_size)
  38.     # 将注意力权重应用于当前页中的V矩阵
  39.     output = attention_weights @ V_current_page
  41.      return output

以下是逐步生成的过程：

  1.  # 步骤1: 生成 "brown"
  2. input_words_step1 = ['The', 'quick']
  3. output_step1 = compute_attention_with_paging(input_words_step1)
  4. # 步骤2: 生成 "fox"
  5. input_words_step2 = ['The', 'quick', 'brown']
  6. output_step2 = compute_attention_with_paging(input_words_step2)
  7. # 步骤3: 生成 "jumped"
  8. input_words_step3 = ['The', 'quick', 'brown', 'fox']
  9.  output_step3 = compute_attention_with_paging(input_words_step3)

为何需要分页注意力？

  • 内存约束：由于注意力矩阵的规模与序列长度呈平方关系，Transformer模型在处理长序列时面临严重的内存限制。
  • 长序列处理：在诸如语言建模或文档摘要等任务中，序列可能非常长。
  • 效率：通过以分页的方式处理注意力计算，可以将内存使用量保持在一个常量水平，从而不受序列长度的影响。

分页注意力如何工作？

  • 分割序列：将输入序列分割成更小的块或页。
  • 局部注意力：在每个页内计算注意力。
  • 跨页注意力：可选地，允许有限的跨页注意力，以捕获页之间的依赖关系。
  • 滑动窗口：使用重叠的页来确保连续性。

上述实现仅限于局部注意力，跨页注意力和滑动窗口的实现超出了本文的范围，将在后续文章中详细介绍。

分页注意力的讨论

优势

  • 内存效率：注意力计算被限制在页大小内，内存使用量保持恒定，不受总序列长度的影响。
  • 计算效率：降低了注意力计算的复杂度。
  • 可扩展性：能够处理原本无法放入内存的超长序列。

权衡与考虑

  • 上下文信息受限：模型会丢失跨页的一些依赖关系，这对于需要全局上下文的任务可能很重要。

可能的解决方案：

  • 重叠页：允许页之间重叠一定数量的token，重叠区域的token可以关注前一页的token。
  • 分层注意力：使用更高层次的注意力机制来连接跨页的信息。

重叠页、分层注意力、跨页注意力和滑动窗口的完整实现超出了本文的范围。

以下实现仅捕获局部注意力，作为示例不应在实际应用中使用：

  1.  # 本实现仅为演示和理解目的而设计的简化版本。
  2. # 实际应用中需要更高效和可扩展的实现。
  4. import numpy as np
  6. embeddings = {
  7.     'The': np.array([1, 0, 0, 0]),
  8.     'quick': np.array([0, 1, 0, 0]),
  9.     'brown': np.array([0, 0, 1, 0]),
  10.     'fox': np.array([0, 0, 0, 1]),
  11.     'jumped': np.array([1, 1, 0, 0])
  12. }
  14. W_Q = W_K = W_V = np.array([[1, 0],
  15.                             [0, 1],
  16.                             [0, 0],
  17.                             [0, 0]])
  19. PAGE_SIZE = 2  # 演示用的小页尺寸
  21. class AttentionWithCache:
  22.     def __init__(self):
  23.         self.cached_K = None  # 形状: (seq_len, 2)
  24.         self.cached_V = None  # 形状: (seq_len, 2)
  25.         self.cached_K_pages = []  # 包含K向量的页列表
  26.         self.cached_V_pages = []  # 包含V向量的页列表
  28.     def softmax(self, x, axis=-1):
  29.         """
  30.         为x中的每组分数计算Softmax值。
  31.         包含数值稳定性改进。
  32.         """
  33.         # 应用最大值减法以提高数值稳定性
  34.         x_max = np.max(x, axis=axis, keepdims=True)
  35.         exp_x = np.exp(x - x_max)
  36.         return exp_x / np.sum(exp_x, axis=axis, keepdims=True)
  38.     def compute_attention(self, input_words):
  39.         # 将单词转换为嵌入向量
  40.         E = np.array([embeddings[word] for word in input_words])
  42.         # 计算所有token的K和V矩阵
  43.         K = E @ W_K  # 形状: (seq_len, 2)
  44.         V = E @ W_V  # 形状: (seq_len, 2)
  46.         # 计算最后一个token的Q矩阵
  47.         Q = E[-1] @ W_Q  # 形状: (1, 2)
  49.         # 计算缩放的点积注意力得分
  50.         scale = np.sqrt(2)  # 缩放因子，为key/query维度（此处为2）的平方根
  51.         scores = (Q @ K.T) / scale  # 形状: (1, seq_len)
  53.         # 应用Softmax函数，获得注意力权重
  54.         attention_weights = self.softmax(scores)  # 形状: (1, seq_len)
  56.         # 将注意力权重应用于V矩阵
  57.         output = attention_weights @ V  # 形状: (1, 2)
  59.         return output
  61.     def compute_attention_with_cache(self, input_words):
  62.         """使用KV缓存计算注意力"""
  63.         # 获取新token（序列中的最后一个单词）
  64.         new_word = input_words[-1]
  65.         e_new = embeddings[new_word]
  67.         # 计算新token的K和V矩阵
  68.         K_new = e_new @ W_K  # 形状: (2,)
  69.         V_new = e_new @ W_V  # 形状: (2,)
  71.         # 更新缓存的K和V矩阵
  72.         if self.cached_K is None:
  73.             self.cached_K = K_new.reshape(1, -1)  # 形状: (1, 2)
  74.             self.cached_V = V_new.reshape(1, -1)  # 形状: (1, 2)
  75.         else:
  76.             self.cached_K = np.vstack([self.cached_K, K_new])  # 形状: (seq_len, 2)
  77.             self.cached_V = np.vstack([self.cached_V, V_new])  # 形状: (seq_len, 2)
  79.         # 计算最后一个token的Q矩阵
  80.         Q = e_new @ W_Q  # 形状: (2,)
  82.         # 使用缓存的K矩阵计算缩放的点积注意力得分
  83.         scale = np.sqrt(2)  # 缩放因子，为key/query维度（此处为2）的平方根
  84.         scores = (Q @ self.cached_K.T) / scale  # 形状: (1, seq_len)
  86.         # 应用Softmax函数，获得注意力权重
  87.         attention_weights = self.softmax(scores)  # 形状: (1, seq_len)
  89.         # 使用缓存的V矩阵计算注意力输出
  90.         output = attention_weights @ self.cached_V  # 形状: (1, 2)
  92.         return output
  94.     def compute_attention_with_paging(self, input_words):
  95.         """使用分页KV缓存计算注意力"""
  96.         # 获取新token（序列中的最后一个单词）
  97.         new_word = input_words[-1]
  98.         e_new = embeddings[new_word]
  100.         # 计算新token的K和V矩阵
  101.         K_new = e_new @ W_K  # 形状: (2,)
  102.         V_new = e_new @ W_V  # 形状: (2,)
  104.         # 确定当前页的索引
  105.         total_tokens = sum(len(K_page) for K_page in self.cached_K_pages) + 1
  106.         current_page_idx = (total_tokens - 1) // PAGE_SIZE
  108.         # 如果需要，初始化新页
  109.         if len(self.cached_K_pages) <= current_page_idx:
  110.             self.cached_K_pages.append([])
  111.             self.cached_V_pages.append([])
  113.         # 将K和V添加到当前页的缓存中
  114.         self.cached_K_pages[current_page_idx].append(K_new)
  115.         self.cached_V_pages[current_page_idx].append(V_new)
  117.         # 计算当前token的Q矩阵
  118.         Q = e_new @ W_Q  # Shape: (2,)
  120.         # 仅在当前页内计算注意力
  121.         K_current_page = np.array(self.cached_K_pages[current_page_idx])
  122.         V_current_page = np.array(self.cached_V_pages[current_page_idx])
  124.         # 添加缩放因子，用于点积注意力
  125.         scale = np.sqrt(2)  # 缩放因子，为key/query维度（此处为2）的平方根
  126.         scores = (Q @ K_current_page.T) / scale
  128.         # 应用Softmax函数，获得注意力权重
  129.         attention_weights = self.softmax(scores)  # 形状: (1, current_page_size)
  131.         # 将注意力权重应用于当前页中的V矩阵
  132.         output = attention_weights @ V_current_page
  134.         return output
  136. def compare_implementations():
  137.     print("原始实现:")
  138.     attention1 = AttentionWithCache()
  140.     # 使用原始方法处理序列
  141.     for i in range(len(['The', 'quick', 'brown', 'fox'])):
  142.         words = ['The', 'quick', 'brown', 'fox'][:i + 1]
  143.         output = attention1.compute_attention(words)
  144.         print(f"处理 {words} 后的输出:")
  145.         print(f"Output: {output}")
  147.     print("\nKV缓存实现:")
  148.     attention2 = AttentionWithCache()
  150.     # 使用KV缓存处理序列
  151.     for i in range(len(['The', 'quick', 'brown', 'fox'])):
  152.         words = ['The', 'quick', 'brown', 'fox'][:i + 1]
  153.         output = attention2.compute_attention_with_cache(words)
  154.         print(f"处理 {words} 后的输出:")
  155.         print(f"Output: {output}")
  157.     print("\n分页注意力实现:")
  158.     attention3 = AttentionWithCache()
  160.     # 使用分页注意力处理序列
  161.     for i in range(len(['The', 'quick', 'brown', 'fox'])):
  162.         words = ['The', 'quick', 'brown', 'fox'][:i + 1]
  163.         output = attention3.compute_attention_with_paging(words)
  164.         print(f"处理 {words} 后的输出:")
  165.         print(f"Output: {output}")
  166.         print(f"页数: {len(attention3.cached_K_pages)}")
  167.         print(f"当前页大小: {len(attention3.cached_K_pages[-1])}\n")
  169. if __name__ == "__main__":
  170.      compare_implementations()

总结

KV缓存和分页注意力是提升LLM推理效率和可扩展性的重要技术。KV缓存通过消除冗余计算来优化计算过程，而分页注意力则解决了处理长序列时面临的内存限制。

随着模型规模和复杂性的不断增长，这些优化技术对于实际应用变得至关重要。深入理解和有效实施这些技术，可以显著提升LLM部署的性能和效率。

作者：Dewang Sultania

标签： 深度学习 LLM 注意力机制
登录后发布评论

“LLM高效推理：KV缓存与分页注意力机制深度解析”的评论:

还没有评论
关于作者
...
Deephub
更多文章请关注公众号：Deephub-IMBA
相关阅读

标签噪声下的模型评估：如何准确评估AI模型的真实性能，提高模型性能测量的可信度

VideoMind：Chain-of-LoRA突破时间盲区让AI真正看懂长视频

9个主流GAN损失函数的数学原理和Pytorch代码实现：从经典模型到现代变体

DAPO: 面向开源大语言模型的解耦裁剪与动态采样策略优化系统

多模态AI核心技术：CLIP与SigLIP技术原理与应用进展

SWEET-RL：基于训练时信息的多轮LLM代理强化学习框架

时间序列异常检测：MSET-SPRT组合方法的原理和Python代码实现