
**个人简介: **
📦个人主页:赵四司机
🏆学习方向:JAVA后端开发
⏰往期文章:SpringBoot项目整合微信支付
🔔博主推荐网站:牛客网 刷题|面试|找工作神器
📣种一棵树最好的时间是十年前,其次是现在!
💖喜欢的话麻烦点点关注喔,你们的支持是我的最大动力。
前言:
通过这篇文章你将了解线性滤波器在数字图像处理中的应用并且理解图像滤波器的处理过程和处理前后图像的变化关系。
一:滤波器原理
线性低通滤波器是最常用的线性平滑滤波器。这种滤波器的所有系数都是正的。对3*3的模板来说,最简单的是取所有系数都为1。为保证输出图像仍在原来的灰度范围,在计算出算子后要将其除以9再进行赋值。这种方法称为邻域平均法。
**维纳滤波**也是经典的线性降噪滤波器。维纳滤波是一种自适应滤波,它能根据图像的局部方差调整滤波器的输出。局部方差越大,滤波器的平滑作用越强。它的最终目标是使恢复图像f*(x,y)与原图像f(x,y)的均方误差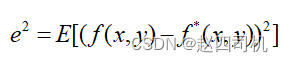 最小。
** 中值滤波器**是最常用的非线性平滑滤波器。它是一种邻域运算,类似于卷积,但计算的不是加权求和,而是把邻域中的像素按灰度级进行排序,然后选择该组的中间值作为输出像素值。具体步骤是:
(1)将模板在图像中漫游,并将模板中心与图像中某个像素的位置重合;
(2)读取模板下各对应像素的灰度值;
(3)将这些灰度值从小到大排成一列,找出这些值里排在中间的一个;
(4)将这个中间值赋给对应模板中心位置的像素。
由此可以看出,中值滤波器的主要功能就是让与周围像素灰度值的差比较大的像素改取与周围的像素值接近的值,从而可以消除孤立的噪声点。中值滤波器不像均值滤波器那样,它在衰减噪声的同时不会使图像的边界模糊,这也是中值滤波受欢迎的主要原因。中值滤波器去噪声的效果依赖于两个要素:邻域的空间范围和中值计算中所涉及的像素数。一般来说,小于中值滤波器面积一半的亮或暗的物体基本上会被滤掉,而较大的物体则几乎会原封不动地保存下来。因此,中值滤波器的空间尺寸必须根据现有的问题来进行调整。较简单的模板是 的方形(这里N常是奇数),计算使用到的所有 各像素点。另外,我们也可以使用稀疏分布的模板来节省时间。对于不同的模板,中值也要依情况而定。计算中值所使用的像素的增加跟去噪时的效果之间的关系是非线性的。如果现在的问题需要用到大尺度的中值滤波器,那么用稀疏分布的中值模板或许能得到令人满意的效果。
二:代码实现
1.均值滤波
(1)对参考图像实现均值滤波器滤波操作,需要添加相关噪声
I=imread('lena.png');
J=imnoise(I,'salt',0.02);
figure ,subplot(2,2,1),imshow(I),title('原图像');
subplot(2,2,2),imshow(J),title('加入椒盐噪声的图像');
K1=filter2(fspecial('average',3),J)/255;
%的均值滤波处理结果
K2=filter2(fspecial('average',5),J)/255;
%的均值滤波处理结果
subplot(2,2,3),imshow(K1),
title('的均值滤波处理结果');
subplot(2,2,4),imshow(K2),
title('的均值滤波处理结果');

图1.3.1-1 均值滤波处理结果
分析:均值滤波是将图像中的一块区域中心点的像素变成该区域所有像素的均值,fspecial()函数用于创建均值滤波器,可以指定其创建的滤波器大小,默认为3*3。对于处理结果,可以看到其去噪效果并不是很好,还有一些噪声没有去除,特别是当均值滤波器较小的时候(见图1.3.1-1左下),增大均值滤波器可以看到噪声被去除得较多,但是仍有噪声可见,而且图像的质量也随之变差了,因为均值滤波会将图像边缘和特征信息“模糊”掉。
(2)使用高斯和维纳滤波器进行降噪处理
I=imread('image\lena.png');
J=imnoise(I,'gaussian',0,0.005);
h=fspecial('gaussian');
K=filter2(h,J)/255;
K1=wiener2(J,[5,5]);
K2=filter2(fspecial('average',5),J)/255; %5*5的均值滤波处理结果
figure, subplot(2,3,1),imshow(I),title('原图像');
subplot(2,3,2),imshow(J),title('加入高斯噪声的图像');
subplot(2,3,3),imshow(K),title('高斯低通滤波的结果');
subplot(2,3,4),imshow(K1),title('维纳滤波后的结果');
subplot(235),imshow(K2),title('均值滤波处理高斯噪声的结果');
%自编程实现高斯低通滤波器
d0=80; %截止频率
[M ,N]=size(J);
img_f = fft2(double(J));%傅里叶变换得到频谱
img_f=fftshift(img_f); %移到中间
m_mid=floor(M/2);%中心点坐标
n_mid=floor(N/2);
h = zeros(M,N);%高斯低通滤波器构造
for i = 1:M
for j = 1:N
d = ((i-m_mid)^2+(j-n_mid)^2);
h(i,j) = exp(-(d)/(2*(d0^2)));
end
end
img_lpf = h.*img_f;
img_lpf=ifftshift(img_lpf); %中心平移回原来状态
img_lpf=uint8(real(ifft2(img_lpf))); %反傅里叶变换,取实数部分
subplot(236);imshow(img_lpf);title('自编程实现高斯低通滤波d0=80');

图1.3.2-1 各种滤波器进行降噪处理结果
低通滤波器仅保留低频分量而过滤掉高频分量,噪声一般分布在高频分量,所以可以通过这样来达到过滤噪声的目的。程序通过fspecial('gaussian')函数生成高斯低通滤波器,然后通过filter2对目标矩阵进行有限脉冲响应滤波,高斯低通滤波传输函数定义为:
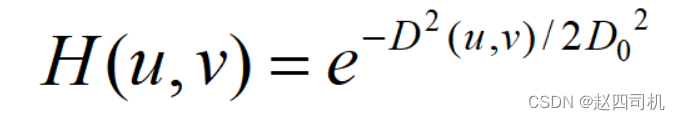
其中D0表示截止频率,D表示每一个像素距离中心点坐标的距离,根据该公式可以自编程实现高斯低通滤波器(代码见上面代码区),通过设定不同的截止频率可以得到不同的效果,可以看到当截止频率设定为80时候,处理得出的图像要比matlab自带的函数得到的结果要好。
此外,通过实验第一小点可以看到均值滤波处理椒盐噪声的效果不是很好,网上说均值滤波对高斯噪声的处理结果较好,在程序中加入5*5的均值滤波处理高斯噪声,可以看到其处理效果和维纳滤波处理的结果相差不大,效果较好。
对于维纳滤波,它是一种基于最小均方误差准则、对平稳过程的最优估计器。这种滤波器的输出与期望输出之间的均方误差为最小,因此,它是一个最佳滤波系统,通过使均方误差最小来进行降噪处理,可以看到处理结果在所有测试的滤波器中是最好的(见图1.3.2-1)。
2.中值滤波
(1)使用例子图片实现中值过滤器(3*3模板)
%非线性平滑滤波器
%加入椒盐噪声并采用模板实现中值过滤器
I=imread('peppers.png);
J=imnoise(I,'salt',0.02);
figure ,subplot(2,2,1),imshow(I),title('原图像');
subplot(2,2,2),imshow(J),title('加入椒盐噪声后的图像');
K1=medfilt2(J,[3,3]);% 用模板实现中值过滤器
subplot(2,2,3),imshow(K1),title('中值滤波后的结果');
%自编程:
%自编程实现中值滤波
clear;
n=5; %模板大小
image = imread('peppers.png');
I=rgb2gray(image);
J=imnoise(I,'salt',0.02);
[height, width] = size(J); %获取图像尺寸
FilterMid = J;
for row = (n+1)/2:height-(n-1)/2
for col = (n+1)/2:width-(n-1)/2
temp=double(J(row-((n-1)/2):row+((n-1)/2),... col-((n-1)/2):col+((n-1)/2))); %获取模板区域(接上一行)
%中值滤波
template2 = sort(temp(:)); %对模板区域内像素值进行排序
FilterMid(row, col) = template2((n*n+1)/2); %更新模板中心像素值
end
end
figure ,subplot(1,3,1),imshow(I),title('原图像');
subplot(1,3,2),imshow(J),title('加入椒盐噪声后的图像');
subplot(1,3,3),imshow(FilterMid),title('中值滤波后的结果');

图1.3.3-1 中值滤波实验结果
分析:中值滤波是一种基于排序的非线性平滑滤波算法,相比于均值滤波,均值滤波对噪声处理是一种模糊化处理,因而容易破坏图像的细节及轮廓,但是中值滤波却能在不破坏图像细节的前提下做到有效去除噪声(特别是椒盐噪声)。
了解中值滤波原理后,很容易就能自编程实现中值滤波器(代码见上面代码部分),在选取模板为3*3时候,边界不作处理也不会出现明显的噪声,但是当模板变为5*5时,由于没对边界处理,图像四周没有发生变化,原来的噪声没有被消除(见图1.3.3-1)。可以通过在边界填充0或者填充最近像素来进行处理。
3.不同滤波器比较
分别用不同的三张图片,比较不同窗口(模板)大小,至少5种,分别加入高斯噪声,椒盐噪声 (可选加入:指数分布噪声,泊松噪声,乘性噪声),比较不同模板大小,不同噪声下的使用均值滤波器,高斯滤波器,维纳滤波和中值滤波的效果。
image1=imread('pout.tif');
imshow(image1),title('pout原图');
I1=imnoise(image1,'gaussian',0,0.005); %加入高斯噪声
I2=imnoise(image1,'salt',0.02); %加入椒盐噪声
K1_1=filter2(fspecial('average',3),I1)/255; %3*3的均值滤波处理(高斯噪声)结果
K1_2=filter2(fspecial('average',3),I2)/255; %3*3的均值滤波处理(椒盐噪声)结果
K2_1=filter2(fspecial('average',5),I1)/255; %5*5的均值滤波处理(高斯噪声)结果
K2_2=filter2(fspecial('average',5),I2)/255; %5*5的均值滤波处理(椒盐噪声)结果
K3_1=filter2(fspecial('average',7),I1)/255; %7*7的均值滤波处理(高斯噪声)结果
K3_2=filter2(fspecial('average',7),I2)/255; %7*7的均值滤波处理(椒盐噪声)结果
K4_1=filter2(fspecial('average',8),I1)/255; %8*8的均值滤波处理(高斯噪声)结果
K4_2=filter2(fspecial('average',8),I2)/255; %8*8的均值滤波处理(椒盐噪声)结果
K5_1=filter2(fspecial('average',9),I1)/255; %9*9的均值滤波处理(高斯噪声)结果
K5_2=filter2(fspecial('average',9),I2)/255; %9*9的均值滤波处理(椒盐噪声)结果
figure,subplot(3,4,1),imshow(I1),title('pout图像加入高斯噪声');
subplot(3,4,2),imshow(I2),title('pout图像加入椒盐噪声');
subplot(3,4,3),imshow(K1_1),title('3*3的均值滤波处理(高斯噪声)结果');
subplot(3,4,4),imshow(K1_2),title('3*3的均值滤波处理(椒盐噪声)结果');
subplot(3,4,5),imshow(K2_1),title('5*5的均值滤波处理(高斯噪声)结果');
subplot(3,4,6),imshow(K2_2),title('5*5的均值滤波处理(椒盐噪声)结果');
subplot(3,4,7),imshow(K3_1),title('7*7的均值滤波处理(高斯噪声)结果');
subplot(3,4,8),imshow(K3_2),title('7*7的均值滤波处理(椒盐噪声)结果');
subplot(3,4,9),imshow(K4_1),title('8*8的均值滤波处理(高斯噪声)结果');
subplot(3,4,10),imshow(K4_2),title('8*8的均值滤波处理(椒盐噪声)结果');
subplot(3,4,11),imshow(K5_1),title('9*9的均值滤波处理(高斯噪声)结果');
subplot(3,4,12),imshow(K5_2),title('9*9的均值滤波处理(椒盐噪声)结果');
h1=fspecial('gaussian',[3,3],0.5);
h2=fspecial('gaussian',[5,5],0.5);
h3=fspecial('gaussian',[7,7],0.5);
h4=fspecial('gaussian',[8,8],0.5);
h5=fspecial('gaussian',[9,9],0.5);
K1_1=filter2(h1,I1)/255; %窗口为3*3的高斯滤波处理高斯噪声
K1_2=filter2(h1,I2)/255; %窗口为3*3的高斯滤波处理椒盐噪声
K2_1=filter2(h2,I1)/255; %窗口为5*5的高斯滤波处理高斯噪声
K2_2=filter2(h2,I2)/255; %窗口为5*5的高斯滤波处理椒盐噪声
K3_1=filter2(h3,I1)/255; %窗口为7*7的高斯滤波处理高斯噪声
K3_2=filter2(h3,I2)/255; %窗口为7*7的高斯滤波处理椒盐噪声
K4_1=filter2(h4,I1)/255; %窗口为8*8的高斯滤波处理高斯噪声
K4_2=filter2(h4,I2)/255; %窗口为8*8的高斯滤波处理椒盐噪声
K5_1=filter2(h5,I1)/255; %窗口为9*9的高斯滤波处理高斯噪声
K5_2=filter2(h5,I2)/255; %窗口为9*9的高斯滤波处理椒盐噪声
figure,subplot(3,4,1),imshow(I1),title('pout图像加入高斯噪声');
subplot(3,4,2),imshow(I2),title('pout图像加入椒盐噪声');
subplot(3,4,3),imshow(K1_1),title('3*3的高斯滤波处理(高斯噪声)结果');
subplot(3,4,4),imshow(K1_2),title('3*3的高斯滤波处理(椒盐噪声)结果');
subplot(3,4,5),imshow(K2_1),title('5*5的高斯滤波处理(高斯噪声)结果');
subplot(3,4,6),imshow(K2_2),title('5*5的高斯滤波处理(椒盐噪声)结果');
subplot(3,4,7),imshow(K3_1),title('7*7的高斯滤波处理(高斯噪声)结果');
subplot(3,4,8),imshow(K3_2),title('7*7的高斯滤波处理(椒盐噪声)结果');
subplot(3,4,9),imshow(K4_1),title('8*8的高斯滤波处理(高斯噪声)结果');
subplot(3,4,10),imshow(K4_2),title('8*8的高斯滤波处理(椒盐噪声)结果');
subplot(3,4,11),imshow(K5_1),title('9*9的高斯滤波处理(高斯噪声)结果');
subplot(3,4,12),imshow(K5_2),title('9*9的高斯滤波处理(椒盐噪声)结果');
K1_1=wiener2(I1,[3,3]);
K1_2=wiener2(I2,[3,3]);
K2_1=wiener2(I1,[5,5]);
K2_2=wiener2(I2,[5,5]);
K3_1=wiener2(I1,[7,7]);
K3_2=wiener2(I2,[7,7]);
K4_1=wiener2(I1,[8,8]);
K4_2=wiener2(I2,[8,8]);
K5_1=wiener2(I1,[9,9]);
K5_2=wiener2(I2,[9,9]);
figure,subplot(3,4,1),imshow(I1),title('pout图像加入高斯噪声');
subplot(3,4,2),imshow(I2),title('pout图像加入椒盐噪声');
subplot(3,4,3),imshow(K1_1),title('3*3的维纳滤波处理(高斯噪声)结果');
subplot(3,4,4),imshow(K1_2),title('3*3的维纳滤波处理(椒盐噪声)结果');
subplot(3,4,5),imshow(K2_1),title('5*5的维纳滤波处理(高斯噪声)结果');
subplot(3,4,6),imshow(K2_2),title('5*5的维纳滤波处理(椒盐噪声)结果');
subplot(3,4,7),imshow(K3_1),title('7*7的维纳滤波处理(高斯噪声)结果');
subplot(3,4,8),imshow(K3_2),title('7*7的维纳滤波处理(椒盐噪声)结果');
subplot(3,4,9),imshow(K4_1),title('8*8的维纳滤波处理(高斯噪声)结果');
subplot(3,4,10),imshow(K4_2),title('8*8的维纳滤波处理(椒盐噪声)结果');
subplot(3,4,11),imshow(K5_1),title('9*9的维纳滤波处理(高斯噪声)结果');
subplot(3,4,12),imshow(K5_2),title('9*9的维纳滤波处理(椒盐噪声)结果');
K1_1=medfilt2(I1,[3,3]);
K1_2=medfilt2(I2,[3,3]);
K2_1=medfilt2(I1,[5,5]);
K2_2=medfilt2(I2,[5,5]);
K3_1=medfilt2(I1,[7,7]);
K3_2=medfilt2(I2,[7,7]);
K4_1=medfilt2(I1,[8,8]);
K4_2=medfilt2(I2,[8,8]);
K5_1=medfilt2(I1,[9,9]);
K5_2=medfilt2(I2,[9,9]);
figure,subplot(3,4,1),imshow(I1),title('pout图像加入高斯噪声');
subplot(3,4,2),imshow(I2),title('pout图像加入椒盐噪声');
subplot(3,4,3),imshow(K1_1),title('3*3的中值滤波处理(高斯噪声)结果');
subplot(3,4,4),imshow(K1_2),title('3*3的中值滤波处理(椒盐噪声)结果');
subplot(3,4,5),imshow(K2_1),title('5*5的中值滤波处理(高斯噪声)结果');
subplot(3,4,6),imshow(K2_2),title('5*5的中值滤波处理(椒盐噪声)结果');
subplot(3,4,7),imshow(K3_1),title('7*7的中值滤波处理(高斯噪声)结果');
subplot(3,4,8),imshow(K3_2),title('7*7的中值滤波处理(椒盐噪声)结果');
subplot(3,4,9),imshow(K4_1),title('8*8的中值滤波处理(高斯噪声)结果');
subplot(3,4,10),imshow(K4_2),title('8*8的中值滤波处理(椒盐噪声)结果');
subplot(3,4,11),imshow(K5_1),title('9*9的中值滤波处理(高斯噪声)结果');
subplot(3,4,12),imshow(K5_2),title('9*9的中值滤波处理(椒盐噪声)结果');

图1.3.4-1 pout原图

图1.3.4-2 pout图像均值滤波处理

图1.3.4-3 pout图像高斯滤波处理

图1.3.4-4 pout图像维纳滤波处理

图1.3.4-5 pout图像中值滤波处理
分析:由于对不同的图像所进行的操作及原理是一样的,所以在这里我只选用了一张图片进行实验,以减少不必要的篇幅。具体的分析在上面实现各个滤波器时候已经介绍,对于同一种滤波器来说,不同的模板大小的降噪效果差异较大,当模板选取过小时,去噪效果不明显,当模板选取过大时候,又会造成图片过模糊,特别是均值滤波,当模板大小为9*9时候,可以看到图片已经变得很模糊,这和其特性有关。
对于不同的滤波器,其降噪效果也存在较明显的区别,特别是应对不同的噪声,均值滤波器对椒盐噪声的消除效果是很好,对高斯噪声的消除效果则一般,因为无论怎么消除,其最终还是将噪声平均到了图像上。对于高斯滤波,当模板大小为5*5时候,可以看到其对高斯噪声的消除效果较好,但是对于椒盐噪声其作用效果甚微。对于维纳滤波,由于其采用了方差最小化,对于高斯噪声其消除效果也较好,但是对于椒盐噪声的消除还是能明显看到残余噪声,但是当模板增大后噪声消除的效果就很好了。中值滤波是一种非线性的方法,其能有效消除一些离散的噪声,比如椒盐噪声,但是对于高斯噪声其消除效果则一般。
**尝试不使用matlab函数,实现高斯滤波器或者中值滤波器,与 matlab自带函数进行对比,并分析差异 **
相关的实现过程在第(2)第(3)小点已实现,对于高斯滤波器,matlab自带的函数在不填写相关参数情况下默认模板大小为3*3,标准差为0.5,自编程实现则需要标明这两个参数。对于中值滤波器,matlab自带的函数medfilt2只能处理二维的中值滤波,而自编程实现中值滤波不仅可以处理二维输入,还能处理三维输入(见下图1.3.5-1)

图1.3.5-1 自编程中值滤波处理三维输入
版权归原作者 赵四司机 所有, 如有侵权,请联系我们删除。