0
0

浅谈VMD---变分模态分解

很多场景下，我们需要将信号进行分解，为我们下一步操作提供方便，常用的分解方法可以有EMD族类，例如EMD、EEMD、FEEMD、CEEMDAN、ICEEMDAN等，当然也有小波分解、经验小波分解等，总之分解方式多种多样，根据样本的特点，选用不同的分解方式。这里简要介绍VMD分解。

  1.  Konstantin等人在2014年提出了一个完全非递归的变分模态分解（VMD）它可以实现分解模态的同时提取。该模型寻找一组模态和它们各自的中心频率，以便这些模态共同再现输入信号，同时每个模态在解调到基带后都是平滑的。算法的本质是将经典的维纳滤波器推广到多个自适应波段，使得其具有坚实的理论基础，并且容易理解。采用交替方向乘子法对变分模型进行有效优化，使得模型对采样噪声的鲁棒性更强。

VMD分解的具体过程可以理解为变分问题的最优解，可以相应转化为变分问题的构造和求解。

以上就是VMD（变分模态分解）的理论部分，大家不一定全弄明白，因为本人看了原文，也不能完全弄懂里面的数学关系。大体知道分解的过程包含哪几个步骤即可，知网上面关于这类分解的文章也很多，大家可以参考浏览学习下。

下面直接上代码。

  1. function [u, u_hat, omega] = VMD(signal, alpha, tau, K, DC, init, tol)
  2. % Variational Mode Decomposition
  3. % Authors: Konstantin Dragomiretskiy and Dominique Zosso
  4. % zosso@math.ucla.edu --- http://www.math.ucla.edu/~zosso
  5. % Initial release 2013-12-12 (c) 2013
  6. %
  7. % Input and Parameters:
  8. % ---------------------
  9. % signal  - the time domain signal (1D) to be decomposed
  10. % alpha   - the balancing parameter of the data-fidelity constraint
  11. % tau     - time-step of the dual ascent ( pick 0 for noise-slack )
  12. % K       - the number of modes to be recovered
  13. % DC      - true if the first mode is put and kept at DC (0-freq)
  14. % init    - 0 = all omegas start at 0
  15. %                    1 = all omegas start uniformly distributed
  16. %                    2 = all omegas initialized randomly
  17. % tol     - tolerance of convergence criterion; typically around 1e-6
  18. %
  19. % Output:
  20. % -------
  21. % u       - the collection of decomposed modes
  22. % u_hat   - spectra of the modes
  23. % omega   - estimated mode center-frequencies
  24. %
  25. % When using this code, please do cite our paper:
  26. % -----------------------------------------------
  27. % K. Dragomiretskiy, D. Zosso, Variational Mode Decomposition, IEEE Trans.
  28. % on Signal Processing (in press)
  29. % please check here for update reference: 
  30. %          http://dx.doi.org/10.1109/TSP.2013.2288675
  32. %---------- Preparations
  34. % Period and sampling frequency of input signal
  35. save_T = length(signal);
  36. fs = 1/save_T;
  38. % extend the signal by mirroring
  39. T = save_T;
  40. f_mirror(1:T/2) = signal(T/2:-1:1);
  41. f_mirror(T/2+1:3*T/2) = signal;
  42. f_mirror(3*T/2+1:2*T) = signal(T:-1:T/2+1);
  43. f = f_mirror;
  45. % Time Domain 0 to T (of mirrored signal)
  46. T = length(f);
  47. t = (1:T)/T;
  49. % Spectral Domain discretization
  50. freqs = t-0.5-1/T;
  52. % Maximum number of iterations (if not converged yet, then it won't anyway)
  53. N = 500;
  55. % For future generalizations: individual alpha for each mode
  56. Alpha = alpha*ones(1,K);
  58. % Construct and center f_hat
  59. f_hat = fftshift((fft(f)));
  60. f_hat_plus = f_hat;
  61. f_hat_plus(1:T/2) = 0;
  63. % matrix keeping track of every iterant // could be discarded for mem
  64. u_hat_plus = zeros(N, length(freqs), K);
  66. % Initialization of omega_k
  67. omega_plus = zeros(N, K);
  68. switch init
  69.     case 1
  70.         for i = 1:K
  71.             omega_plus(1,i) = (0.5/K)*(i-1);
  72.         end
  73.     case 2
  74.         omega_plus(1,:) = sort(exp(log(fs) + (log(0.5)-log(fs))*rand(1,K)));
  75.     otherwise
  76.         omega_plus(1,:) = 0;
  77. end
  79. % if DC mode imposed, set its omega to 0
  80. if DC
  81.     omega_plus(1,1) = 0;
  82. end
  84. % start with empty dual variables
  85. lambda_hat = zeros(N, length(freqs));
  87. % other inits
  88. uDiff = tol+eps; % update step
  89. n = 1; % loop counter
  90. sum_uk = 0; % accumulator
  92. % ----------- Main loop for iterative updates
  94. while ( uDiff > tol &&  n < N ) % not converged and below iterations limit
  95.     
  96.     % update first mode accumulator
  97.     k = 1;
  98.     sum_uk = u_hat_plus(n,:,K) + sum_uk - u_hat_plus(n,:,1);
  99.     
  100.     % update spectrum of first mode through Wiener filter of residuals
  101.     u_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);
  102.     
  103.     % update first omega if not held at 0
  104.     if ~DC
  105.         omega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);
  106.     end
  107.     
  108.     % update of any other mode
  109.     for k=2:K
  110.         
  111.         % accumulator
  112.         sum_uk = u_hat_plus(n+1,:,k-1) + sum_uk - u_hat_plus(n,:,k);
  113.         
  114.         % mode spectrum
  115.         u_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);
  116.         
  117.         % center frequencies
  118.         omega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);
  119.         
  120.     end
  121.     
  122.     % Dual ascent
  123.     lambda_hat(n+1,:) = lambda_hat(n,:) + tau*(sum(u_hat_plus(n+1,:,:),3) - f_hat_plus);
  124.     
  125.     % loop counter
  126.     n = n+1;
  127.     
  128.     % converged yet?
  129.     uDiff = eps;
  130.     for i=1:K
  131.         uDiff = uDiff + 1/T*(u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i))*conj((u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i)))';
  132.     end
  133.     uDiff = abs(uDiff);
  134.     
  135. end
  137. %------ Postprocessing and cleanup
  139. % discard empty space if converged early
  140. N = min(N,n);
  141. omega = omega_plus(1:N,:);
  143. % Signal reconstruction
  144. u_hat = zeros(T, K);
  145. u_hat((T/2+1):T,:) = squeeze(u_hat_plus(N,(T/2+1):T,:));
  146. u_hat((T/2+1):-1:2,:) = squeeze(conj(u_hat_plus(N,(T/2+1):T,:)));
  147. u_hat(1,:) = conj(u_hat(end,:));
  149. u = zeros(K,length(t));
  151. for k = 1:K
  152.     u(k,:)=real(ifft(ifftshift(u_hat(:,k))));
  153. end
  155. % remove mirror part
  156. u = u(:,T/4+1:3*T/4);
  158. % recompute spectrum
  159. clear u_hat;
  160. for k = 1:K
  161.     u_hat(:,k)=fftshift(fft(u(k,:)))';
  162. end
  164. end

代码很长，尽量看，能看懂多少看懂多少。这里不再讲解，因为这里都是对数学原理的复现，如果要弄懂原理，建议比照原文和代码相结合，逐行去看。如果只是利用这种分解方式，关心得出的结果，那么就没有必要大费周章了。

  1. function [u, u_hat, omega] = VMD(signal, alpha, tau, K, DC, init, tol)

函数的输入输出，这里要解释一下。

函数的输入部分：signal代表输入信号，alpha表示数据保真度约束的平衡参数 ，tau表示时间步长，K表示分解层数，DC表示如果将第一模式置于DC(0频率)，则为true。 init表示信号的初始化，tol表示收敛容错准则。通常除了K，也就是分解模态数之外，其他参数都有相应的经验值。绝大部分文献对VMD的探索也是对分解模态数的确定，顶多再加上tau的讨论。（博主后面的文章中也会进行相应的讨论。）

函数的输出部分：u表示分解模式的集合，u_hat表示模式的光谱范围，omega 表示估计模态的中心频率。

下面是调用VMD分解的主程序。主要步骤就是输入信号值，确定VMD的分解参数，画图。

  1. tic
  2. clc
  3. clear all
  5. load('IMF1_7.mat')
  6. x=IMF1_7;
  7. t=1:length(IMF1_7);
  9. %--------- 对于VMD参数进行设置---------------
  10. alpha = 2000;       % moderate bandwidth constraint：适度的带宽约束/惩罚因子
  11. tau = 0.0244;          % noise-tolerance (no strict fidelity enforcement)：噪声容限（没有严格的保真度执行）
  12. K = 7;              % modes：分解的模态数
  13. DC = 0;             % no DC part imposed：无直流部分
  14. init = 1;           % initialize omegas uniformly  ：omegas的均匀初始化
  15. tol = 1e-6 ;        
  16. %--------------- Run actual VMD code:数据进行vmd分解---------------------------
  17. [u, u_hat, omega] = VMD(x, alpha, tau, K, DC, init, tol);
  18. figure;
  19. imfn=u;
  20. n=size(imfn,1); %size(X,1),返回矩阵X的行数；size(X,2),返回矩阵X的列数；N=size(X,2)，就是把矩阵X的列数赋值给N
  22. for n1=1:n
  23.     subplot(n,1,n1);
  24.     plot(t,u(n1,:));%输出IMF分量，a(:,n)则表示矩阵a的第n列元素，u(n1,:)表示矩阵u的n1行元素
  25.     ylabel(['IMF' ,int2str(n1)],'fontsize',11);%int2str(i)是将数值i四舍五入后转变成字符，y轴命名
  26. end
  27.  xlabel('样本序列','fontsize',14,'fontname','宋体');
  29. %时间\itt/s
  30.  toc;
  31.

下图记为分解的结果。

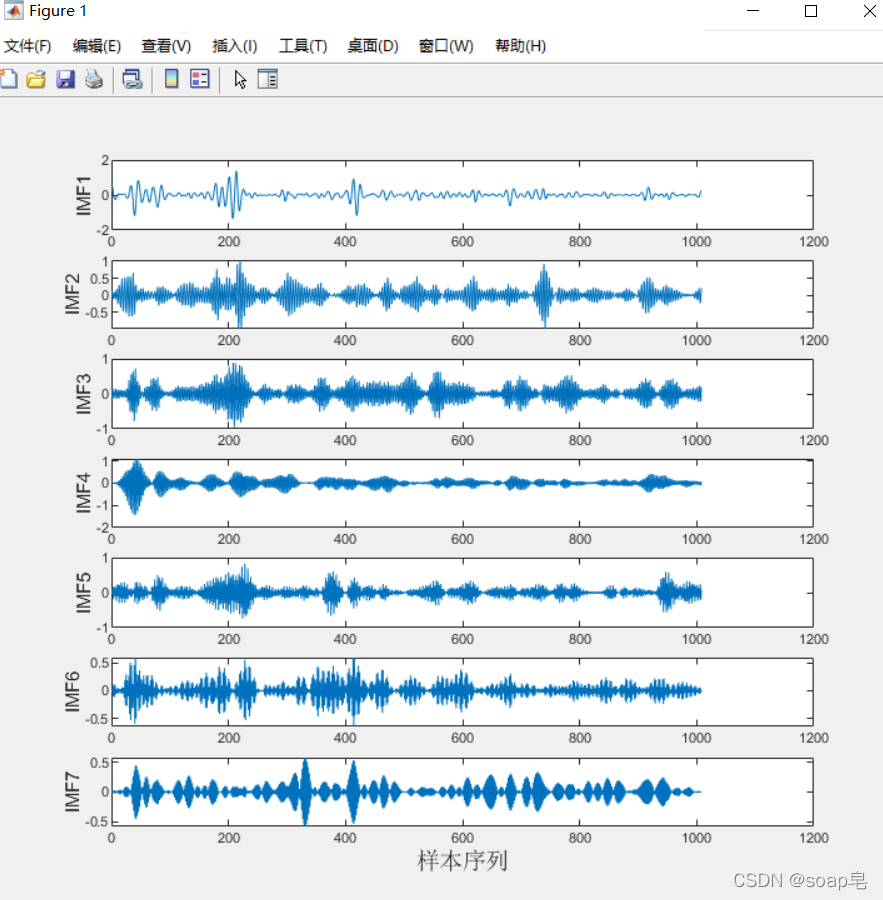
以上就是对VMD分解的简单描述，下面的博文中将探讨如何对分解层数进行相应固定。

标签： 人工智能 matlab 信号处理
本文转载自: https://blog.csdn.net/weixin_46062179/article/details/122268070
版权归原作者 soap皂 所有， 如有侵权，请联系我们删除。
登录后发布评论

“浅谈VMD---变分模态分解”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

网络安全法-网络运行安全

使用selenium/drissionpage时如何阻止chrome自动跳转http到https

docker desktop 里部署的Open WebUI 管理员密码忘记了的处理方法

在ubuntu20.04中搭建onsite比赛运行环境

利用开源的低代码表单设计器FcDesigner高效管理和渲染复杂表单结构

Kafka学习笔记

【前端】浏览器输入url到页面呈现发生了什么？

文章导航
没有找到文章内容分段。。。