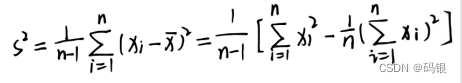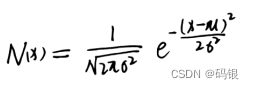数据挖掘(2.2)--数据预处理

二、数据描述

描述数据的方法,包括描述数据中心趋势的方法如均值、中位数，描述数据的分散程度的方法如方差、标准差,以及数据的其他描述方法如散点图和参数化方法等。

1.描述数据中心趋势

1.1平均值和截断均值

平均值(Mean),又称为均值或算数均值(Arithmeticmean),其计算方式如下:

例如.对于下列学生成绩列表,其算数均值为73.5分,即平均分是73.5分。可以看出，学生的成绩分布大体在平均值附近。
76,89,76,70,70,84,90,84,83,83

截断均值(Trimmed mean),即不考虑离群值,用其他值计算平均值。
如果其中一个同学因某种原因导致成绩太低，为了处理这种情况，可以使用截断均值。使用截断均值来进行计算，如：去除第一个同学的分数,余下9个同学算出分数平均值这比较符合直观印象。在许多比赛环节中,为了避免评委个人的偏好与偏向对整体评分造成影响,通常使用去掉个最低分,去掉一个最高分,用其他分数计算平均分的手段来进行打分,这就是一种形式的截断均值。

1.2加权平均值

加权算术均值( Weighted arithmetic mean)：不希望将所有的数据等同看待,而是希望让一些数据比另一些数据更有代表性,其计算方式如下:

如：比赛打分

评委：80，80，80，80，80

观众：30，40，50，60，50，40，30，20，10，40

希望评委的权重是观众的10倍

评委分数之和10+观众分数之和/评委人数10+观众人数

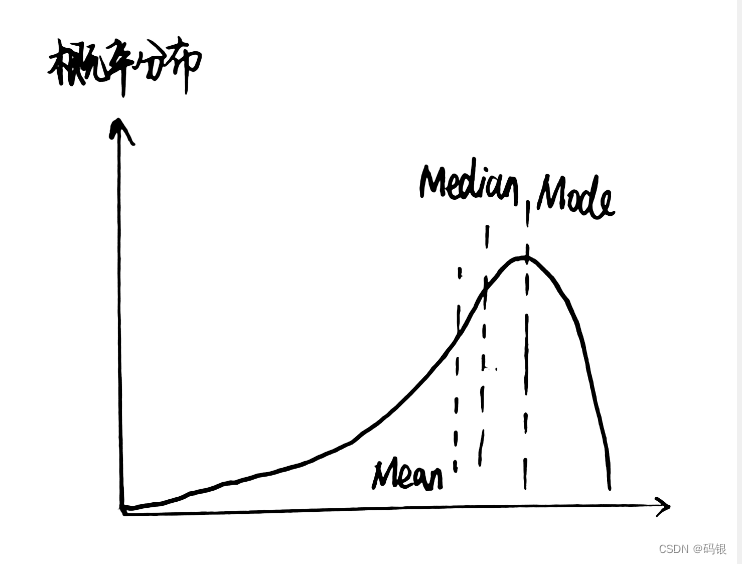
1.3中位数（Median）和众数(Mode)

众数、中位数和均值如图所示,对于仅有一个峰值的分布来说,三者之间的关系可以用一个经验公式来描述:

Mean一Mode= 3*(Mean一Median)
该公式并不一定总是成立,但是可以在一定程度上反映三者之间的关系。

2.描述数据的分散程度

希望数据之间相差很大,还是相差较小,这就是数据的分散程度。
衡量数据的分散程度的一个很好的指标是分位数,a分位数是从负无穷到某一点概率密度函数的积分(分布列求和)为a时那一点的值。比较常用的分位数为最小值(可以认为是0分位数)、0.25分位数(Q1)、中位数(0.5分位数，Q2)、0.75分位数(Q3)和最大值(可以认为是1分位数)。

2.1箱线图

通过这些分位数可以定义一些描述数据分散度的指标。范围是最大值与最小值之差，它描述了数据分布在多大的范围中;中间四分位数极差(IQR)是Q3-Q1，它反映了数据中心部分的分散程度;五数概要是上述5个分位数的整体,通常被用在箱线图中,用于形象表示数据的范围。

在箱线图中,有些数据点由于过于脱离整体,通常希望把它们单独表示出来，这些点称为离群点
(Outlier)。通常使用点与最近的中间四分位数的差来判断是否属于离群点，通常使用一一个常数k(经验值为1.5)与中间四分位数极差的成绩来定义这个临界差值。即当数据不属于以下区间时,认为数据为离群点:
[Q1 - k(Q3 - Q1),Q3 +k(Q3 - Q1)]

2.2方差和标准差

衡量数据分散程度的另外两个常用的指标是方差和标准差。方差通常用S2表示，是数据的平方误差的期望,样本的(无偏)方差的计算公式为:

标准差通常用s表示,标准差是方差的均方根值。正态分布是一种典型的概率分布,其概率密度函数可以使用均值μ和标准差σ两个参数来表示:

2.3正态分布

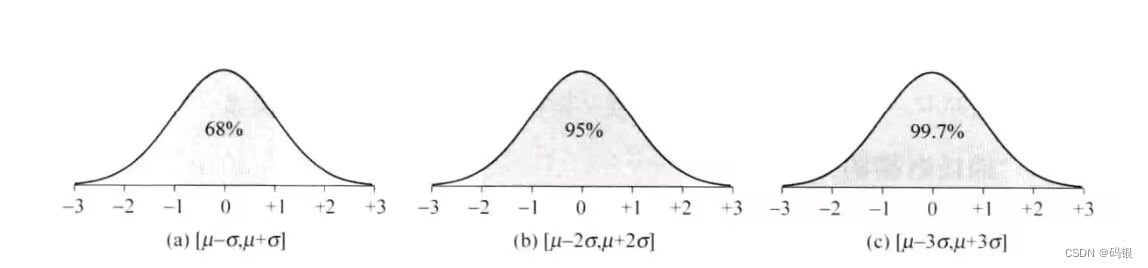
正态分布是分布比较集中的单峰分布,其主要的概率集中在均值附近,其中,[μ- - σ.p+a]集中了68%的概率,[μ- 2σ,p+2σ]集中了95%的概率,[μ- 3σ,p+ 3o]集中了99. 7%的概率。正态分布的概率分布如图所示。

3.数据清洗

数据清洗中进行的任务包括填补数据中的缺失值，识别数据中的离群点,对有噪声数据进行平滑等。数据清洗在提升数据质量方面具有相当大的作用。

3.1数据缺失的处理

数据缺失可能由各种原因导致

采集设备的故障可能会造成空白数据，一个属性可能与其他属性产生冲突而造成它被删除,数据在录入阶段可能出现误解而未能录人,在数据录入的时刻可能某个属性并不受重视而未被采集,采集数据的需求可能发生了变化造成数据属性集合的变化。

处理缺失数据

最简单的处理方法是当数据的某个属性缺失时,丢弃掉整条数据记录。
人工填补缺失值,即对于某些缺失的属性,用人工的方式进行填补。人工填补的前提是数据存在一定的冗余,其缺失属性可以通过其他属性进行推断。
对于缺失数据采用较多的处理方式是自动对缺失值进行填补。自动填补数据的最简单办法是对某个属性字段,对所有缺失该属性的数据填补统一的值。

3.2数据清洗

数据噪声是指数据中存在的随机性错误和偏差,许多原因可能导致这些错误与偏差。
其中，数据采集中一些客观因素的制约带来了数据噪声。数据采集设备可能具有缺陷和技
术限制。

在数据挖掘领域中,为了保证数据预处理工作的高效,为了处理噪声数据,通常用到的方法是分箱、聚类分析和回归分析等，有时也会将计算机判决与人的主观判断相结合。
数据清洗的过程通常是由两个过程的交替迭代组成数据异常的发现和数据的清洗。对于数据首先需要进行审查,根据先验知识如数据的取值范围、数据依赖性、数据的分布、数据的唯一性、连续性和空/非空性质等,可以发现数据中存在的异常现象。在发现数据异常后,使用数据清洗方法对数据进行转换。数据转换可以使用专门的数据迁移工具进行，通常称为ETL( Extract, Transform，Load)工具。