余弦相似度

一、余弦相似度的定义

余弦相似度算法：一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小，余弦值接近1，夹角趋于0，表明两个向量越相似，余弦值接近于0，夹角趋于90度，表明两个向量越不相似。

二、余弦相似度的公式

回顾一下函数的概念，我们就会发现 $\delta$ 是 $a, b, c$ 三个变量的函数。对于同样一个角，如果三角形边长都比较长，那么 $\delta$ 的动态范围很大；如果边长很短， $\delta$ 的动态范围就很小。为了消除边长的影响，我们将 $\delta$ 除以夹角的两个边的长度 $a$ 和 $b$ ，写成

$\delta=\frac{a^2+b^2-c^2}{2ab}$

可以证明，这样计算出的 $\delta$ 的动态范围就在 $-1$ 和 $+1$ 之间。如果 $\delta=-1$ ，那么夹角最大，就是180°；如果 $\delta=0$ ，就是90°；如果 $\delta=1$ ，就是0°角。事实上 $\delta$ 就等于夹角的余弦函数值。这样一来，我们就从勾股定理出发，建立了角度判定因子 $\delta$ 和具体角度之间的关系，这种关系就是余弦定理。通常余弦定理用下面的公式来表述：

$cosC=\frac{a^2+b^2-c^2}{2ab}$ 或者 $c^2=a^2+b^2-2ab cosC$

有了余弦定理后, 我们会发现勾股定理其实是余弦定理在直角情况下的特例。当然，换一个角度来看,余弦定理是勾股定理的扩展。

有了余弦定理,我们就能够通过三角形的三条边的边长,计算它的任意一个内角。对于两个向量来讲,如果我们把它们的起点放到原点,那么原点和这两个向量终点构成一个三角形。

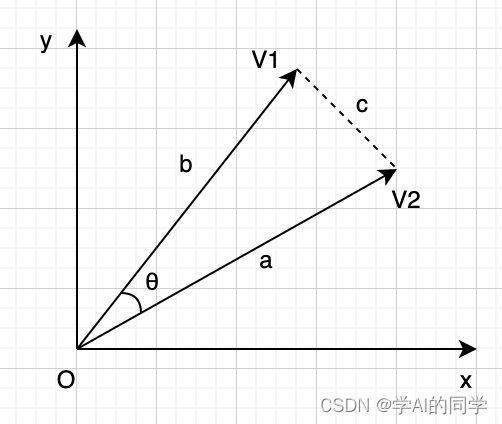
由两个已知的向量 $V_1$ 和 $V_2$ ，利用余弦定理计算它们的夹角θ

这个三角形的三条边显然是确定的,由此我们可以用余弦定理公式算出两个向量的夹角θ。

值得一提的是， $a^2+b^2-c^2$ 恰好等于a和b两个向量的点积<a,b>的两倍，我们将它带入余弦定理公式就能得到

$cosC=\frac{<a,b>}{||a||.||b||}$

这个公式被看做余弦定理的另一种表述方式,它的推导过程也是比较好理解的

由于 c²=(a-b)²=(b-a)²

所以 (a-b)²=b²+a²-2||a||.||b|| cosC

      a²-2ab+b²=b²+a²-2||a||.||b|| cosC
      -2ab=-2 ||a||.||b|| cosC
     <a,b>=||a||.||b||cosC
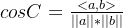
   ![cosC=\frac{<a,b>}{||a||*||b||}](https://latex.csdn.net/eq?cosC%3D%5Cfrac%7B%3Ca%2Cb%3E%7D%7B%7C%7Ca%7C%7C*%7C%7Cb%7C%7C%7D)

$<a,b>$ 表示向量的点积，其中向量范数$ $||a||=\sqrt{a_1^2+a_2^2+...+a_n^2}$

对于多维向量 $V_1=(v_{1,1},v_{1,2},...v_{1,n})$ 和 $V_2=(v_{2,1},v_{2,2},...,v_{2,n})$ 的点积，通常使用下面的公式计算： $V_1.V_2=v_{1,1}v_{2,1}+v_{1,2}v_{2,2}+...+v_{1,n}v_{2,n}$

标签：人工智能机器学习自然语言处理

本文转载自: https://blog.csdn.net/m0_71145378/article/details/126910793
版权归原作者 学AI的同学 所有，如有侵权，请联系我们删除。

一、余弦相似度的定义

二、余弦相似度的公式

发表评论

“余弦相似度”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航