多元时间序列分析统计学基础：基本概念、VMA、VAR和VARMA

多元时间序列是一个在大学课程中经常未被提及的话题。但是现实世界的数据通常具有多个维度，所以需要多元时间序列分析技术。在这文章我们将通过可视化和Python实现来学习多元时间序列概念。这里假设读者已经了解单变量时间序列分析。

1、什么是多元时间序列？

顾名思义，多元时间序列是与时间相关的多维数据。我们可以用以下数学公式定义多元时间序列数据：

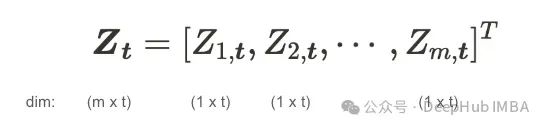
其中Zᵢ,ₜ是时间t下第i个分量变量，注意它对每个i和t都是一个随机变量。Zₜ具有(m, t)维度。当我们分析多元时间序列时，不能应用标准的统计理论。这意味着什么？请记住多元线性回归。

当计算多元线性回归(1)的似然时，我们假设样本中的每个观测值(=xᵢ)独立于其他观测值。因此可以通过单个观测值的概率密度的乘积轻松计算似然。通常假设观测值遵循具有以下参数的正态分布。

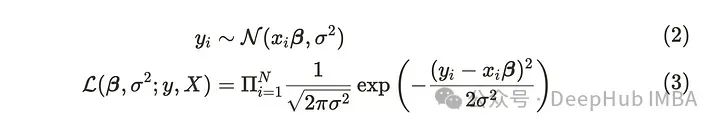
但是在多元时间序列中，Zₜ依赖于i和t。因此不能应用与多元线性回归相同的假设。为了分析多元时间序列，我们需要了解一些基本概念。

平稳性

在单变量时间序列中，当时间序列在时间上具有相同的均值和方差，并且协方差取决于时间滞后时，它具有弱平稳性。同理m维多元时间序列也具有平稳性，如果每个分量序列都是弱平稳的，并且其均值和方差不随时间变化。如下图所示

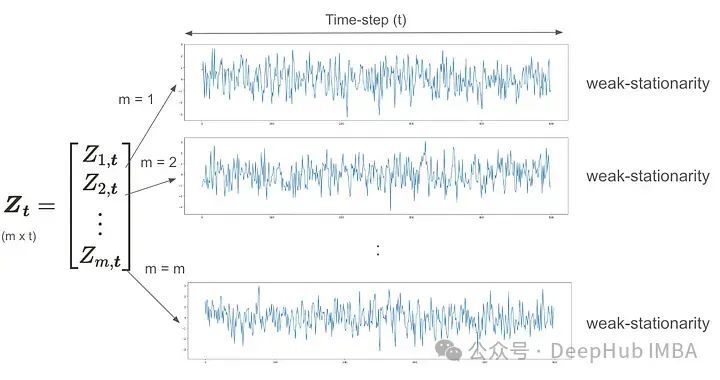
协方差和相关矩阵

考虑平稳多元时间序列过程Zₜ的统计量。m维多元时间序列过程的均值可以写成：

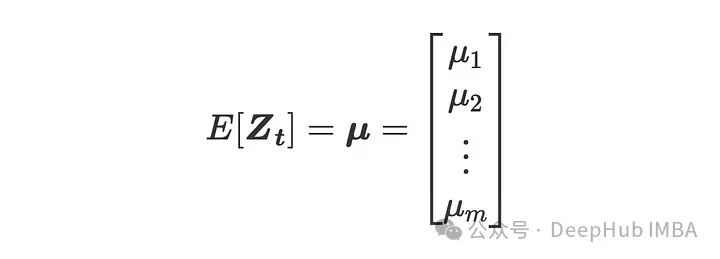
均值向量具有(m, 1)维度。滞后k协方差矩阵将如下所示：

证明如下：

当k = 0时，矩阵Γ(0)可以很容易地看作是其他变量之间的方差-协方差矩阵。当k > 0时，矩阵Γ(k)是单变量时间序列自协方差的扩展。不仅计算同一变量之间的自协方差，还计算一个变量与其他变量之间的自协方差。

对于相关矩阵，只需使用方差矩阵对协方差矩阵进行归一化。

其中D是对角矩阵，每个元素是第i个分量序列的方差。所以ρ(k)的第i个对角元素是第i个分量序列Zᵢ,ₜ的自相关函数，而ρ(k)的(i, j)非对角元素是分量序列Zᵢ,ₜ和Zⱼ,ₜ之间的互相关函数。

向量白噪声过程

如果m维向量过程aₜ具有以下参数，则称其为向量白噪声过程。

其中Σ是(m x m)对称协方差矩阵。它是单变量时间序列中白噪声的扩展。白噪声过程的分量在不同时间是不相关的，就像单变量白噪声过程一样。一个向量与其时间滞后向量之间的协方差变为零。这里白噪声过程的分量可能在同一时间点上相关。所以通常我们假设高斯白噪声，这意味着aₜ遵循多元高斯分布，可以将高斯白噪声称为VWN(0, Σ)。

以上就是多元时间序列的基本概念。下面我们将探讨代表性的向量时间序列过程，如VMA、VAR和VARMA。

2、向量移动平均过程(VMA)

向量移动平均(VMA)过程是移动平均(MA)过程的多维变量版本。让我们快速回顾一下MA过程。移动平均(MA)过程由当前和先前冲击Uₜ的总和组成。MA(q)过程可以用以下公式表示。

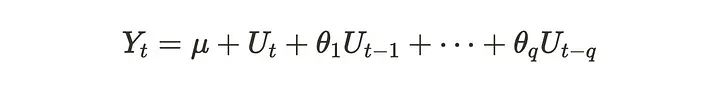
Uₜ在许多情况下被假定为白噪声。MA(q)过程具有由前q步冲击组成的时间序列{Yₜ}。这里MA(q)过程是弱平稳的，这意味着均值和方差是恒定的，协方差取决于时间滞后。当我们使用后移算子B时，可以重写公式如下：

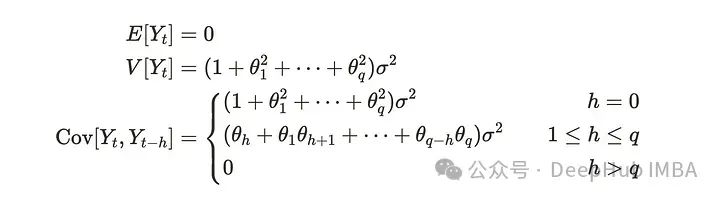
这样可以以有组织的方式重写它。许多教科书利用这种表达方式。MA(q)过程具有以下性质。

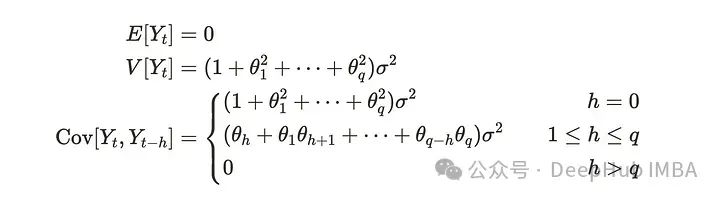
回到VMA的话题，它只是MA过程的向量形式(多元)版本！为了直观地理解VMA过程，我们考虑m维VMA(1)的例子。

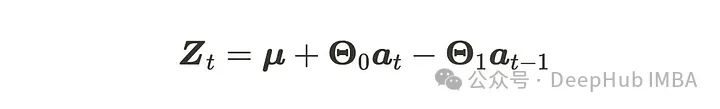
其中Zₜ、𝜇和aₜ具有(m, 1)维度，𝚯具有(m, m)维度。注意，𝚯₀是单位矩阵。aₜ是m维高斯白噪声过程VWN(0, Σ)的序列。VMA(1)过程具有以下性质。

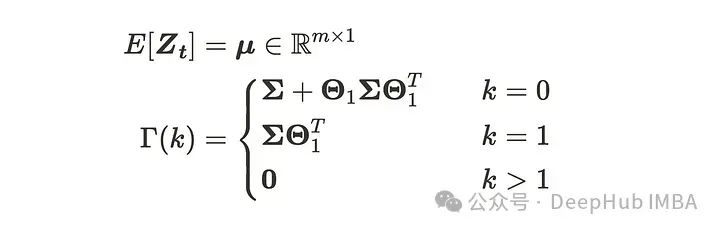
VMA(1)过程的均值始终为𝜇，因为它由均值为0的高斯白噪声的总和组成。而协方差矩阵看起来有点棘手。我们需要通过详细推导来解释。首先，𝛤(0)即等价于方差，可以推导如下：

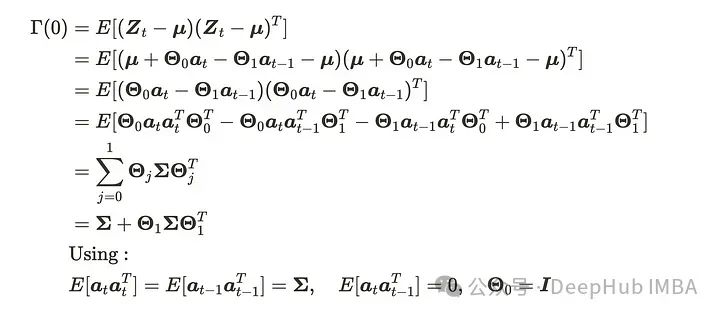
同样的程序可以用于计算以下内容。

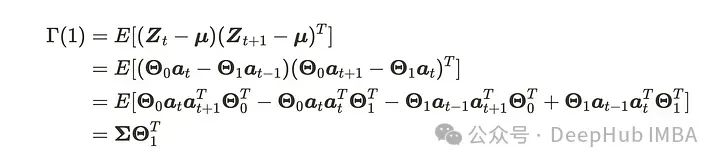
这里在𝛤(1)中包括𝛩的负号是为了方便。

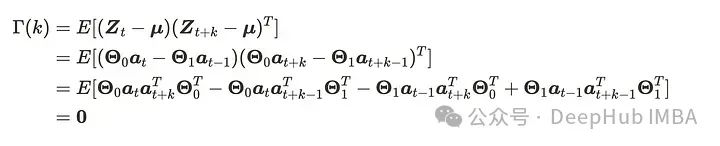
均值和自协方差几乎是类似的，但区别在于VMA具有MA过程参数的矩阵形式。这些公式看起来很复杂，所以我们通过可视化来检查具体的例子。我们假设我们有以下条件。

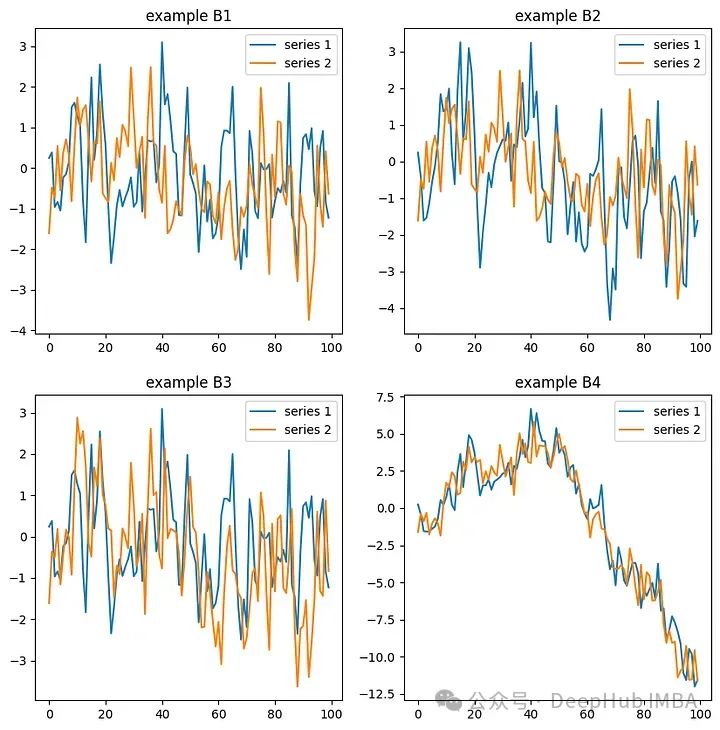
为简单起见，我们将均值向量设置为零。尝试四种系数案例(B1 ~ B4)。下图显示了每种系数案例的100个样本的结果。

在B1系数中，它们是独立的MA(1)过程。在B2和B3系数中，一个序列是独立的MA(1)过程，但另一个序列与独立的MA(1)过程之一相关。在B4系数案例中，两个序列都相互关联。VMA过程只是MA过程的多元版本，但由于有更多变量，我们必须考虑分量之间的相关性。

现在，让我们将话题扩展到VMA(q)过程。m维VMA(q)过程由以下公式给出：

![]

aₜ是m维高斯白噪声过程VWN(0, Σ)的序列。VMA(q)过程具有以下性质。

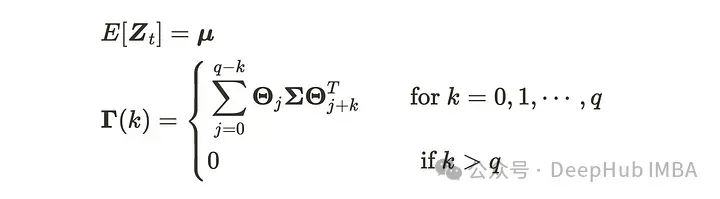
VMA(q)过程的均值始终为𝜇，因为VMA(q)由均值为0的VWN过程组成。我们还可以计算VMA(q)过程的协方差矩阵函数如下。

因此，VMA(q)过程无论如何都具有平稳性，协方差矩阵将在滞后q之后截断。与MA过程类似，我们可以使用相关矩阵或AIC来确定q的阶数。AIC在定义阶数时更方便，但请注意AIC需要计算所有阶数模式，因此需要大量计算。

在VMA部分的最后，有一个重要的概念叫可逆性。如果我们可以将VMA(q)过程写成如下的自回归表示，则称其为可逆的：

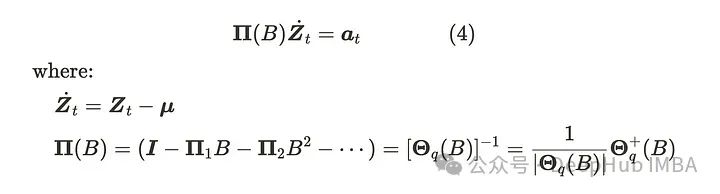
𝚯+(B)是伴随矩阵。我们可以推导方程(4)如下：

如果随机过程(Zₜ)是可逆的，它就有一个无限自回归表示(AR(∞))。如果行列式方程|𝚯q(B)| = 0的所有根满足单位圆外，则该序列是可逆的。

3、向量自回归过程(VAR)

向量自回归(VAR)过程是自回归(AR)过程的多维变量版本，类似于VMA过程。让我们快速回顾一下AR过程。自回归(AR)过程使用先前步骤的值来预测未来值。AR§过程可以用以下公式表示。

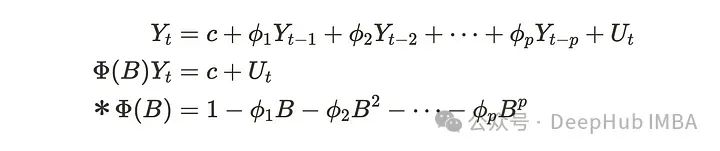
Uₜ被假定为白噪声。第二个方程使用后移算子来表示AR§过程。如果行列式方程|𝚽(B)| = 0的所有根的模满足单位圆外，则AR§过程是弱平稳的。

回到VAR的话题，它再次只是AR过程的向量形式(多元)版本！为了直观地理解VAR过程，让我们考虑m维VAR(1)的例子。

其中Zₜ和aₜ具有(m, 1)维度，𝚽具有(m, m)维度。aₜ是m维高斯白噪声过程VWN(0, Σ)的序列。第二个方程使用后移算子来表示VAR(1)方程。该模型是可逆的，因为它是VAR模型。如果行列式方程|I — 𝚽₁B| = 0的所有根位于单位圆外，则VAR(1)过程是平稳的。我们还可以将方程转换如下：

让我们通过可视化来检查具体的例子。假设有以下条件。

结果如下：

在B1系数中，它们是独立的AR(1)过程。同时在其他系数案例中，一个序列跟随另一个。最后一个案例是非平稳的。为确保时间序列适当平稳，需要计算公式(6)的特征值。结果如下所示。

 # sample coefficients of VAR(1) process  
 B1 = np.array([[0.5, 0.0], [0.0, 0.5]])  
 B2 = np.array([[0.5, 0.5], [0.0, 0.5]])  
 B3 = np.array([[0.5, 0.0], [0.5, 0.5]])  
 B4 = np.array([[0.5, 0.5], [0.5, 0.5]])  
   
 # calculate the eigenvalue  
 for i, B in enumerate([B1, B2, B3, B4]):  
     X = np.eye(2) - B  
     w, v = np.linalg.eig(X)  
       
     print(w)

现在，可以验证B1、B2和B3是平稳的，但B4是非平稳的。也可以使用增广迪基-富勒检验来检查每个时间序列是否平稳，就像单变量时间序列一样。但请注意这不足以检查VAR过程的平稳性。

需要再次强调VAR过程只是AR过程的多元版本(就像VMA过程一样)，但由于有更多变量，我们必须考虑分量之间的相关性。

下面就可以将话题扩展到VAR§过程。m维VAR§过程由以下公式给出：

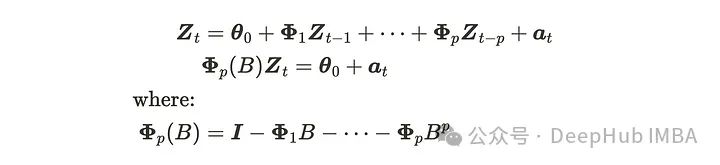
其中Zₜ和aₜ具有(m, 1)维度，𝚽具有(m, m)维度。aₜ是m维高斯白噪声过程VWN(0, Σ)的序列。由于AR§过程是可逆的，如果|Φₚ(B)| = 0的根位于单位圆外，则该过程是平稳的。这与AR§过程相同，但VAR§是向量化版本。

当AR§过程是平稳的，它具有以下均值和协方差。

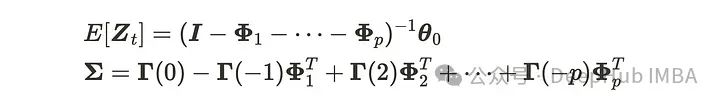
可以推导均值如下：

推导协方差比较棘手。首先需要推导𝛉值。

可以推导第二个方程，因为𝜇始终是常数。接下来需要转换VAR§方程。

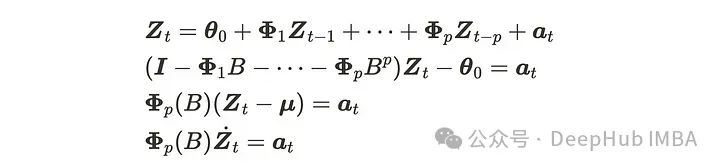
你是否已经看到类似最后一个方程的公式？在VMA部分已经看到过这个。如果VAR§过程是平稳的，它可以写成VMA表示。

然后协方差矩阵计算如下：

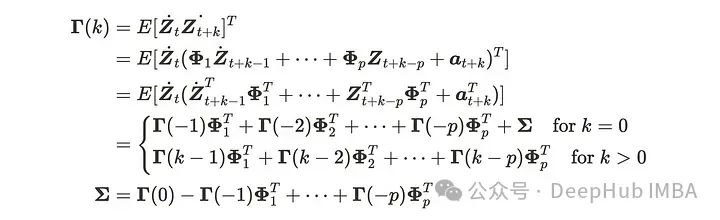
在公式中，它是由广义Yule-Walker矩阵方程推导出来的，我们不解释这个概念，总之就是如果VAR或VMA满足特定条件，它们可以相互转换。

与AR过程类似，可以利用偏相关矩阵来找到阶数。同样AIC也可以使用而且更方便。但是AIC需要计算所有阶数，因此需要大量计算。如果有很多变量并且似乎有很多滞后，使用相关矩阵仍然是一个好方法。

上面已经学习了VMA和VAR过程。在单变量时间序列中，有ARMA过程，它结合了AR和MA过程。我们也有多元时间序列的VARMA。

4、向量自回归移动平均过程(VARMA)

VARMA过程是VAR和VMA过程的组合。m维向量自回归移动平均(VARMA)过程具有阶数p和q，分别对应于VAR和VMA过程，可以描述为：

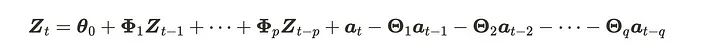
我们称之为VARMA(p, q)。可以重新表述这个方程如下：

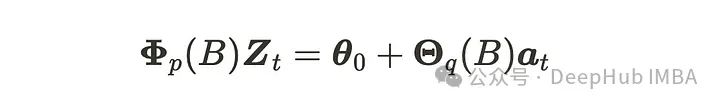
其中Zₜ和aₜ具有(m, 1)维度，𝚽和𝚯具有(m, m)维度。aₜ是m维高斯白噪声过程VWN(0, Σ)的序列。

由于VMA过程是平稳的，平稳性取决于VAR项。因此当|Φₚ(B)| = 0的根位于单位圆外时，VARMA过程是平稳的。可逆性取决于VMA项。如果行列式多项式|𝚯q(B)| = 0的所有根位于单位圆外，则VARMA过程是可逆的。

让我们回顾一下VMA、VAR和VARMA过程。它们具有与单变量时间序列类似的想法，但在多元时间序列中具有多维数据。因此，我们不仅需要考虑当前时间步和前一时间步之间的相关性，还需要考虑变量之间的相关性。这就是多元时间序列理论部分的结束。现在，让我们使用具体的例子来实现它们！

5、实际案例

最后我们将在Python中实现多元时间序列。使用美国月度零售销售收入数据。它包含五个行业，分别是AUT（汽车）、BUM（建筑材料）、GEM（一般商品）、COM（消费材料）和HOA（家用电器），从2009年6月到2016年11月，n = 90。每个时间序列数据看起来像这样：

很明显它们是非平稳的。因此需要试着对它们差分。

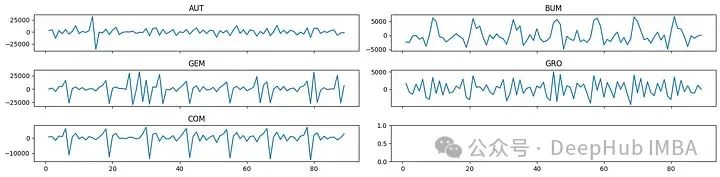
现在，情况稍好一些。但是似乎存在季节性，这是一种规则的、周期性的数据集变化，但为了简单起见，我们忽略它。该序列并不完全平稳，所以将使用VAR和VARMA模型。在Python中，可以使用statsmodels轻松实现VAR和VARMA建模

VAR建模

对于VAR建模，我们可以选择要计算的最大阶数，模型会根据给定的标准（如AIC）自动选择最佳模型。在以下例子中，我选择5作为最大滞后。

 var = sm.tsa.VAR(diff_df)
 result = var.fit(maxlags=5, ic='aic')
 result.summary()

可以看到最佳模型是五阶滞后模型。结果图如下。相关矩阵显示了变量之间的相关性，如COM和GRO。因此，它仍然不是平稳的。

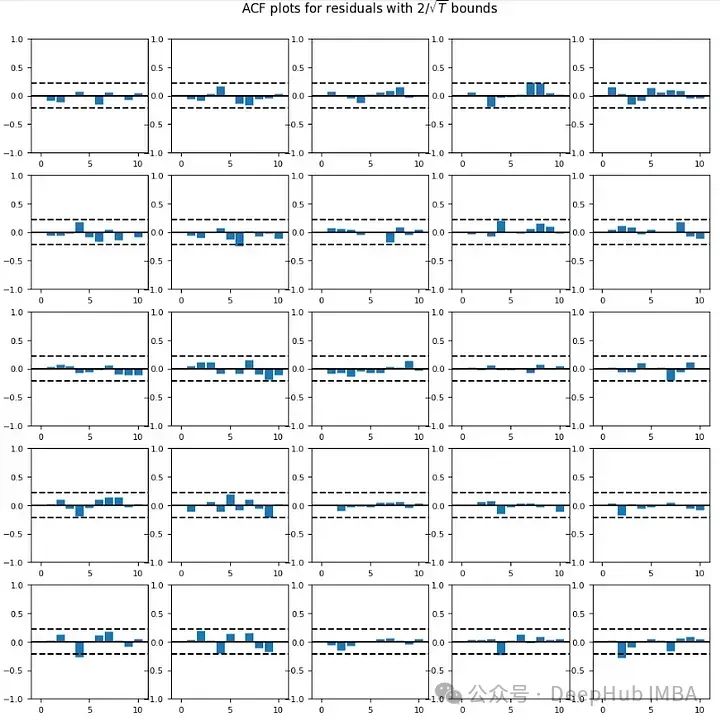
有一些相关性。因此通过调整参数，模型还有改进的空间。

VARMA建模

对于VARMA建模，没有内置的函数来为我们选择最佳顺序。所以需要遍历顺序的组合。

 # modeling
 results = pd.DataFrame(columns=['p', 'q', 'AIC'])
 
 for p in range(1, 5):
     for q in range(1, 5):
         model = sm.tsa.VARMAX(diff_df, order=(p, q))
         result = model.fit(maxiter=1000, disp=False)
         
         results = results.append({'p': p, 'q': q, 'AIC': result.aic})
         
 res_df = pd.DataFrame(results, columns=['p', 'q', 'AIC'])
 res_df.sort_values(by=['AIC']).head()

这需要几分钟才能完成。VARMA的计算往往是不稳定的，因此VAR模型在实践中更好。结果如下。

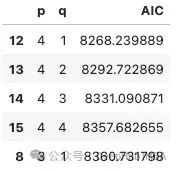
在这种情况下，VARMA(4,1)是最好的模型，它与VAR模型的阶数相同。从VAR和VARMA结果来看，q的阶数越小越好。如果我们想创建一个更合适的模型，则需要考虑季节性因素。比如说Meta的Prophet库对于构建模型似乎很方便，也是一个不错的选择，不过他的原理不在本文的讨论范文内，我们后面再讲。

https://avoid.overfit.cn/post/3fa1578d13664416b764babe25826adb

作者：Yuki Shizuya