一.C4.5算法的简介:
C4.5并不是单单一个算法而是一套算法,主要用于对机器学习和数据挖掘中的分类问题。它是一种有监督的学习,也就是说对于该算法我们需要先给它们提供一个数据集,这个数据集包含多个实例,每个实例都包含多个属性,该实例用这些属性描述,根据属性取值的不同被划分到不同的互斥类中。
C4.5算法就是从提供的数据集中学习到如何将不同属性值的实例划分到不同类的映射,当我们提供一套全新的属性值的时候,它能够通过学到的映射对新的属性进行分类。
C4.5是决策树算法的一种。决策树算法作为一种分类算法,目标就是将具有p维特征的n个样本分到c个类别中去。相当于做一个投影,c=f(n),将样本经过一种变换赋予一种类别标签。决策树为了达到这一目的,可以把分类的过程表示成一棵树,每次通过选择一个特征pi来进行分叉。
那么怎样选择分叉的特征呢?每一次分叉选择哪个特征对样本进行划分可以最快最准确的对样本分类呢?不同的决策树算法有着不同的特征选择方案。ID3用信息增益,C4.5用信息增益率,CART用gini系数。
下面主要针对C4.5算法,我们用一个例子来计算一下。
二.C4.5算法原理:
C4.5算法是一种经典的决策树学习算法,它是ID3算法的一种改进和优化。与ID3算法相比,C4.5算法具有以下几个改进:
- 用信息增益率代替信息增益作为选择划分属性的标准,解决了信息增益容易偏向取值比较多的属性的问题。
- 能够处理连续型属性数据,不需要对连续型属性进行离散化处理。
- 能够处理缺失属性值,利用缺失属性值的样本进行决策树的训练。
C4.5算法的基本思想是将数据集递归地划分为小的子集,直到子集中样本的所有特征属性均相同或无法继续划分为止。得到的决策树就是基于训练集构建的分类模型。
C4.5算法的具体步骤如下:
- 选择当前节点的最优划分属性,即使得信息增益率最大的属性,如果不存在则该节点为叶子节点。
- 对选择的最优属性的每个取值,分别构建一个子节点,并将样本点分配到这些子节点中。
- 对每个子节点,递归地执行步骤1-2,直至满足终止条件,即到达叶子节点或无法继续划分。
- 构建好决策树,用它进行测试数据的分类预测。
C4.5算法在构建决策树时,采用了自上而下递归的方法,每次选择最优划分属性进行划分,并在该属性的每个取值上递归地划分数据集。这样,就能得到一个覆盖了训练集所有样本的决策树模型,并可用来对新的测试样本进行分类预测。
三.C4.5案例分析:
例如,如图1,这组训练数据,属性值包括是否有房,婚姻状况,年收入,所有的实例被划分为两类,也就是 是否是拖欠贷款者。我们的目的就是从训练数据中学到一个映射,这个映射可以用于对于在图中未出现的实例属性取值情况进行有效分类。
也就是说,假如有一个有房、单身、年收入为50X的人(图中未出现),推测出这个人是否是拖欠贷款者

Figure 1
3.1决策树构建:
a.将所有训练数据集放在根节点上;
b.遍历每种属性的每种分割方式,找到最好的分割点;
c.根据2中找出的最好分割点将根节点分割成多个子节点(>=2);
d.对剩下的样本和属性重复执行步骤2/3,直到每个节点中的数据都属于同一类为止。
C4.5算法是采用信息增益率来进行节点的分裂
注意:C4.5算法并不直接选择增益率最大的候选划分属性,而是使用了一个启发式:
先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
3.2信息增益率:
增益率是用前面的信息增益Gain(D, a)和属性a对应的"固有值"(intrinsic value)的比值来共同定义的。属性 a 的可能取值数目越多(即 V 越大),则 IV(a) 的值通常会越大。
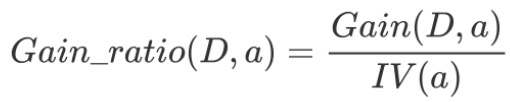
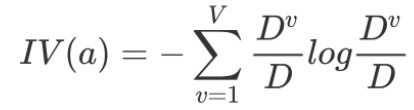
3.3计算
根据是否有房、婚姻状况、年收入三个属性来判断类别标签拖欠贷款者(是、否)
对于离散属性的处理:(有无房、婚姻状况)
a.计算类别信息熵
** **类别信息熵表示的是所有样本中各种类别出现的不确定性之和。根据熵的概念,熵越大,不确定性就越大,把事情搞清楚所需要的信息量就越多。
总体信息熵样本10个,是拖欠贷款者有3个,不是拖欠贷款者有7个。
b.计算每个属性的信息熵
每个属性的信息熵相当于一种条件熵。他表示的是在某种属性的条件下,各种类别出现的不确定性之和。属性的信息熵越大,表示这个属性中拥有的样本类别越不“纯”
c.计算信息增益
信息增益的 = 熵 - 条件熵,在这里就是 类别信息熵 - 属性信息熵,它表示的是信息不确定性减少的程度。如果一个属性的信息增益越大,就表示用这个属性进行样本划分可以更好的减少划分后样本的不确定性,当然,选择该属性就可以更快更好地完成我们的分类目标。
d.计算属性分裂信息度量
用分裂信息度量来考虑某种属性进行分裂时分支的数量信息和尺寸信息,我们把这些信息称为属性的内在信息(instrisic information)。信息增益率用信息增益/内在信息,会导致属性的重要性随着内在信息的增大而减小(也就是说,如果这个属性本身不确定性就很大,那我就越不倾向于选取它),这样算是对单纯用信息增益有所补偿。
e.计算信息增益率
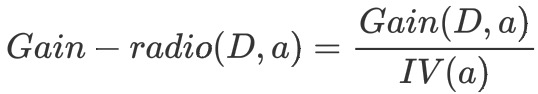
从属性中找出信息增益高于**平均水平的属性**,**再从中选择增益率最高的作为分割点**
对于连续性属性的处理:(年收入)
a.对年收入属性的各个值进行升序排序
b.选取分裂节点,对于连续性属性,它的分裂节点是任意相邻两个取值的中点,最后得到所有分裂点的信息熵,选择信息熵最小,即信息增益最大 的作为分裂点。
注意:这里用信息增益最大而不是信息增益率最大
最终得到所有属性的信息增益率,选取信息增益率最大的属性作为分裂属性,
若分裂之后,发现子结点都是“纯”的,因此子节点均为叶子节点,
选择“不纯“的结点继续分裂 重复以上步骤
下面解释一下子结点是“纯”的意思
子节点是纯的情况指的是一个节点的所有子节点都只包含同一类别的样本,此时就无需再进行划分而可以直接将该节点作为叶节点。
以C4.5算法生成决策树过程中包含连续数值属性的处理为例,假设我们的数据集中有以下数据:
ageincomestudentcredit ratingbuys computer31highnofairno23highyesexcellentyes36lownofairno28lownofairyes45mediumnofairyes
首先,我们需要将连续的数值属性转化为离散值。可以选择根据某个阈值来将其二元化,例如将年龄属性以 30 为阈值,将年收入属性以 high、medium 和 low 三个值进行离散化。 转换后的数据如下所示:
ageincomestudentcredit ratingbuys computer<=30highnofairno<=30highyesexcellentyes>30lownofairno>30lownofairyes>30mediumnofairyes
接下来,我们需要找到最佳属性进行划分。C4.5算法采用信息增益率作为划分属性的选择标准。在划分属性时,假设我们选择了年龄age属性作为划分属性,然后将它二元化为<=30和>30两个离散值。根据年龄属性划分的子节点数据如下:
- 子节点 1,年龄 <= 30:样本 2 个,均属于同一类别(不购买电脑),该子节点为纯节点。
- 子节点 2,年龄 > 30:样本 3 个,其中有 2 个属于同一类别(购买电脑),该子节点非纯。
显然,第一个子节点已经是一个纯节点,不需要再继续划分;而对于第二个子节点,我们需要对其进行进一步划分。
本题具体步骤如下(忽略潦草的字体):




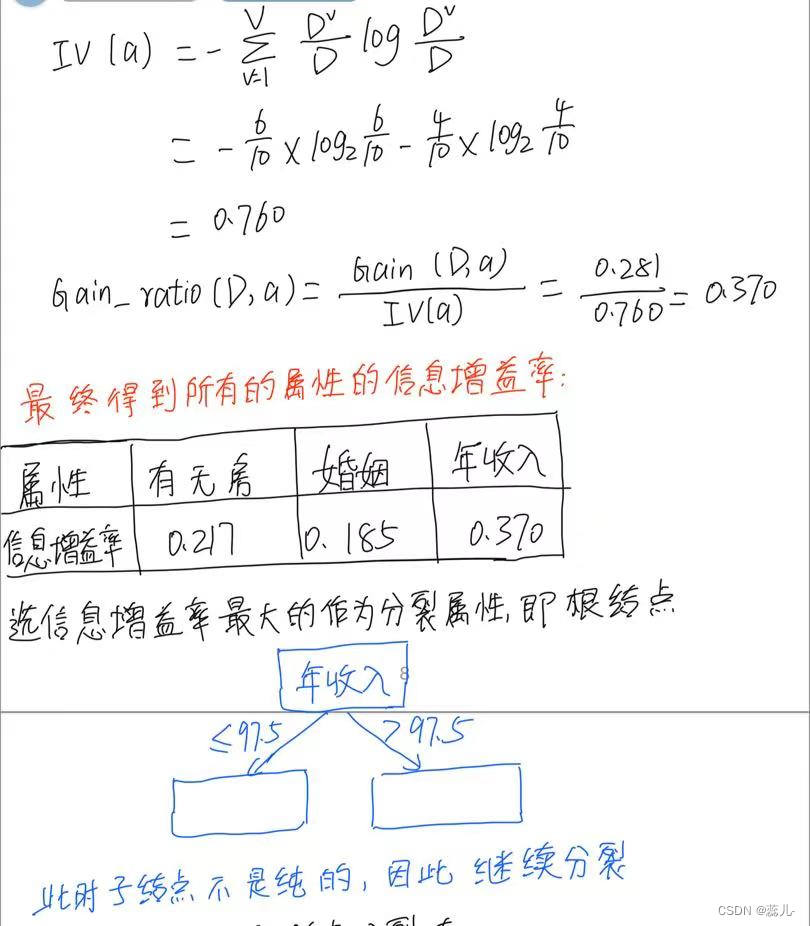
接下来对于年收入<=97.5的样本计算



所以对于<=97.5的结点接下一步以婚姻状况作为叶子结点继续分裂,后面同理直到发现子结点都是纯的
四.python代码
import pandas as pd
import numpy as np
from math import log2
# 读入数据集
data = {'have_house': ['yes', 'no', 'no', 'yes', 'no', 'no', 'yes', 'no', 'no', 'no'],
'marital_status': ['single', 'married', 'single', 'married', 'divorced', 'married', 'divorced', 'single', 'married', 'single'],
'annual_income': [125, 100, 70, 120, 95, 60, 220, 85, 75, 90],
'late_payment': ['no', 'no', 'no', 'no', 'yes', 'no', 'no', 'yes', 'no', 'yes']}
df = pd.DataFrame(data)
# 将文本属性转为数值属性
df['have_house'] = df['have_house'].apply(lambda x: 1 if x == 'yes' else 0) # 如果有房产,转换为1,否则转换为0
df['marital_status'] = df['marital_status'].map({'single': 0, 'married': 1, 'divorced': 2}) # 将婚姻状况转换为0-2的数字,表示单身、已婚和离异
df['late_payment'] = df['late_payment'].apply(lambda x: 1 if x == 'yes' else 0) # 如果拖欠贷款,转换为1,否则转换为0
# 定义C4.5算法所需的函数
def calc_entropy(data):
"""计算信息熵"""
counts = data.value_counts() # 统计各类别样本的数量
probs = counts / len(data) # 计算各类别样本的概率
entropy = -sum(probs * np.log2(probs)) # 根据公式计算信息熵
return entropy
def calc_conditional_entropy(data, feature, threshold):
"""计算条件熵"""
low_subset = data[data[feature] < threshold]['late_payment'] # 获取年收入小于阈值的目标变量列
high_subset = data[data[feature] >= threshold]['late_payment'] # 获取年收入大于等于阈值的目标变量列
prob_low = len(low_subset) / len(data) # 计算前一部分的出现概率
prob_high = len(high_subset) / len(data) # 计算后一部分的出现概率
entropy = prob_low * calc_entropy(low_subset) + prob_high * calc_entropy(high_subset) # 计算条件熵
return entropy
def calc_information_gain(data, feature):
"""计算信息增益"""
base_entropy = calc_entropy(data['late_payment']) # 计算全局信息熵
sorted_values = sorted(data[feature].unique()) # 对连续属性的取值进行排序
thresholds = [(sorted_values[i] + sorted_values[i+1]) / 2 for i in range(len(sorted_values)-1)] # 计算各个分割点的阈值
info_gains = []
for threshold in thresholds:
cond_entropy = calc_conditional_entropy(data, feature, threshold)
info_gain = base_entropy - cond_entropy
info_gains.append(info_gain)
best_threshold_index = np.argmax(info_gains) # 找到信息增益最大的分割点
best_threshold = thresholds[best_threshold_index] # 找到对应的阈值
return info_gains[best_threshold_index], best_threshold
def select_best_feature(data, features):
"""选择最佳特征"""
info_gains = [calc_information_gain(data, feature) for feature in features] # 计算每个特征的信息增益和最佳分割点
best_feature_index = np.argmax([gain for gain, threshold in info_gains]) # 找到信息增益最大的特征
best_feature = features[best_feature_index] # 找到对应的属性名
best_threshold = info_gains[best_feature_index][1] # 找到对应的最佳分割点
return best_feature, best_threshold
def create_tree(data, features):
"""创建决策树"""
target = data['late_payment']
# 如果所有样本都属于同一类别,则停止划分,返回该类别
if len(target.unique()) == 1:
return target.iloc[0]
# 如果没有属性可用于划分,则停止划分,返回样本数最多的类别
if len(features) == 0:
return target.value_counts().idxmax()
# 选择最佳特征进行划分
best_feature, best_threshold = select_best_feature(data, features)
tree = {best_feature: {}}
low_subset = data[data[best_feature] < best_threshold].drop(columns=best_feature)
high_subset = data[data[best_feature] >= best_threshold].drop(columns=best_feature)
sub_features = [f for f in features if f != best_feature]
if len(low_subset) > 0:
low_subtree = create_tree(low_subset, sub_features)
tree[best_feature]['<{}'.format(best_threshold)] = low_subtree
if len(high_subset) > 0:
high_subtree = create_tree(high_subset, sub_features)
tree[best_feature]['>={}'.format(best_threshold)] = high_subtree
return tree
# 构建决策树模型
features = ['have_house', 'marital_status', 'annual_income'] # 特征集合
tree = create_tree(df, features)
print(tree)
输出结果为:
{'annual_income': {'<97.5': {'marital_status': {0: 1, 1: {'have_house': {0: 0, 1: 1}}, 2: 1}}, '>=97.5': {'have_house': {0: 1, 1: 0}}}}
{'annual_income': {'<97.5': {'marital_status': {0: 1, 1: {'have_house': {0: 0, 1: 1}}, 2: 1}}, '>=97.5': {'have_house': {0: 1, 1: 0}}}}
五.优点与改进
C4.5算法是用于生成决策树的一种经典算法,是ID3算法的一种延伸和优化。C4.5算法对ID3算法主要做了一下几点改进:
(1)通过信息增益率选择分裂属性,克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足;
(2)能够处理离散型和连续型的属性类型,即将连续型的属性进行离散化处理;
(3)构造决策树之后进行剪枝操作;
(4)能够处理具有缺失属性值的训练数据。 C4.5算法训练的结果是一个分类模型,这个分类模型可以理解为一个决策树,分裂属性就是一个树节点,分类结果是树的结点。每个节点都有左子树和右子树,结点无左右子树。
(5)C4.5采用二分法处理连续特征,将连续特征进行排列,将连续两个值的中间值作为分裂节点,将小于该值和大于该值的样本分为两个类别,找到信息增益最大的分裂点,本质上还是用的离散特征。需注意的是,与离散属性不同,若当前节点划分属性为连续属性,该属性还可作为其后代节点的划分属性。
(6)在属性值缺失的情况下划分属性,将数据集分成两部分:没有缺失值的部分、有缺失值的部分。对每个样本设置一个权重,将没有缺失值的部分按照占据总样本的比例计算信息增益率,并乘上所占比例。
(7)给定划分属性,若样本在该属性上缺失时,若样本x在划分属性a上的取值未知,则将x同时划入所有子节点,且样本权值按所占比例和样本权值进行调整。直观地看,这就是让同一个样本以不同的概率划入到不同的子节点中。
缺点
信息增益率采用熵的计算,里面有大量耗时的对数计算。
多叉树的计算效率不如二叉树高。
决策树模型容易过拟合,所以应该引入剪枝策略进行处理。
六参考文献:
[1] Quinlan, J.R. (1993). C4.5: Programs for Machine Learning. Morgan Kaufmann Publishers. ISBN 1-55860-238-0.
[2] 周志华. 机器学习. 北京:清华大学出版社,2016.
版权归原作者 蕊儿- 所有, 如有侵权,请联系我们删除。