你是否一直在使用你的损失函数来评估你的机器学习系统的性能?我相信有很多人也是这样做的,这是一个普遍存在的误解,因为人工智能中的程序默认设置、课程中介绍都是这样说的。
在本文中,我将解释为什么需要两个独立的模型评分函数来进行评估和优化……甚至还可能需要第三个模型评分函数来进行统计测试。
在整个数据科学项目,会看到评分指标函数(例如MSE)用于三个主要目的:
- 表现评估:模型表现如何?通过评估指标能快速了解我们在做什么
- 模型优化:模型是否适合,是否可以改进?哪种模型最接近我们的数据点?
- 统计决策:模型是否足以让我们使用?这个模型通过我们严格的假设检验标准了吗?
这三个函数彼此之间有微妙的但很重要的“不同”,所以让我们更深入地看看是什么让一个函数对每个目的都“好”。
表现评估(度量)
性能指标告诉我们模型的表现如何。评估的目的是让任何人看到分数后就能够立刻了解模型的内容。
指标应旨在使人有意义并有效地传达信息。
例如尽管MSE是模型优化的非常流行的指标,但它涉及将我们关心的数字平方,它对指标进行了错误的缩放。所以他对于我们的评估来说并不是一个最佳的指标,因为指标应旨在使人有意义并有效地传达信息。
所以人们更喜欢RMSE,因为RMSE将MSE的数量级缩小到更加可读的范围
所以如何评估一个度量是“好”的?
当性能评估指标被设计用来捕捉人们关心的事情,并有效地将这些信息传递到你的大脑中时,它就是好的。MSE是一个还算不错的指标,但还不是最好的。
模型优化(损失函数)
模型评估函数的第二次使用是为了优化。这时就要用到损失函数了。损失函数是机器学习算法在优化/模型拟合步骤中试图最小化的公式。
当通过数据拟合模型时,我们实际上是在微调一些参数,模型通过这些函数来使其结果尽可能接近数据。通过损失函数的得分来进行优化,它实质上是一种自动方法来确定哪种参数更适合我们的数据。损失函数的结果越大,说明在模型与数据的差异就越多。
对于机器学习来说,能够实现才是最终的目的,所以选择一个易于计算的函数是非常现实的问题,这就是为什么MSE如此受欢迎原因。在微积分X²的一阶导数是非常容易计算的(MSE中的S代表“平方”),因此在优化中 最小化的问题就变得非常的简单。
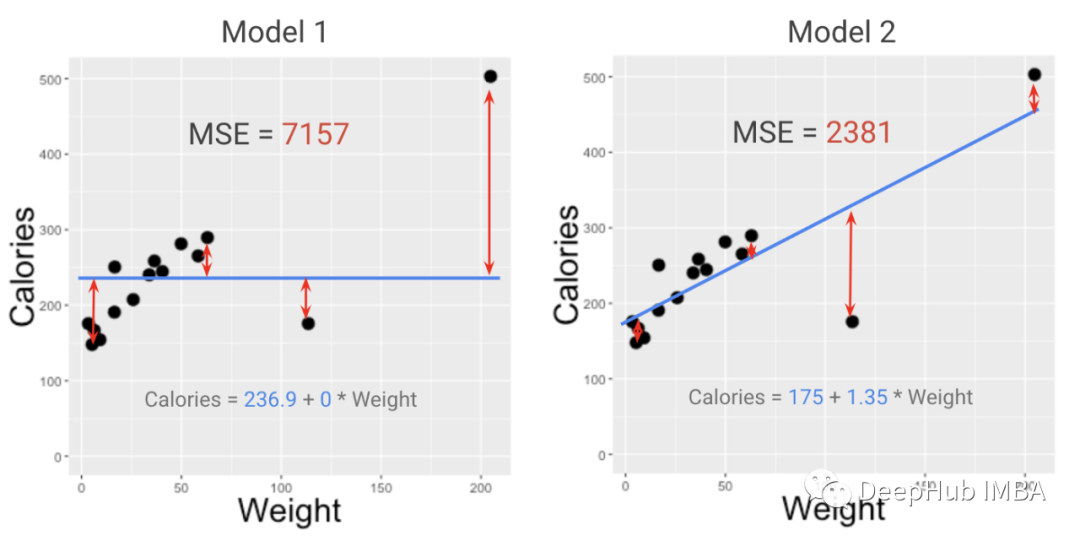
在上面图中,我们从模型1开始,然后用优化算法(也可以叫微积分)得到模型2。我们找到了截距和斜率的值,从而得到了这些数据的最小MSE。模型2是一条根据MSE的最小化计算出的尽可能接近点的直线。
但当涉及到在机器学习算法的框架下优化哪个损失函数时,我们根本无法真正的选择,因为除非你重新发明轮子,从头开始构建优化代码。
在很多情况下我们选择损失函数的决策过程并不是业务和现实世界的解释问题,而是便利性问题
在实际使用时我们使用其他人的成熟算法,因此必须与已经实现的任何损失函数一起使用。他们选择的是最容易优化的产品,但是有时候可能对我们的使用场景并不是最优的。
这就是为什么最终依赖的损失函数是一个便利性问题,而不是适合业务问题或现实世界的解释。
为什么评估函数“有利于”优化?
当损失函数在机器学习算法中被设计为有效工作时,它必须易于机器进行优化(而且它还应该与所关心的任何现实世界的指标保持一致,否则优化它将使模型变得更糟,而不是更好)是非常好的。例如在一般情况下MSE是用于建模连续数据的最佳损失函数……但它也有一些问题——如果你有大量的异常值,可能就要找到其他损失函数了。
统计决策(检验统计)
最后来说一下统计检验,这是描述的模型是否可行的分值(例如系统是否上线)。
为测试选择一个评分函数的想法与性能评估指标类似,但有一个小的不同就是不再强调对于“人”的可读性,而是将重点转移到它作为决策边界的能力和它对假设检验的便利。
与性能评估指标相同的是用于统计测试的指标也必须捕获系统性能中对需要句解决的现实问题最重要和最有意义的信息。所以他与性能评估指标是密切相关的,如果它们不相同,则一般情况下是因为评估指标涉及到统计测试指标的可读性的转换(如改变尺度或取根等,例如MSE和RMSE)。
为什么“得分”函数有利于统计决策测试?
如果一个假设检验统计数据能够准确地反映了两种状态之间的边界,那么它就是好的:因为我们要通过这个分数来判断一个是还是否的问题。所以统计学家会尽可能会把这个统计量转化成便于假设检验并且不会改变边界本身的指标。如果你不是一个统计学家,也不需要担心,因为你很可能永远不会看到它。你只需要知道,这个指标分数是一个正确的决定标准,可以明确的区分是或者不是。
总结
综上所述,我们还是按照提出的三点进行总结:
- 只有新手会使用损失函数进行表现评估;而专家通常使用两个或两个以上的指标。
- 指标是对人“友好的",而损失函数是对机器(程序计算)"友好的"。
- 在应用的ML/AI中,损失函数用于优化,而不是用于统计检验。统计测试应该解决的问题是:“模型的表现是否足以构建/发布?而这里的是否问题应该由业务问题定义。我们不应该改变业务问题陈述来适应损失函数的凸优化目标。
作者:Cassie Kozyrkov