时间序列是由按时间排序的观察单位组成的数据。可能是天气数据、股市数据。,也就是说它是由按时间排序的观察值组成的数据。

在本文中将介绍和解释时间序列的平滑方法,时间序列统计方法在另一篇文章中进行了解释。本文将解释以下 4 个结构概念:
1、稳态(Stationary)
稳态是指系统的状态不再随时间发生改变的一种状态。换句话说,如果一个时间序列的均值、方差和协方差随时间保持不变,则该序列被称为平稳的。
为什么稳态很重要呢?:理论上有一种解释,即时间序列的结构在一定的平稳性下,即在一定的模式下,更容易预测。也就是说,如果是平稳的,则运动下一步也是可以预测的。因此通常会有一个期望:时间序列是平稳的吗?如果它是平稳的,我们可以更容易地做出预测。为了捕捉这一点,可以通过查看时间序列图像而不是统计测试来了解这一点。
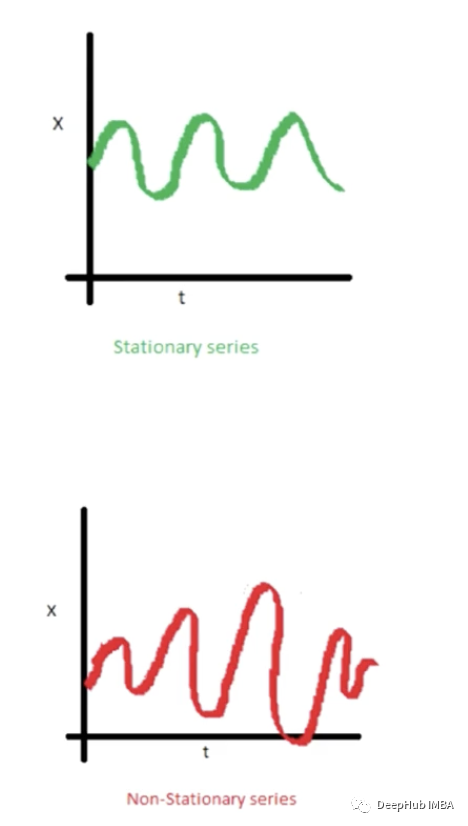
2、趋势(Trend)
它是一个时间序列的长期增减结构。如果存在趋势,则序列不太可能是平稳的,因为周期的统计数据(平均值、标准偏差等)将以增加或减少的趋势变化。
3、季节性(Seasonality)
季节性是指一个时间序列以一定的间隔重复某种行为。
4、周期(Cycle)
它包含类似于季节性的重复模式,但是这两个问题可能会相互混淆。季节性可以映射到特定的时间段。它与日、周、年、季等时间段重叠。例如,市场在周末有更多的生意,或者一个产品在冬天更受关注等等。
周期性发生在更长的时间,更不确定的结构,以不与日、周等结构重叠的方式发生。它的发生主要是出于结构性原因,并具有周期性变化。例如,一些促销活动虽然这不是完全季节性的,它是在一定时期内发生的,但具体会在什么时期发生,会根据不同营销策略来决定。
理解时间序列模型的本质:我们已经看到了上面时间序列的基本结构。时间序列的假设是:时间序列在t时间段内的值受前一个时间段(t-1)的值影响最大。例如今天是星期天,它前面的值最能解释星期天时间序列的值。有了这些基础知识,我们可以开始进行平滑方法的介绍
单变量的平滑方法
1、单指数平滑法(Simple Exponential Smoothing - SES)
它只在平稳的时间序列中表现良好,因为它要求序列中不应该有趋势和季节性。它可以对Level(水平)进行建模(Level可以认为是序列的平均值)。过去的影响是在“未来与最近的过去更相关”的假设上进行加权。SES适用于没有趋势和季节性的单变量时间序列,它在平稳序列中是最成功的。
2、双指数平滑法( Double Exponential Smoothing - DES)
它在SES的基础上增加了趋势的判断。所以它适用于具有和不具有季节性的单变量时间序列。
3、三重指数平滑(TES — Holt-Winters):
它是目前最先进的平滑方法。该方法通过动态评估Level(水平)、趋势和季节性的影响来进行预测。它可以用于具有趋势和/或季节性的单变量序列。
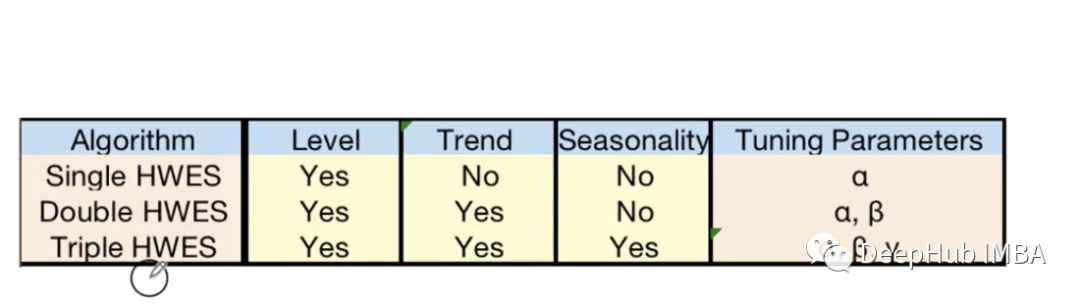
平滑方法使用样例
我们这里将使用来自 sm 模块的数据集。它根据时间显示夏威夷大气中的二氧化碳。记录期间:1958 年 3 月 — 2001 年 12 月
import itertools
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.metrics import mean_absolute_error
from statsmodels.tsa.holtwinters import ExponentialSmoothing
from statsmodels.tsa.holtwinters import SimpleExpSmoothing
from statsmodels.tsa.seasonal import seasonal_decompose
# to split the time series into components
import statsmodels.tsa.api as smt
warnings.filterwarnings('ignore')data = sm.datasets.co2.load_pandas()
# A dataset from the sm module
y = data.data
# target varible
y
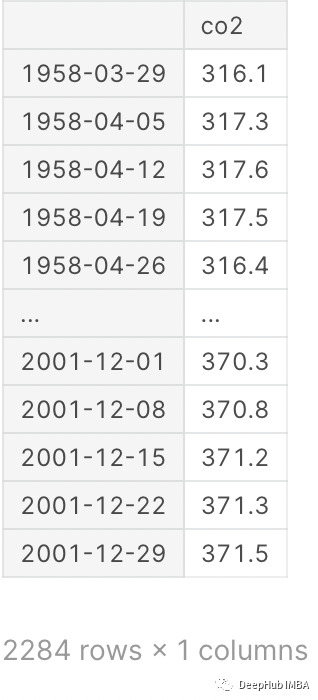
索引为日期, 通过查看日期,可以确定这个数据集是每周一次!如果需要查看每月数据则需要进行转换。
y = y['co2'].resample('MS').mean()
y.isnull().sum()
数据中有缺失值。但是时间序列中的缺失值无法用平均值,中位数填充。所以我们这里用在它之前或之后的值填充,它也可以通过平均它之前和之后的值来填充。
y = y.fillna(y.bfill())
y.isnull().sum() # output => 0
y.plot(figsize=(10, 7))
plt.show()
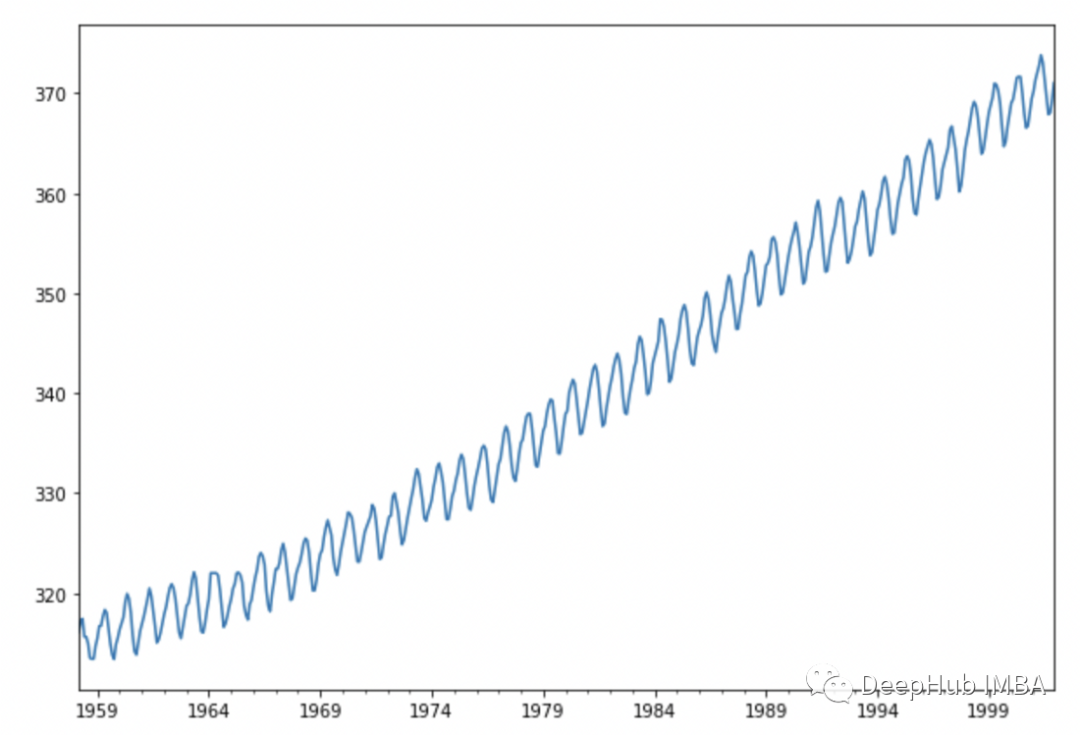
可以看到在这个序列中有一个趋势,也包含了一个很明显的季节性。
我们这里使用 Hold-out 方法是因为模型在训练模型时往往会过度拟合,无论是时间序列还是深度学习方法。因此,我们应该使用一些方法来防止这种情况并更准确地评估错误并验证模型。这就是我们将数据集拆分为训练测试的原因。
train = y[:'1997-12-01']
print("Lenght of train", len(train)) # 478 months
test = y['1998-01-01':]
print("Lenght of test", len(test)) # 48 months
1、SES
SES = Level (Unsuccessful if Trend and Seasonality).
这里有一个“smoothing_level”参数。如果没有输入smoothing_level,方法也不会报错出错。这是因为后面还会有更多的参数,所以这里先暂时设定一个值
ses_model = SimpleExpSmoothing(train).fit(smoothing_level=0.5)
y_pred = ses_model.forecast(48)
可视化函数
def plot_co2(train, test, y_pred, title):
mae = mean_absolute_error(test, y_pred)
train["1985":].plot(legend=True, label="TRAIN", title=f"{title}, MAE: {round(mae,2)}")
test.plot(legend=True, label="TEST", figsize=(6, 4))
y_pred.plot(legend=True, label="PREDICTION")
plt.show()
plot_co2(train, test, y_pred, "Single Exponential Smoothing")
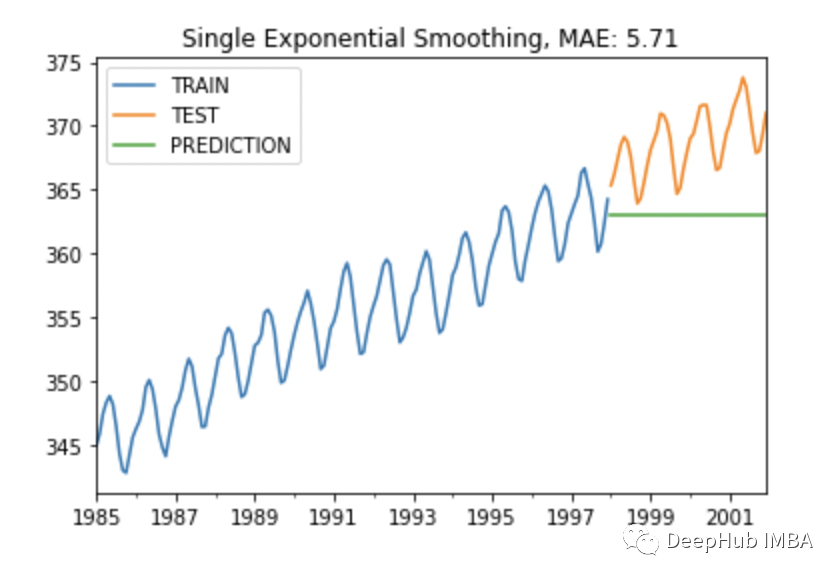
可以看到SES预测的并不好,这是因为我们的序列中包含了季节性相关的信息,我们再做一个微调
def ses_optimizer(train, alphas, step=48): # step for length of test set
best_alpha, best_mae = None, float("inf")
for alpha in alphas:
ses_model = SimpleExpSmoothing(train).fit(smoothing_level=alpha)
y_pred = ses_model.forecast(step)
mae = mean_absolute_error(test, y_pred)
if mae < best_mae:
best_alpha, best_mae = alpha, mae
print("alpha:", round(alpha, 2), "mae:", round(mae, 4))
print("best_alpha:", round(best_alpha, 2), "best_mae:", round(best_mae, 4))
return best_alpha, best_mae
alphas = np.arange(0.8, 1, 0.01)
从0.8到1的0.01步生成alpha。如果愿意,可以以0.1为增量从0.1写到1,但SES已经是一个弱模型,接近历史真实值将产生更好的结果,所以我们从0.8开始。
best_alpha, best_mae = ses_optimizer(train, alphas)
# best_alpha: 0.99 best_mae: 4.5451
最后的模型参数是这样的:
ses_model = SimpleExpSmoothing(train).fit(smoothing_level=best_alpha)
y_pred = ses_model.forecast(48)
plot_co2(train, test, y_pred, "Single Exponential Smoothing")
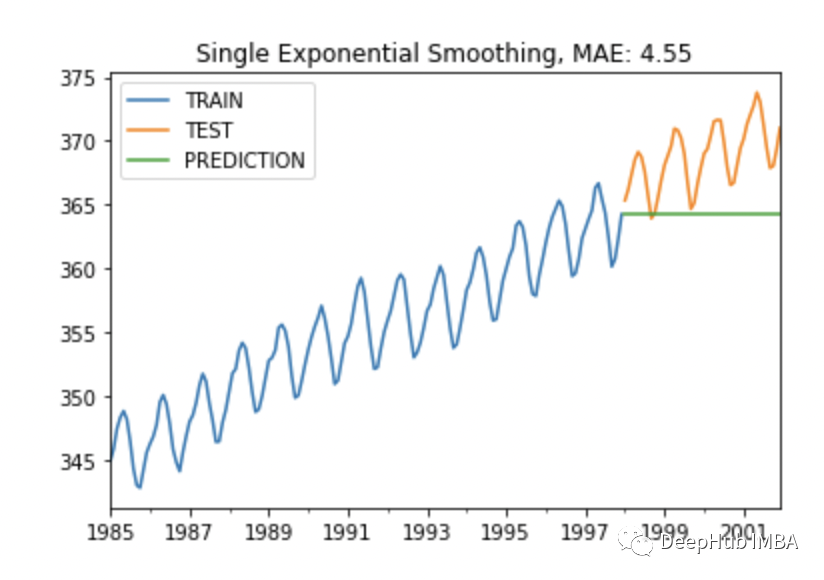
MAE有所降低但是其实还是不怎么样,对吧.
2、DES
DES: Level (SES) + Trend
这些级数可以是乘法也可以是加法,例如
- y(t) = Level + Trend + Seasonality + Noise => 加
- y(t) = Level *Trend * Seasonality * Noise => 乘
在乘法运算中,结构的变化更具依赖性。如果季节性和残差与趋势无关,则该级数是可加的。如果季节性和残差根据趋势形成,则是相乘的。
季节性和残差随机分布在0附近。所以可以确定趋势并没有影响残差,所以这个我们确定这个级数是加性的。
通常我们应该建立两个模型,并决定使用有较低的误差的模型。但是在这里确认残差和季节性与趋势无关。所以直接使用“add”参数。
des_model = ExponentialSmoothing(train, trend="add").fit(smoothing_level=0.5, smoothing_trend=0.5)
y_pred = des_model.forecast(48)
plot_co2(train, test, y_pred, "Double Exponential Smoothing")
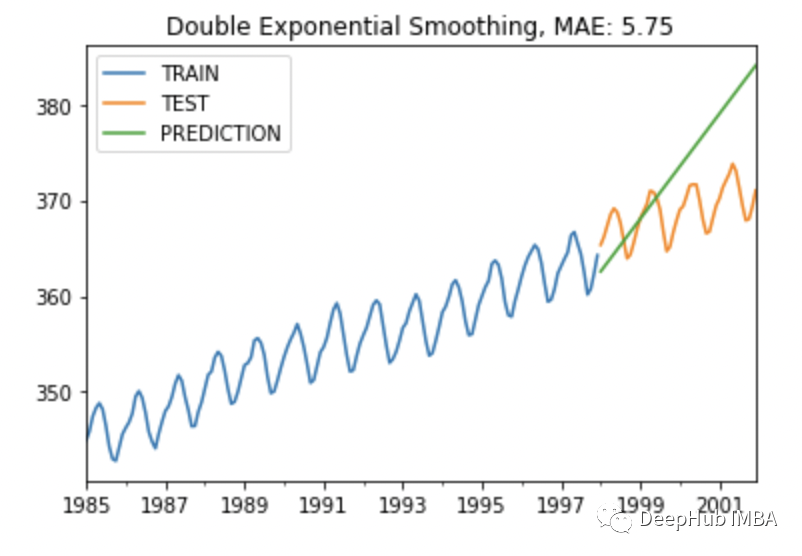
虽然结果看起来不错,已经捕捉到了趋势,但由于缺乏季节性,这个估计也不太好,我们继续优化
def des_optimizer(train, alphas, betas, step=48):
best_alpha, best_beta, best_mae = None, None, float("inf")
for alpha in alphas:
for beta in betas:
des_model = ExponentialSmoothing(train, trend="add").fit(smoothing_level=alpha, smoothing_slope=beta)
y_pred = des_model.forecast(step)
mae = mean_absolute_error(test, y_pred)
if mae < best_mae:
best_alpha, best_beta, best_mae = alpha, beta, mae
print("alpha:", round(alpha, 2), "beta:", round(beta, 2), "mae:", round(mae, 4))
print("best_alpha:", round(best_alpha, 2), "best_beta:", round(best_beta, 2), "best_mae:", round(best_mae, 4))
return best_alpha, best_beta, best_maealphas = np.arange(0.01, 1, 0.10)
betas = np.arange(0.01, 1, 0.10)
best_alpha, best_beta, best_mae = des_optimizer(train, alphas, betas)
最终的模型参数:
final_des_model = ExponentialSmoothing(train, trend="add").fit(smoothing_level=best_alpha, smoothing_slope=best_beta)
y_pred = final_des_model.forecast(48)
plot_co2(train, test, y_pred, "Double Exponential Smoothing")
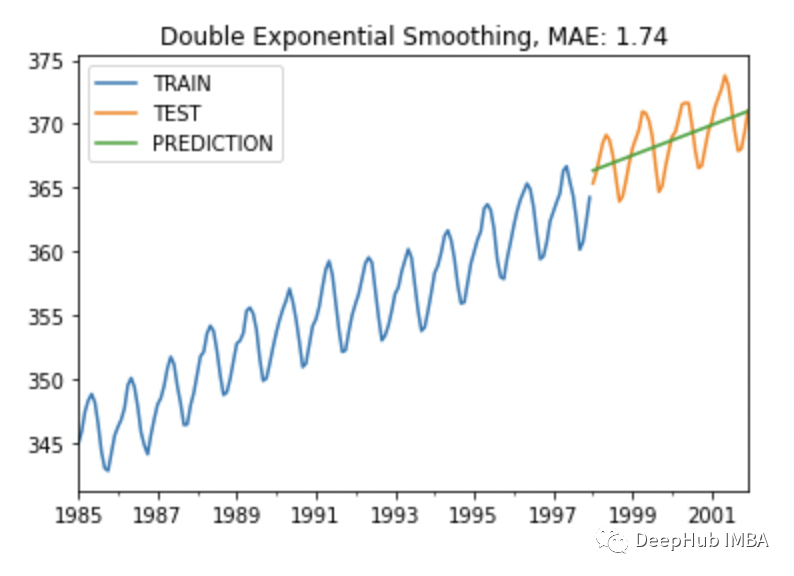
MAE小了很多,趋势也很平稳,但是没有季节性
3、TES
TES = SES + DES + Seasonality
当我们输入趋势和季节性作为参数时,将使用 TES。
tes_model = ExponentialSmoothing(train,
trend="add",
seasonal="add",
seasonal_periods=12)
.fit(smoothing_level=0.5,smoothing_slope=0.5,smoothing_seasonal=0.5)
我们把季节性周期 设为12,因为数据集中的年份是由月份决定的。也就是说我们确定季节性的周期是12个月(1年)
y_pred = tes_model.forecast(48)
plot_co2(train, test, y_pred, "Triple Exponential Smoothing")
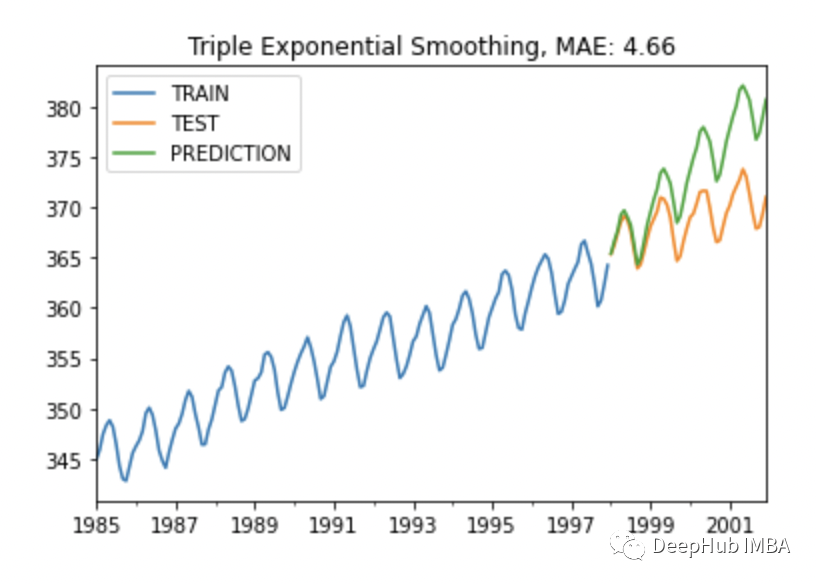
可以看到,趋势和季节性都有了,我们继续优化
alphas = betas = gammas = np.arange(0.20, 1, 0.10)
这里有包含了3个超参数:
abg = list(itertools.product(alphas, betas, gammas))
def tes_optimizer(train, abg, step=48):
best_alpha, best_beta, best_gamma, best_mae = None, None, None, float("inf")
for comb in abg:
tes_model = ExponentialSmoothing(train, trend="add", seasonal="add", seasonal_periods=12).\
fit(smoothing_level=comb[0], smoothing_slope=comb[1], smoothing_seasonal=comb[2])
# her satırın 0., 1., 2. elemanlarını seç ve model kur
y_pred = tes_model.forecast(step)
mae = mean_absolute_error(test, y_pred)
if mae < best_mae:
best_alpha, best_beta, best_gamma, best_mae = comb[0], comb[1], comb[2], mae
# print([round(comb[0], 2), round(comb[1], 2), round(comb[2], 2), round(mae, 2)])
print("best_alpha:", round(best_alpha, 2), "best_beta:", round(best_beta, 2), "best_gamma:", round(best_gamma, 2),
"best_mae:", round(best_mae, 4))
return best_alpha, best_beta, best_gamma, best_mae
best_alpha, best_beta, best_gamma, best_mae = tes_optimizer(train, abg)
# best_alpha: 0.8 best_beta: 0.5 best_gamma: 0.7 best_mae: 0.606
上面给出的参数 smoothing_slope 与 smoothing_trend 相同。此处使用 smoothing_trend 来表明它们是相同的,看看结果:
final_tes_model = ExponentialSmoothing(train, trend="add", seasonal="add", seasonal_periods=12).\
fit(smoothing_level=best_alpha, smoothing_trend=best_beta, smoothing_seasonal=best_gamma)
y_pred = final_tes_model.forecast(48)
plot_co2(train, test, y_pred, "Triple Exponential Smoothing")
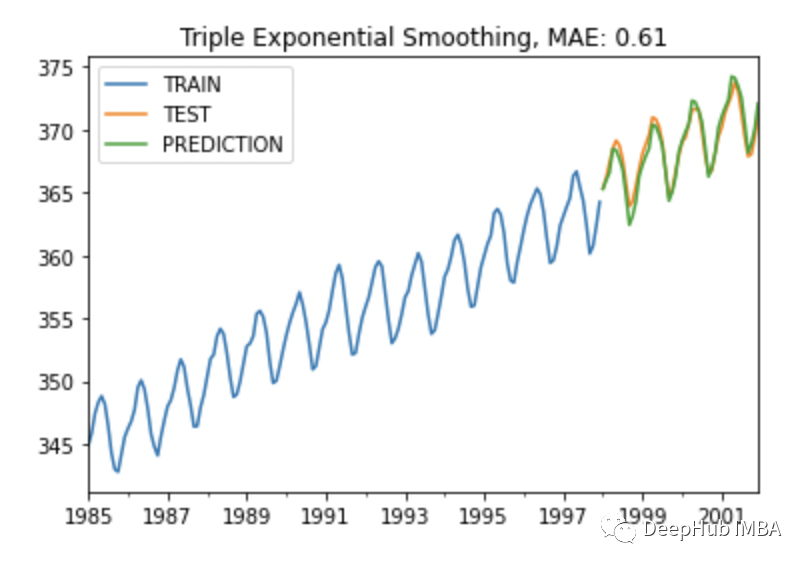
无论从MAE还是可视化的结果看,都很不错,对吧。
总结
以上就是三个平滑方法的介绍,本文的完整代码:https://github.com/furkannakdagg/time_series_tutorial/blob/main/time-series-smoothing-methods-tutorial.ipynb
作者:Furkan Akdağ