文章目录
1. 摄像头的成像原理
视觉传感器：利用光学元件和成像装置获取外部环境图像信息的仪器。
通常视觉传感器，其主要功能是获取足够的机器视觉系统要处理的最原始图像，类似于人类的眼睛。
1.1 单目视觉传感器的硬件结构
单目视觉的相机模组的组件包括了lens(镜头)、分色滤色片(IR cut)、感光元件等。
分色滤色片：对色光具有吸收、反射和透过作用的染有颜色的透明片。目前分色滤色片有两种分色方法：RGB原色分色法，CMYK补色分色法
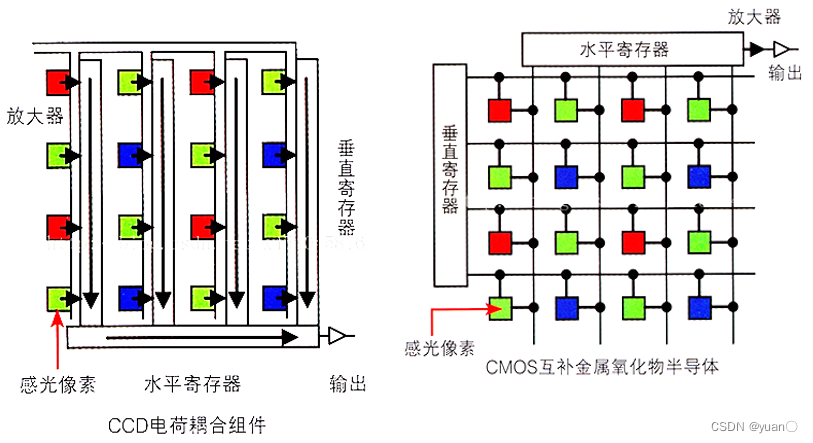感光元件，其表面包含有几十万到几百万的光电二极管。光电二极管受到光照射时，就会产生电荷。感光元件一般包括CCD和CMOS两种。像素值一般为（0-255），电路噪声导致像素值失真.
1.2 单目视觉的成像原理 –小孔成像模型
成像模型：相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素）的过程。
相机坐标系：
O
−
x
−
y
−
z
O−x−y−z
O−x−y−z 为相机坐标系，在轴指向相机前方，
x
x
x轴向右，
y
y
y轴向下。
O
O
O为摄像机的光心（或摄像头中心）。
物理成像平面：
O
’
−
x
’
−
y
’
−
z
’
O’−x’−y’−z’
O’−x’−y’−z’为物理成像平面。物理成像平面到小孔的距离为
f
f
f，称之为焦距。
成像原理：空间点
P
P
P的光束被映射到图像平面，图像平面感光之后形成像素
P
′
P'
P′。
接下来看看具体的原理推导：
首先，已知三维世界中的坐标点
P
=
（
X
,
Y
,
Z
）
P=（X,Y,Z）
P=（X,Y,Z）,成像平面中的
P
′
=
(
X
′
,
Y
′
)
P'=(X',Y')
P′=(X′,Y′)，焦距为
f
f
f.由相似三角形原理可得，
X
′
=
−
f
⋅
X
Z
Y
′
=
−
f
⋅
Y
Z
\begin{array}{c}X' = - \frac{{f \cdot X}}{Z}\\\\Y' = - \frac{{f \cdot Y}}{Z}\end{array}
X′=−Zf⋅XY′=−Zf⋅Y 在视觉感知中，常使用等效表达的方式来体现真实图像的输出过程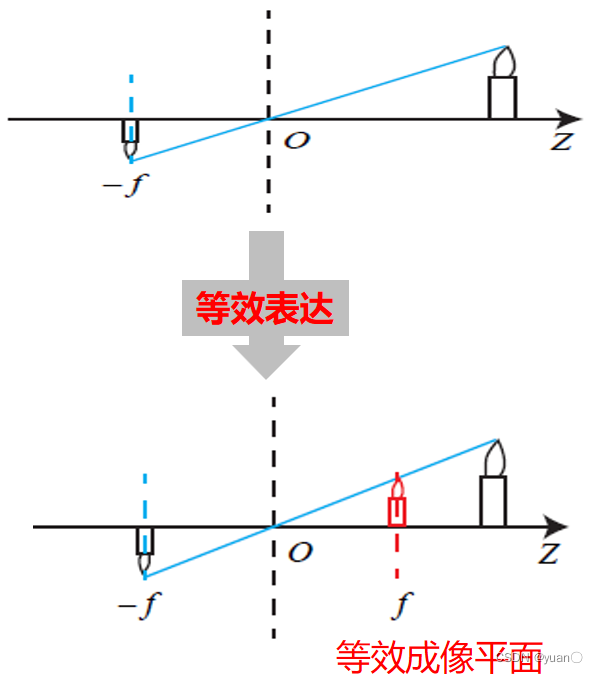 因此，我们可以将式子改为
X
′
=
f
⋅
X
Z
Y
′
=
f
⋅
Y
Z
\begin{array}{c}X' = \frac{{f \cdot X}}{Z}\\\\Y' = \frac{{f \cdot Y}}{Z}\end{array}
X′=Zf⋅XY′=Zf⋅Y
1.3 单目视觉的成像原理 – 像素坐标系
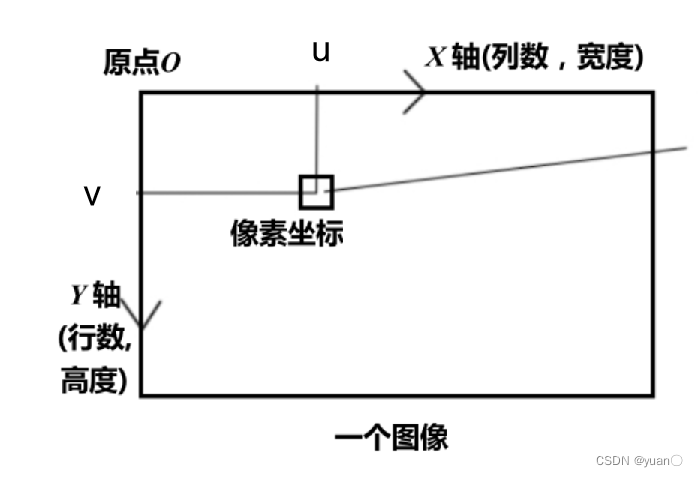
从成像平面坐标到像素坐标：图像是基于像素来表达。像素坐标和成像平面坐标之间，相差了一个缩放和原点的平移。
假设正向成像平面中
P
’
=
(
X
’
,
Y
’
)
P’=(X’, Y’)
P’=(X’,Y’), 其像素坐标为
(
u
,
v
)
(u, v)
(u,v).
缩放及平移的过程可以由下式来表达：
{
u
=
α
X
′
+
c
x
v
=
β
Y
′
+
c
y
\left\{ {\begin{array}{ccccccccccccccc}{u = \alpha X' + {c_x}}\\{v = \beta Y' + {c_y}}\end{array}} \right.
{u=αX′+cxv=βY′+cy 将
P
′
P'
P′的坐标代入，
X
′
=
f
⋅
X
Z
，
Y
′
=
f
⋅
Y
Z
\begin{array}{c}X' = \frac{{f \cdot X}}{Z}，Y' = \frac{{f \cdot Y}}{Z}\end{array}
X′=Zf⋅X，Y′=Zf⋅Y，可以得到三维坐标与像素坐标的转换关系
{
u
=
f
x
X
Z
+
c
x
v
=
f
y
Y
Z
+
c
y
f
x
=
α
f
,
f
y
=
β
f
\begin{array}{l}\left\{ {\begin{array}{ccccccccccccccc}{u = {f_x}\frac{X}{Z} + {c_x}}\\{v = {f_y}\frac{Y}{Z} + {c_y}}\end{array}} \right.\\{f_x} = \alpha f,{f_y} = \beta f\end{array}
{u=fxZX+cxv=fyZY+cyfx=αf,fy=βf 用矩阵的形式表达：
[
μ
ν
1
]
=
1
Z
[
f
x
0
c
x
0
f
y
c
y
0
0
1
]
[
X
Y
Z
]
\left[ {\begin{array}{ccccccccccccccc}\mu \\\nu \\1\end{array}} \right] = \frac{1}{Z}\left[ {\begin{array}{ccccccccccccccc}{{f_x}}&0&{{c_x}}\\0&{{f_y}}&{{c_y}}\\0&0&1\end{array}} \right]\left[ {\begin{array}{ccccccccccccccc}X\\Y\\Z\end{array}} \right]
μν1=Z1fx000fy0cxcy1XYZ 其中，
[
μ
ν
1
]
\left[ {\begin{array}{ccccccccccccccc}\mu \\\nu \\1\end{array}} \right]
μν1为像素坐标，
[
X
Y
Z
]
\left[ {\begin{array}{ccccccccccccccc}X\\Y\\Z\end{array}} \right]
XYZ为相机坐标系中的三维坐标点，
[
f
x
0
c
x
0
f
y
c
y
0
0
1
]
\left[ {\begin{array}{ccccccccccccccc}{{f_x}}&0&{{c_x}}\\0&{{f_y}}&{{c_y}}\\0&0&1\end{array}} \right]
fx000fy0cxcy1为内参矩阵。
1.4 单目视觉三维坐标系转换 – 外参
相机的三维坐标系(
O
C
O_C
OC) 并不是一个“稳定”的坐标系，会随着相机的移动而改变坐标的原点和各个坐标轴的方向。在应用中，相机安装在自动驾驶车辆上，随车辆运动相机坐标系实时变化。对一些需要固定特征坐标的应用，比如地图，因此需要引进一个稳定不变的坐标系：世界坐标系（
O
W
O_W
OW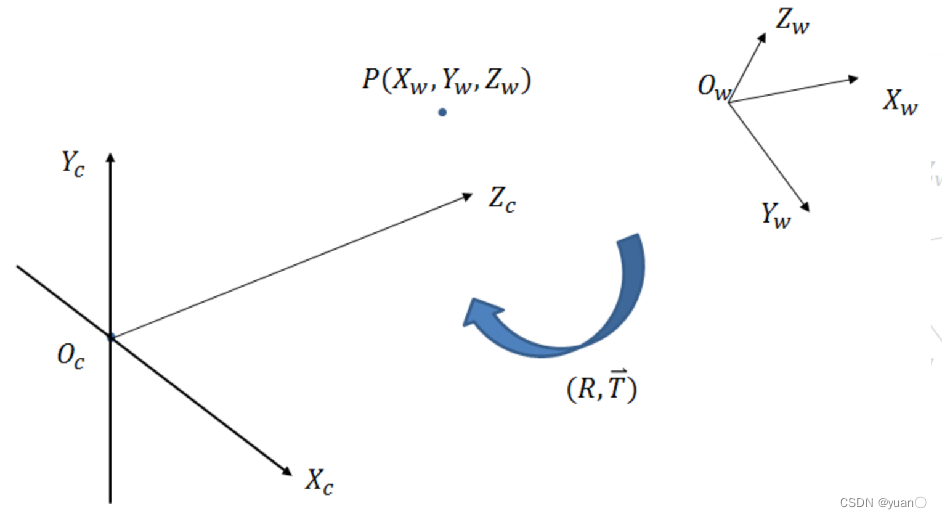） 从某三维世界坐标系（
O
W
O_W
OW）到相机的三维坐标系(
O
C
O_C
OC)的变换，称为**相机的外参**，本质是将世界坐标系中的特征点，转换到相机坐标系。
三维坐标系的变换是一个刚性平移加旋转的过程，变换包括平移向量（
t
t
t：3x1）以及旋转矩阵(
R
R
R：3x3)。
三维坐标变换表达：已知某世界坐标系(
O
W
O_W
OW)中空间点
P
W
=
(
X
W
,
Y
W
,
Z
W
)
P_W =(X_W, Y_W, Z_W)
PW=(XW,YW,ZW)以及
O
W
O_W
OW与相机坐标系(
O
C
O_C
OC)的变换
R
,
t
R,t
R,t. 求解此空间点在OC坐标系的坐标
P
C
=
(
X
C
,
Y
C
,
Z
C
)
P_C =(X_C, Y_C, Z_C)
PC=(XC,YC,ZC) 。
下式即为三维坐标变换：
[
X
c
Y
c
Z
c
]
=
[
R
11
R
12
R
13
R
21
R
22
R
23
R
31
R
32
R
33
]
[
X
w
Y
w
Z
w
]
+
[
t
1
t
2
t
3
]
\left[ {\begin{array}{ccccccccccccccc}{{X_c}}\\{{Y_c}}\\{{Z_c}}\end{array}} \right] = \left[ {\begin{array}{ccccccccccccccc}{{R_{11}}}&{{R_{12}}}&{{R_{13}}}\\{{R_{21}}}&{{R_{22}}}&{{R_{23}}}\\{{R_{31}}}&{{R_{32}}}&{{R_{33}}}\end{array}} \right]\left[ {\begin{array}{ccccccccccccccc}{{X_w}}\\{{Y_w}}\\{{Z_w}}\end{array}} \right] + \left[ {\begin{array}{ccccccccccccccc}{{t_1}}\\{{t_2}}\\{{t_3}}\end{array}} \right]
XcYcZc=R11R21R31R12R22R32R13R23R33XwYwZw+t1t2t3
1.5 单目视觉的坐标系转换 – 从世界坐标点到像素坐标
最后对整个过程进行总结：
世界坐标系(
O
W
O_W
OW)中空间点
P
W
=
(
X
W
,
Y
W
,
Z
W
)
P_W =(X_W, Y_W, Z_W)
PW=(XW,YW,ZW)，成像到相机中得出其像点
p
=
(
u
,
v
)
p=(u,v)
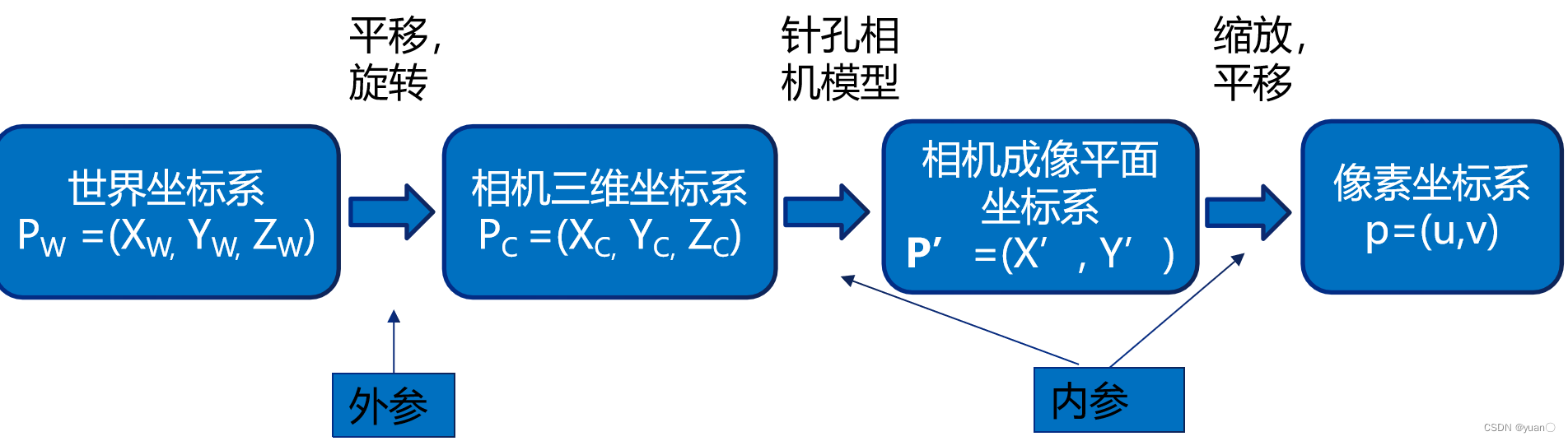
p=(u,v)，需要经过三次变换:
- 世界坐标系转换到相机三维坐标系→ 刚性变化，平移加旋转
- 相机三维坐标系转换到相机成像平面坐标系 → 小孔成像模型
- 相机成像坐标系转换到像素坐标系 →缩放加平移
1.6 单目视觉的特性
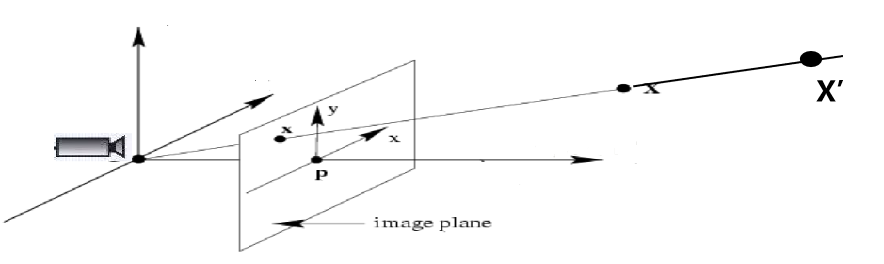
- 深度不确定：图中点X以及点X’的成像点是同一个像素点x。
- 远小近大：高度为X的物体，离相机越远成像点越矮，远处看不见。
- 易受遮挡：X与X’同时存在时，只能看到X，有盲区
- 受光线强度影响：光线过强，都是255，光线过暗，都是0
- 受分辨率影响：像素过低，细节就会丢失
- 受帧率影响：像素过高，传输速率有限，图片帧率偏低
- 受镜头影响：焦距和视角会直接决定看见的距离和角度范围
2. 视觉传感器的标定
首先对成像公式进行整理：
[
μ
ν
1
]
=
1
Z
C
[
f
x
0
c
x
0
f
y
c
y
0
0
1
]
[
X
C
Y
C
Z
C
]
=
1
Z
C
⋅
K
⋅
[
X
C
Y
C
Z
C
]
=
[
μ
ν
1
]
=
1
Z
C
[
f
x
0
c
x
0
f
y
c
y
0
0
1
]
[
X
C
Y
C
Z
C
]
=
1
Z
C
⋅
K
⋅
(
R
⋅
[
X
W
Y
W
Z
W
]
+
t
)
=
1
Z
C
⋅
K
⋅
(
[
R
t
0
1
]
[
X
W
Y
W
Z
W
1
]
)
=
M
⋅
[
X
W
Y
W
Z
W
1
]
=
[
M
1
M
2
M
3
M
4
M
5
M
6
M
7
M
8
M
9
M
10
M
11
M
12
]
⋅
[
X
W
Y
W
Z
W
1
]
\begin{array}{c}\left[ {\begin{array}{ccccccccccccccc}\mu \\\nu \\1\end{array}} \right] = \frac{1}{{{Z_C}}}\left[ {\begin{array}{ccccccccccccccc}{{f_x}}&0&{{c_x}}\\0&{{f_y}}&{{c_y}}\\0&0&1\end{array}} \right]\left[ {\begin{array}{ccccccccccccccc}{{X_C}}\\{{Y_C}}\\{{Z_C}}\end{array}} \right]\\ = \frac{1}{{{Z_C}}} \cdot K \cdot \left[ {\begin{array}{ccccccccccccccc}{{X_C}}\\{{Y_C}}\\{{Z_C}}\end{array}} \right]\\ = \left[ {\begin{array}{ccccccccccccccc}\mu \\\nu \\1\end{array}} \right] = \frac{1}{{{Z_C}}}\left[ {\begin{array}{ccccccccccccccc}{{f_x}}&0&{{c_x}}\\0&{{f_y}}&{{c_y}}\\0&0&1\end{array}} \right]\left[ {\begin{array}{ccccccccccccccc}{{X_C}}\\{{Y_C}}\\{{Z_C}}\end{array}} \right]\\ = \frac{1}{{{Z_C}}} \cdot K \cdot \left( {R \cdot \left[ {\begin{array}{ccccccccccccccc}{{X_W}}\\{{Y_W}}\\{{Z_W}}\end{array}} \right] + t} \right)\\ = \frac{1}{{{Z_C}}} \cdot K \cdot \left( {\left[ {\begin{array}{ccccccccccccccc}R&t\\0&1\end{array}} \right]\left[ {\begin{array}{ccccccccccccccc}{{X_W}}\\{{Y_W}}\\{{Z_W}}\\1\end{array}} \right]} \right)\\ = M \cdot \left[ {\begin{array}{ccccccccccccccc}{{X_W}}\\{{Y_W}}\\{{Z_W}}\\1\end{array}} \right]\\ = \left[ \begin{array}{l}\begin{array}{ccccccccccccccc}{{M_1}}&{{M_2}}&{{M_3}}&{{M_4}}\end{array}\\\begin{array}{ccccccccccccccc}{{M_5}}&{{M_6}}&{{M_7}}&{{M_8}}\end{array}\\\begin{array}{ccccccccccccccc}{{M_9}}&{{M_{10}}}&{{M_{11}}}&{{M_{12}}}\end{array}\end{array} \right] \cdot \left[ {\begin{array}{ccccccccccccccc}{{X_W}}\\{{Y_W}}\\{{Z_W}}\\1\end{array}} \right]\end{array}
μν1=ZC1fx000fy0cxcy1XCYCZC=ZC1⋅K⋅XCYCZC=μν1=ZC1fx000fy0cxcy1XCYCZC=ZC1⋅K⋅R⋅XWYWZW+t=ZC1⋅K⋅[R0t1]XWYWZW1=M⋅XWYWZW1=M1M2M3M4M5M6M7M8M9M10M11M12⋅XWYWZW1
2.1 视觉传感器标定原理 – 线性标定法
标定的数学表达解释：输入
n
n
n个特征点的世界坐标及像素坐标，输出
M
M
M矩阵
原理：根据一对特征点
P
i
,
p
i
P_i , p_i
Pi,pi ，成像公式可以得到两个线性方程:
[
μ
ν
1
]
=
[
M
1
M
2
M
3
M
4
M
5
M
6
M
7
M
8
M
9
M
10
M
11
M
12
]
⋅
[
X
i
Y
i
Z
i
1
]
{\left[ {\begin{array}{ccccccccccccccc}\mu \\\nu \\1\end{array}} \right] = \left[ {\begin{array}{lllllllllllllll}{\begin{array}{ccccccccccccccc}{{M_1}}&{{M_2}}&{{M_3}}&{{M_4}}\end{array}}\\{\begin{array}{ccccccccccccccc}{{M_5}}&{{M_6}}&{{M_7}}&{{M_8}}\end{array}}\\{\begin{array}{ccccccccccccccc}{{M_9}}&{{M_{10}}}&{{M_{11}}}&{{M_{12}}}\end{array}}\end{array}} \right] \cdot \left[ {\begin{array}{ccccccccccccccc}{{X_i}}\\{{Y_i}}\\{{Z_i}}\\1\end{array}} \right]}
μν1=M1M2M3M4M5M6M7M8M9M10M11M12⋅XiYiZi1
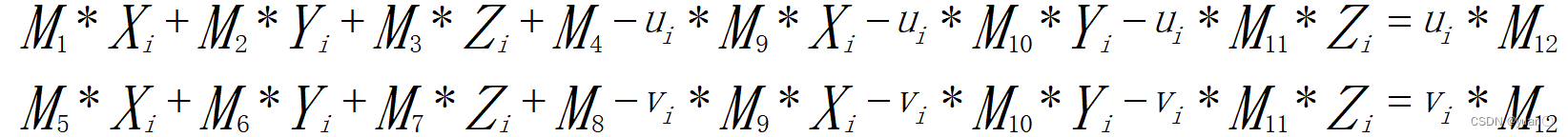
每一对特征点可以转换为两个线性方程，共11个自由度
所以，如果
n
>
=
6
n>=6
n>=6，即可计算得到
M
M
M矩阵
实际应用中，一般会用非常多的特征点，基于最小二乘方法求解
M
M
M矩阵。
如果镜头畸变需要矫正，则需要基于非线性方法，引入非线性畸变模型。一般可以采用非线性优化的方法求解。
2.2 相机畸变模型
2.2.1 径向畸变
由镜头透镜形状引起的畸变称为径向畸变，径向畸变主要分为桶形畸变和枕型畸变。
在针孔相机模型中，一条直线投影到像素平面上还是一条直线。 但在实际中，相机的透镜使得真实环境中的直线在图片中变成了曲线。由于透镜往往是中心对称的，这使得不规则畸变通常径向对称。径向畸变可由三个参数
k
1
,
k
2
,
k
3
k_1,k_2,k_3
k1,k2,k3确定。
x
c
o
r
r
e
c
t
e
d
=
x
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
y
c
o
r
r
e
c
t
e
d
=
y
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
\begin{array}{l}{x_{corrected}} = x(1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6})\\{y_{corrected}} = y(1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6})\end{array}
xcorrected=x(1+k1r2+k2r4+k3r6)ycorrected=y(1+k1r2+k2r4+k3r6)
2.2.2 切向畸变
切向畸变源于透镜不完全平行于图像平面，即感光成像平面装配时与镜头间的角度不准；
产生的影响是图像像素点以畸变中心为中心点，沿着切向产生的位置偏差；
切向畸变由两个参数
p
1
,
p
2
p_1,p_2
p1,p2确定。
x
c
o
r
r
e
c
t
e
d
=
x
+
[
2
p
1
x
y
+
p
2
(
r
2
+
2
x
2
)
]
y
c
o
r
r
e
c
t
e
d
=
y
+
[
p
1
(
r
2
+
2
y
2
)
+
2
p
2
x
y
]
\begin{array}{l}{x_{corrected}} = x + [2{p_1}xy + {p_2}({r^2} + 2{x^2})]\\{y_{corrected}} = y + [{p_1}({r^2} + 2{y^2}) + 2{p_2}xy]\end{array}
xcorrected=x+[2p1xy+p2(r2+2x2)]ycorrected=y+[p1(r2+2y2)+2p2xy]
结合径向畸变的式子，即可得到畸变矫正的公式：
x
c
o
r
r
e
c
t
e
d
=
x
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
+
2
p
1
x
y
+
p
2
(
r
2
+
2
x
2
)
y
c
o
r
r
e
c
t
e
d
=
y
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
+
p
1
(
r
2
+
2
y
2
)
+
2
p
2
x
y
\begin{array}{l}{x_{corrected}} = x(1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}) + 2{p_1}xy + {p_2}({r^2} + 2{x^2})\\{y_{corrected}} = y(1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}) + {p_1}({r^2} + 2{y^2}) + 2{p_2}xy\end{array}
xcorrected=x(1+k1r2+k2r4+k3r6)+2p1xy+p2(r2+2x2)ycorrected=y(1+k1r2+k2r4+k3r6)+p1(r2+2y2)+2p2xy
2.3 单目相机标定方法
对于单目相机的标定，我们主要需要对以下几个量进行标定：
- 内参矩阵 K K K
- 外参 R , t R,t R,t
- 畸变参数 k 1 , k 2 , p 1 , p 2 k_1,k_2,p_1,p_2 k1,k2,p1,p2 有几种常用的方法用于标定：
一步法：
直接使用最优化方法求出相机内外参数
两步法：
- Tsai法（1987年） 假设： u 0 , v 0 u_0,v_0 u0,v0已知，只考虑径向畸变 标定设备：三维标定块
- 张正友法 假设：只考虑径向畸变 标定设备：平面标定板
2.4 双目相机标定
此部分来源于北京理工大学慕课《无人驾驶车辆》
2.4.1 双目相机模型
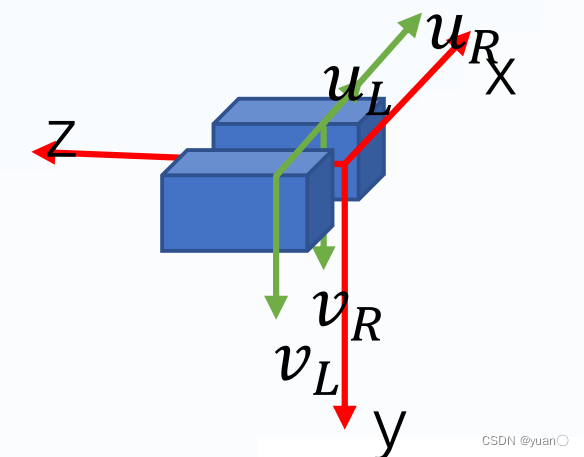
左右双目相机有以下特点：
• 光圈中心都在x轴上
• 光圈中心距离称为“基线
将其转化为俯视图，如下所示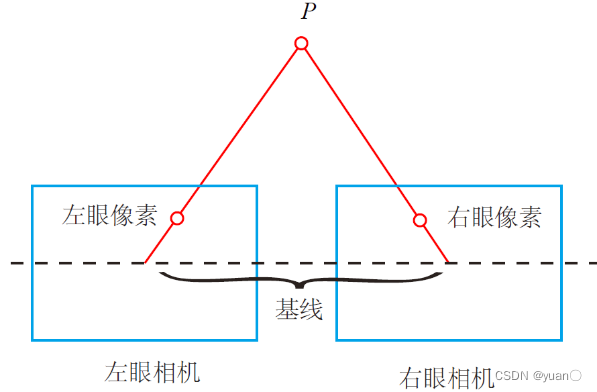
双目相机有以下几何关系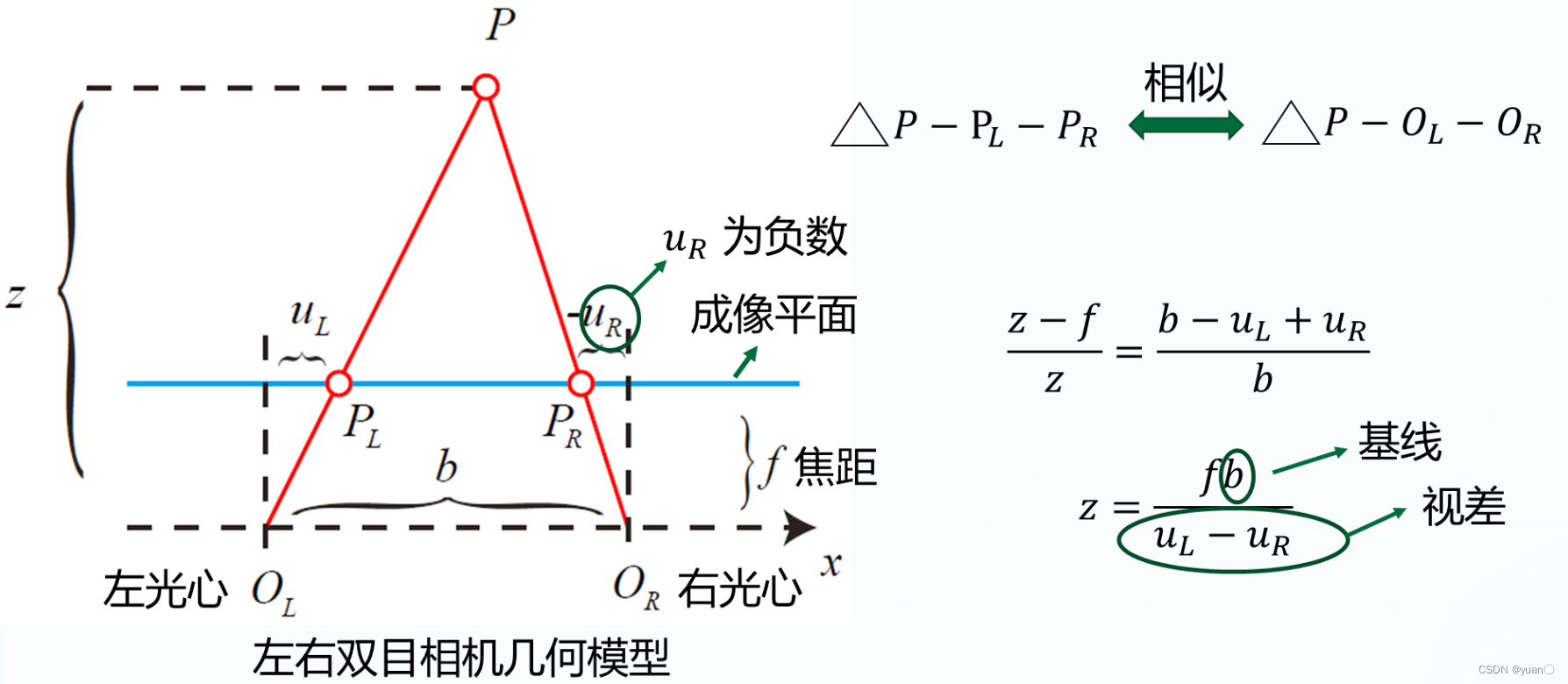
2.4.2 双目相机标定方法
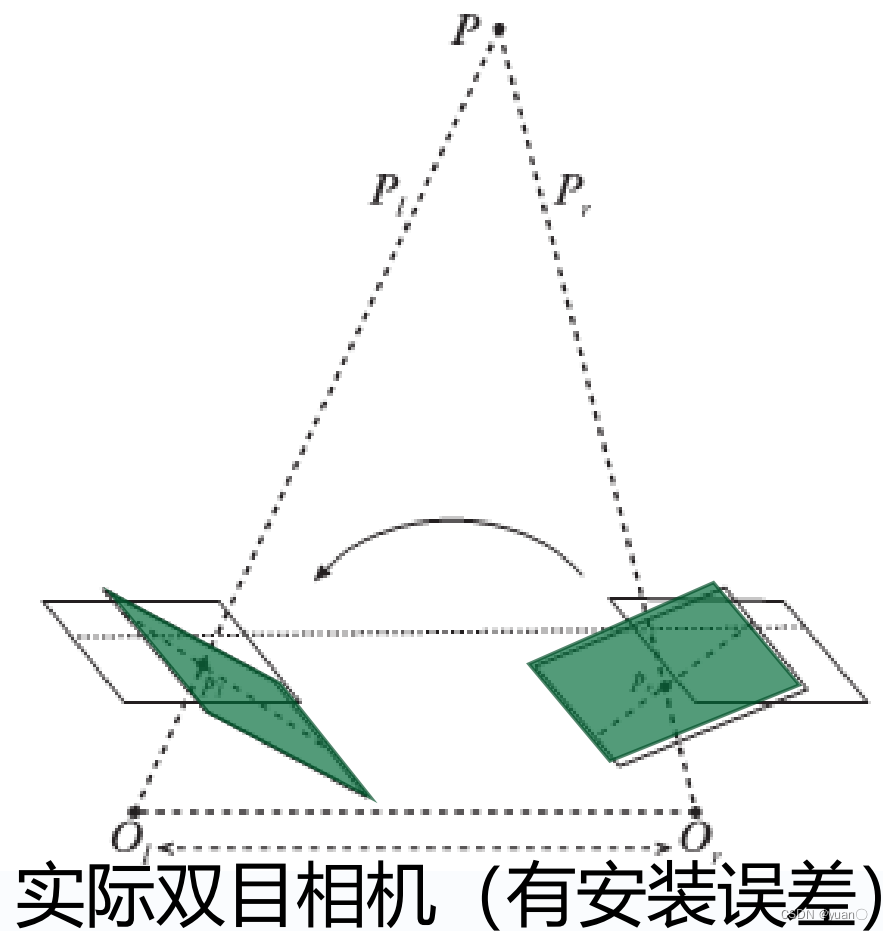双面相机两相机间的角度可能存在偏差，因此测距原理
z
=
f
b
u
L
−
u
R
z = \frac{{fb}}{{{u_L} - {u_R}}}
z=uL−uRfb不再适用，需要进行重新标定。具体标定对象则是两相机之间的相对旋转矩阵与平移向量。
除此之外，两相机之间的相对距离也可能有安装误差，同样需要标定。把左右相机的图像在水平方向严格对齐，对原始图像进行消除畸变，再进行图像校正与图像裁剪，最后就能得到校正后的图像。
2.5 俯视图转化标定——逆透视变换
逆透视变换，英文为IPM (Inverse Perspective Mapping)
原理：根据图片坐标与世界坐标的关系，将图片像素
u
v
uv
uv对应到路面
x
y
xy
xy
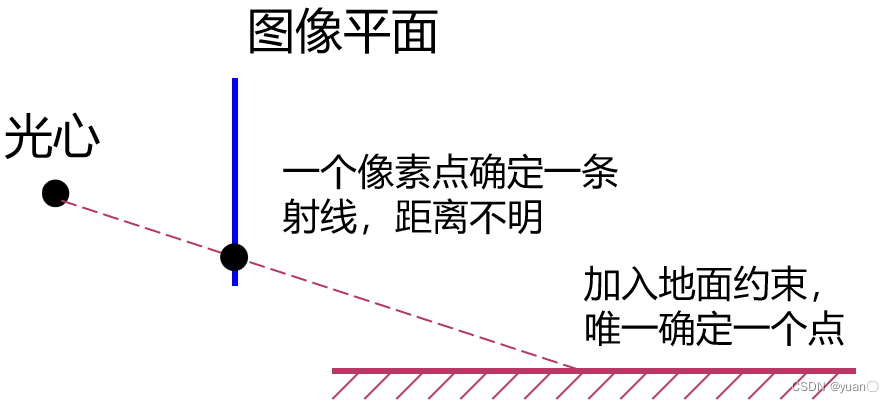
难点：一般来说，图片没有距离尺度信息，一个像素点确定一条射线而不能确定是哪个点
解决办法：假设地面平坦且高度已知
（
z
=
0
）
（z=0）
（z=0），就等于将世界坐标降维到二维，实现
u
v
uv
uv与
x
y
xy
xy的一一对应。
接下来进行公式推导：
- 相机成像公式，内参外参可以合并为一个3乘4矩阵 M M M Z c [ μ ν 1 ] = [ f x 0 u 0 0 0 f y v 0 0 0 0 1 0 ] [ R 3 × 3 T 3 × 1 0 1 ] [ x y z 1 ] = [ M 1 M 2 M 3 M 4 M 5 M 6 M 7 M 8 M 9 M 10 M 11 M 12 ] ⋅ [ x y z 1 ] \begin{array}{c}{Z_c}\left[ {\begin{array}{ccccccccccccccc}\mu \\nu \1\end{array}} \right] = \left[ \begin{array}{l}\begin{array}{ccccccccccccccc}{{f_x}}&0&{{u_0}}&0\end{array}\\begin{array}{ccccccccccccccc}0&{{f_y}}&{{v_0}}&0\end{array}\\begin{array}{ccccccccccccccc}0&0&1&0\end{array}\end{array} \right]\left[ {\begin{array}{ccccccccccccccc}{{R_{{\rm{3}} \times 3}}}&{{T_{3 \times 1}}}\0&1\end{array}} \right]\left[ \begin{array}{l}x\y\z\1\end{array} \right]\ = \left[ {\begin{array}{lllllllllllllll}{\begin{array}{ccccccccccccccc}{{M_1}}&{{M_2}}&{{M_3}}&{{M_4}}\end{array}}\{\begin{array}{ccccccccccccccc}{{M_5}}&{{M_6}}&{{M_7}}&{{M_8}}\end{array}}\{\begin{array}{ccccccccccccccc}{{M_9}}&{{M_{10}}}&{{M_{11}}}&{{M_{12}}}\end{array}}\end{array}} \right] \cdot \left[ {\begin{array}{ccccccccccccccc}x\y\z\1\end{array}} \right]\end{array} Zcμν1=fx0u000fyv000010[R3×30T3×11]xyz1=M1M2M3M4M5M6M7M8M9M10M11M12⋅xyz1
- 假设地面平坦，令 z = 0 z=0 z=0，就可以去掉 M M M的第三列，两侧左乘 M − 1 M^{−1} M−1，并将 Z c Z_c Zc移到右侧，记 w = 1 / Z c w=1/Z_c w=1/Zc， P = M − 1 P=M^{−1} P=M−1 Z c [ μ ν 1 ] = [ M 1 M 2 M 4 M 5 M 6 M 8 M 9 M 10 M 12 ] [ x y 1 ] {Z_c}\left[ {\begin{array}{ccccccccccccccc}\mu \\nu \1\end{array}} \right] = \left[ {\begin{array}{ccccccccccccccc}{{M_1}}&{{M_2}}&{{M_4}}\{{M_5}}&{{M_6}}&{{M_8}}\{{M_9}}&{{M_{10}}}&{{M_{12}}}\end{array}} \right]\left[ {\begin{array}{ccccccccccccccc}x\y\1\end{array}} \right] Zcμν1=M1M5M9M2M6M10M4M8M12xy1 [ p 11 ′ p 12 ′ p 13 ′ p 12 ′ p 22 ′ p 23 ′ p 13 ′ p 23 ′ p 33 ′ ] [ μ ν 1 ] = w [ x y 1 ] \left[ {\begin{array}{ccccccccccccccc}{{p_{11}}^\prime }&{{p_{12}}^\prime }&{{p_{13}}^\prime }\{{p_{12}}^\prime }&{{p_{22}}^\prime }&{{p_{23}}^\prime }\{{p_{13}}^\prime }&{{p_{23}}^\prime }&{{p_{33}}^\prime }\end{array}} \right]\left[ {\begin{array}{ccccccccccccccc}\mu \\nu \1\end{array}} \right] = w\left[ {\begin{array}{ccccccccccccccc}x\y\1\end{array}} \right] p11′p12′p13′p12′p22′p23′p13′p23′p33′μν1=wxy1
- 归一化：将P中各元素除以 p 33 ′ p_{33}′ p33′， w w w也除以 p 33 ′ p_{33}′ p33′，重新整理得 [ p 11 p 12 p 13 p 12 p 22 p 23 p 13 p 23 1 ] [ μ ν 1 ] = w ′ [ x y 1 ] \left[ {\begin{array}{ccccccccccccccc}{{p_{11}}}&{{p_{12}}}&{{p_{13}}}\{{p_{12}}}&{{p_{22}}}&{{p_{23}}}\{{p_{13}}}&{{p_{23}}}&1\end{array}} \right]\left[ {\begin{array}{ccccccccccccccc}\mu \\nu \1\end{array}} \right] = w'\left[ {\begin{array}{ccccccccccccccc}x\y\1\end{array}} \right] p11p12p13p12p22p23p13p231μν1=w′xy1
记点
A
A
A在图片中坐标（
u
A
,
v
A
u_A, v_A
uA,vA),真实世界坐标（
x
A
,
y
A
x_A, y_A
xA,yA）,则有
[
w
x
A
w
y
A
w
]
=
[
p
11
p
12
p
13
p
12
p
22
p
23
p
13
p
23
1
]
[
u
A
ν
A
1
]
\left[ {\begin{array}{ccccccccccccccc}{w{x_A}}\\{w{y_A}}\\w\end{array}} \right] = \left[ {\begin{array}{ccccccccccccccc}{{p_{11}}}&{{p_{12}}}&{{p_{13}}}\\{{p_{12}}}&{{p_{22}}}&{{p_{23}}}\\{{p_{13}}}&{{p_{23}}}&1\end{array}} \right]\left[ {\begin{array}{ccccccccccccccc}{{u_A}}\\{{\nu _A}}\\1\end{array}} \right]
wxAwyAw=p11p12p13p12p22p23p13p231uAνA1 用第三行消去
w
w
w，得
x
A
=
p
11
u
A
+
p
12
v
A
+
p
13
p
31
u
A
+
p
32
v
A
+
1
{x_A} = \frac{{{p_{11}}{u_A} + {p_{12}}{v_A} + {p_{13}}}}{{{p_{31}}{u_A} + {p_{32}}{v_A} + 1}}
xA=p31uA+p32vA+1p11uA+p12vA+p13
y
A
=
p
21
u
A
+
p
22
v
A
+
p
23
p
31
u
A
+
p
32
v
A
+
1
{y_A} = \frac{{{p_{21}}{u_A} + {p_{22}}{v_A} + {p_{23}}}}{{{p_{31}}{u_A} + {p_{32}}{v_A} + 1}}
yA=p31uA+p32vA+1p21uA+p22vA+p23 矩阵方程形成以
p
i
j
p_{ij}
pij作为未知数的2个方程
对
B
C
D
BCD
BCD重复上述操作，形成8个方程，就能求解出全部8个未知数
声明
本人所有文章仅作为自己的学习记录，若有侵权，联系立删。本系列文章主要参考了清华大学、北京理工大学、哈尔滨工业大学、深蓝学院、百度Apollo等相关课程。
本文转载自: https://blog.csdn.net/sinat_52032317/article/details/128762095
版权归原作者 yuan〇 所有， 如有侵权，请联系我们删除。
版权归原作者 yuan〇 所有， 如有侵权，请联系我们删除。