2022年第二届长三角高校数学建模竞赛B题经验、论文、代码展示

2022年第二届长三角高校数学建模竞赛B题经验、论文、代码展示

1、题目要求
其中数据
附件一数据（截图部分）：
附件二数据（部分截图）：

在这里插入代码片

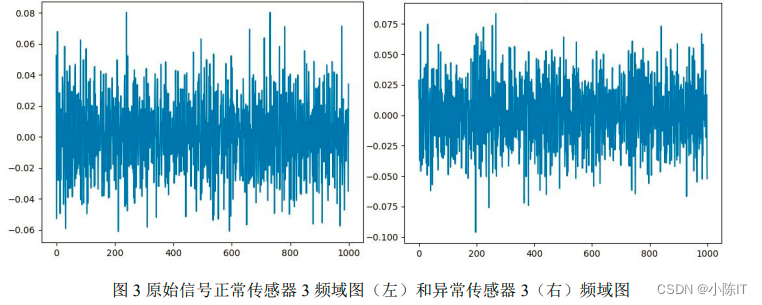
问题一到问题四的思路：
针对问题一，对附件 1 中的 5 个表单的四个传感器数据进行分析，提取相关特征。
研究发现 VMD 方法在可以避免模态混叠问题。VMD 的低频分量，更容易表达出振动信号故障波动的大趋势。首先，对每个状态，以每 1000 条记录构造样本数据。通过绘制 5个状态下的样本时域图，观察波形的整体情况。其次，对样本数据进行 VMD 变分模态提取四个 IMF 分量。从振动信号的时域特征、频域特征和能量特征三个方面出发，对每个IMF 分量提取构建了均值、峰值、中心频率等 24 个特征，并构建对应特征向量，建立对应的数学公式和计算过程。最后，根据优化组合，得到频域+能量所构建的特征向量可有效区分正常状态和异常状态。差异结果见表 2、3。
针对问题二，要求检测齿轮箱是否故障。首先，在问题一所求 IMF 模态分量的基础上，使用 SVD 降噪重构，对每个 IMF 变量，提取时域、频域、能量域的特征，优化组合，选取频域+能量域构建特征向量。其次，通过构建基于 VMD 的齿轮箱故障检测模型对各个状态的振动信号进行判断。构造样本数据和二分类的标签，以 8:2 划分训练集和测试集，采用 SVM 作为分类器，以准确率为评价指标，进行故障检测。最后得出该模型对振动信号故障检测准确率为 100%。
针对问题三，要求判断齿轮箱具体故障类型。具体故障类型有正常、故障 1、故障2、故障 3、故障 4 共 5 种类型。构造样本数据和五分类的标签，以 8:2 划分训练集和测试集，SVM 作为分类器，以准确率为评价指标，进行故障判断。最后得出该模型对振动信号故障判断准确率为 96.7%。
针对问题四，结合问题二、问题三的模型对测试数据进行检测和判断分析。考虑到
其他故障存在的可能性，通过设置其他类阈值来对检测和判断模型进行修正。当检测和
判断模型对所预测类型的最大概率不大于其他类阈值时，判断为其他故障。最终的测试
数据的诊断结果表如表 4 所示。

问题一代码
`import numpy as np
import matplotlib.pyplot as plt
import xlrd as xd
from vmdpy import VMD
from scipy.fftpack import fft
def xls2npy():'''转换数据格式
:return:'''for i in [0,1]:if i ==0:
curTablePath ="train"else:
curTablePath ="test" # 加载数据
tables = xd.open
_workbook("../data/xls/"+curTablePath+".xls")
sheetNames = tables.sheet
_names()
dict ={}for i in range(len(sheetNames)):
curSheetName = sheetNames[i]
curSheet = tables.sheet
_by_name(curSheetName)
ncols = curSheet.ncols
# 按列加载每一个 sheet 的每列数据
curSheetData =[]
# 去除第一列，即 No 列
for j in range(1, ncols):
curCol = curSheet.col
_values(j)
# 去除第一行
curCol = curCol[1:-1]
curSheetData.append(curCol)
# 对每列进行最大最小归一化，以去除数值过大的影响
curSheetData = np.vstack([item for item in curSheetData])
# 转为（29339，4）
curSheetData = curSheetData.transpose()
dict[curSheetName]= curSheetData
np.save("../data/npy/"+curTablePath+"/dict.npy",dict)
np.save("../data/npy/"+curTablePath+"/sheetNames.npy",sheetNames)print("_")
def showSensorFeatures():'''对训练集数据进行 VMD、SVD 后特征提取
:return:''' basePath ="../data/npy/" dict = np.load(basePath +"train/dict.npy", allow
_pickle=True).item()
# 所有状态的传感器 1
gearBoxs =['gearbox00','gearbox10','gearbox20','gearbox30','gearbox40']for i in range(len(gearBoxs)):
curGearBoxName = gearBoxs[i]
# 正常状态传感器 1
# 每一千条计算一个样本特征
# 记录当前状态下的四个传感器的特征向量
samplesFeaturesChain =[]for j in range(4):
curGearBoxData = dict[curGearBoxName][:, j]
size = curGearBoxData.shape[0]
curNum =0
samplesFeatures =[]
curLeft = size
data1 = curGearBoxData[curNum:curNum +1000]
curNum +=1000
curLeft -=1000
u, u
_hat, omega =vmd(data1)
# 对每个分量进行 svd 去噪
for i in range(len(u)):
curIMF = u[i]
# 对每个分量进行去噪
curIMF =svd(curIMF)
u[i]= curIMF
# 得到每个模态特征向量
curUIMFFeas =calIndicator(u)
# 将当前传感器前 1000 条数据作为一个记录，画出中心模态
dataPlot(data1,4,u)
def vmd(data1):'''计算当前传感器数据 data1 的四个本征模态分量
:param data1: 传感器数据
:return: 模态分量 u
''' alpha =7000 # moderate bandwidth constraint
tau =0. # noise-tolerance(no strict fidelity enforcement)
K =4 # 3 modes
DC =0 # no DC part imposed
init =1 # initialize omegas uniformly
tol =1e-716#u是分量
u, u
_hat, omega =VMD(data1, alpha, tau, K, DC, init, tol)return u, u
_hat, omega
def svd(u
_IMFi):''' 对某个状态的某个 IMF 分量 u 进行奇异值去噪
:param u
_IMFi::return:''' # series = np.load('../data/npy/train/box00/u.npy')[0,:1000]
series = u
_IMFi
#step1 嵌入
windowLen =20 # 嵌入窗口长度
seriesLen =len(series) # 序列长度
K = seriesLen - windowLen +1
X = np.zeros((windowLen, K))for i in range(K):
X[:, i]= series[i:i + windowLen]#step2: svd 分解， U 和 sigma 已经按升序排序
U, sigma, VT = np.linalg.svd(X, full
_matrices=False)for i in range(VT.shape[0]):
VT[i,:]*= sigma[i]
A = VT
# 重组
rec = np.zeros((windowLen, seriesLen))for i in range(windowLen):for j in range(windowLen -1):for m in range(j +1):
rec[i, j]+= A[i, j - m]* U[m, i]
rec[i, j]/=(j +1)for j in range(windowLen -1, seriesLen - windowLen +1):for m in range(windowLen):
rec[i, j]+= A[i, j - m]* U[m, i]
rec[i, j]/= windowLen
for j in range(seriesLen - windowLen +1, seriesLen):for m in range(j - seriesLen + windowLen, windowLen):
rec[i, j]+= A[i, j - m]* U[m, i]
rec[i, j]/=(seriesLen - j)
rrr = np.sum(rec[:2,:], axis=0) # 选择重构的部分，这里选了前三个
return rrr
if
__name
__ == '__main
__':
# 将 xls 文件转化为 npy 文件
xls2npy()
# 展示特征向量
showSensorFeatures()`

问题二代码：
import numpy as np
from sklearn.svm import SVC
from sklearn.model
_selection import train
_test
_split
import scipy.stats
def getSensorFeature():'''构造传感器的特征向量
:return:''' basePath ="../data/npy/" # 训练数据
dict = np.load(basePath +"train/dict.npy", allow
_pickle=True).item()
# 测试数据
#dict= np.load(basePath +"test/dict.npy", allow
_pickle=True).item()
# 所有状态的传感器 1
gearBoxs =['gearbox00','gearbox10','gearbox20','gearbox30','gearbox40']
testBoxs =['test1','test2','test3','test4','test5','test6','test7','test8','test9','test10','test11','test12']
samplesFeaturesDict ={}for i in range(len(gearBoxs)):
curGearBoxName = gearBoxs[i]
# 正常状态传感器 1
# 每一千条计算一个样本特征
curGearBoxData = dict[curGearBoxName]
# 记录当前状态下的四个传感器的特征向量
samplesFeaturesChain =[]for j in range(4):
curGearBoxData = dict[curGearBoxName][:,j]
size = curGearBoxData.shape[0]
curNum =0
samplesFeatures =[]
curLeft = size
while(curLeft>0):
# 得到当前 1000 条数据
steps =1000if curLeft<=1000:
steps = curLeft
data1 = curGearBoxData[curNum:curNum+steps]
curNum+=1000
curLeft-=1000
u, u
_hat, omega =vmd(data1)
# 对每个分量进行 svd 去噪
# 若需要原始信号的频谱图，则注释下面的 for 循环
for i in range(len(u)):
curIMF = u[i]
# 对每个分量进行去噪
curIMF =svd(curIMF)
u[i]=curIMF
# 得到每个模态特征向量
curUIMFFeas =calIndicator(u)
samplesFeatures.append(curUIMFFeas)
# (30,52)
samplesFeatures =
np.reshape(samplesFeatures,(len(samplesFeatures),samplesFeatures[0].shape[0]))
samplesFeaturesChain.append(samplesFeatures)print(".")
# 需要得到 30,52*4 的数据
samplesFeaturesChain = np.hstack([item for item in samplesFeaturesChain])
samplesFeaturesDict[curGearBoxName]= samplesFeaturesChain
# 当需要训练集数据时，消注释这条
np.save('../data/npy/train/sampelsFeaturesDict.npy', samplesFeaturesDict)
# 当需要测试集数据时，消注释这条
#np.save('../data/npy/test/sampelsFeaturesDict.npy', samplesFeaturesDict)
# 特征提取类
class Fea
_Extra():
def
__init
__(self, Signal, Fs =25600):
self.signal = Signal
self.Fs = Fs
def Time
_fea(self):""" 提取时域特征 11 类
"""
signal
_ = self.signal
N =len(signal
_)
y = signal
_
# 1
_均值（平均幅值）
t
_mean
_1 = np.mean(y)
# 3
_方根幅值
t
_fgf
_3 =((np.mean(np.sqrt(np.abs(y)))))**2
# 4
_RMS 均方根
t
_rms
_4 = np.sqrt((np.mean(y**2)))
# 5
_峰峰值
t
_pp_5 =0.5*(np.max(y)-np.min(y))
# 6
_偏度 skewness
t
_skew
_6 = scipy.stats.skew(y)
# 7
_峭度 Kurtosis
t
_kur
_7 = scipy.stats.kurtosis(y)
# 8
_峰值因子 Crest Factor
t
_cres
_8 = np.max(np.abs(y))/t
_rms
_4
# 9
_裕度因子 Clearance Factor
t
_clear
_9 = np.max(np.abs(y))/t
_fgf
_3
# 10
_波形因子 Shape fator
t
_shape
_10 =(N * t
_rms
_4)/(np.sum(np.abs(y)))
# 11
_脉冲指数 Impulse Fator
t
_imp_11 =( np.max(np.abs(y)))/(np.mean(np.abs(y)))
t
_max
_12 = np.max(y)
t
_fea = np.array([t
_mean
_1, t
_rms
_4, t
_pp_5, t
_skew
_6, t
_kur
_7, t
_cres
_8, t
_clear
_9, t
_shape
_10, t
_imp_11,t
_max
_12])return t
_fea
def Fre
_fea(self):""" 提取频域特征 13 类
:param signal
_::return:"""
signal
_ = self.signal
L =len(signal
_)
PL =abs(np.fft.fft(signal
_ / L))[:int(L /2)]
PL[0]=0
f = np.fft.fftfreq(L,1/ self.Fs)[:int(L /2)]
x = f
y = PL
K =len(y)
f
_12 = np.mean(y)
f
_13 = np.var(y)
f
_14 =(np.sum((y - f
_12)**3))/(K *((np.sqrt(f
_13))**3))
f
_15 =(np.sum((y - f
_12)**4))/(K *((f
_13)**2))
f
_16 =(np.sum(x * y))/(np.sum(y))
f
_17 = np.sqrt((np.mean(((x- f
_16)**2)*(y))))
f
_18 = np.sqrt((np.sum((x**2)*y))/(np.sum(y)))
f
_19 = np.sqrt((np.sum((x**4)*y))/(np.sum((x**2)*y)))
f
_20 =(np.sum((x**2)*y))/(np.sqrt((np.sum(y))*(np.sum((x**4)*y))))
f
_21 = f
_17/f
_16
f
_22 =(np.sum(((x - f
_16)**3)*y))/(K *(f
_17**3))
f
_23 =(np.sum(((x - f
_16)**4)*y))/(K *(f
_17**4))
f
_fea = np.array([f
_12, f
_13, f
_14, f
_15, f
_16, f
_17, f
_18, f
_19, f
_20, f
_21, f
_22, f
_23])return f
_fea
def calIndicator(u):''' :param u: 某个状态下模态分量的集合
:return: 某个状态对应模态分量的特征变量
''' Elist =[]
timeFeas =[]
freqFeas =[]
# 对每一个分量机 IMFi 计算时域、频域、能量域的特征值
for i in range(u.shape[0]):
curU = u[i,:]
# 计算能量值
E =0for i in curU:
E +=(i * i)
Elist.append(E)
# 计算时域值
time
_fea = Fea
_Extra(curU).Time
_fea()
# 计算频域值
freq_fea = Fea
_Extra(curU).Fre
_fea()
timeFeas.append(time
_fea)
freqFeas.append(freq_fea)
totalE = np.sum(Elist)
Elist = Elist / totalE
# 时域特征、频域特征、能量值
IMFFeas =[]for i in range(u.shape[0]):
curIMFFeatures =[]
curTimeFea = timeFeas[i]
curFreqFea = freqFeas[i]
curEnergyMark = Elist[i]#curIMFFeatures.append(curTimeFea)
# 目前实现频域+能量的特征
curIMFFeatures.append(curFreqFea)
curIMFFeatures.append(curEnergyMark)
curIMFFeatures = np.hstack([item for item in curIMFFeatures])
IMFFeas.append(curIMFFeatures)
IMFFeas = np.hstack([item for item in IMFFeas])return IMFFeas
def structDataSet(sampleDict):'''根据字典，重构数据集，将其转化为（N,208)的形式
:param sampleDict::return:''' dataSet =[]for gearBox in sampleDict:
curData = sampleDict[gearBox]
dataSet.append(curData)
dataSet = np.reshape(dataSet,(len(dataSet)*dataSet[0].shape[0],dataSet[0].shape[1]))return dataSet
def normalization(trainData,testData=None):'''对训练集和测试集进行归一化
:param trainData: 训练集
:param testData: 测试集
:return:''' normalization
_part1(trainData)
maxList = np.load('../../data/npy/train/maxList.npy')
minList = np.load('../../data/npy/train/minList.npy')for i in range(trainData.shape[0]):
curRowData = trainData[i]
curRowData =(curRowData - minList)/(maxList-minList)
trainData[i]= curRowData
if testData is not None:for i in range(testData.shape[0]):
curRowData = testData[i]
curRowData =(curRowData - minList)/(maxList - minList)
testData[i]= curRowData
if testData is None:return trainData,""else:return trainData,testData
def findException(dataSet,gearBoxs):'''建立故障检测模型
:param dataSet::param gearBoxs::return:''' labels =[]
# 设置数据标签
for i in range(len(gearBoxs)):if i not in [0]:
curLabel = np.repeat(1,30)else:
curLabel = np.repeat(i,30)
labels.append(curLabel)
# 将标签合并为一维数据
labels = np.hstack([item for item in labels])
x
_train, x
_test, y_train, y_test = train
_test
_split(dataSet, labels, random
_state=9, train
_size=0.8, stratify=labels)
clf =SVC(kernel='linear', probability=True)
clf.fit(x
_train, y_train)
# 计算准确率
score = clf.score(x
_test,y_test)print(score)if
__name
__ == '__main
__':
# 获得传感器数据的特征向量
getSensorFeature()
sampleDict = np.load('../../data/npy/train/sampelsFeaturesDict.npy',allow
_pickle=True).item()
# 所有状态的传感器 1
gearBoxs =['gearbox00','gearbox10','gearbox20','gearbox30','gearbox40']
# 将字典数据转化为矩阵
trainDataSet =structDataSet(sampleDict)
# 对训练数据和测试数据进行归一化
trainData,testData =normalization(trainDataSet,testDataSet)
# 建立故障检测模型
findException(trainData,gearBoxs)

问题三、问题四代码
import numpy as np
from sklearn.svm import SVC
from sklearn.model
_selection import train
_test
_split
def judgeException(dataSet,testData,gearBoxs):''' 建立故障判断模型
:param dataSet::param testData::param gearBoxs::return:''' labels =[]
# 设置数据标签
for i in range(len(gearBoxs)):
curLabel = np.repeat(i,30)
labels.append(curLabel)
# 将标签合并为一维数据
labels = np.hstack([item for item in labels])
x
_train, x
_test, y_train, y_test = train
_test
_split(dataSet, labels, random
_state=9, train
_size=0.8, stratify=labels)
clf =SVC(kernel='linear', probability=True)
clf.fit(x
_train, y_train)
pred
_pro = clf.predict
_proba(testData)
pred
_label = clf.predict(testData)for i in range(len(pred
_pro)):
curPro = pred
_pro[i]
curMaxPro = np.max(curPro)if curMaxPro <=0.4:
pred
_label[i]=5print(pred
_label)
excpName =['正常','异常 1','异常 2','异常 3','异常 4','其他异常',]
pred
_Names =[]for i in range(len(pred
_label)):
pred
_Names.append(excpName[pred
_label[i]])print(pred
_Names)if
__name
__ == '__main
__':
sampleDict = np.load('../../data/npy/train/sampelsFeaturesDict.npy',allow
_pickle=True).item()
# 所有状态的传感器 1
gearBoxs =['gearbox00','gearbox10','gearbox20','gearbox30','gearbox40']
# 将字典数据转化为矩阵
trainDataSet =structDataSet(sampleDict)
testDict = np.load("../../data/npy/test/sampelsFeaturesDict.npy",allow
_pickle=True).item()
# 将字典数据转化为矩阵
testDataSet =structDataSet(testDict)
# 对训练数据和测试数据进行归一化
trainData,testData =normalization(trainDataSet,testDataSet)
# 建立故障判断模型
judgeException(trainData,testData,gearBoxs)