Haar级联分类器概述
—— 才疏学浅, 难免有错误和遗漏, 欢迎补充和勘误.
Haar级联分类器是基于Haar-like特征,运用积分图加速计算,并用Adaboost训练的强分类器级联的方法来进行人脸检测。
目前常用Haar-like特征的分类有:
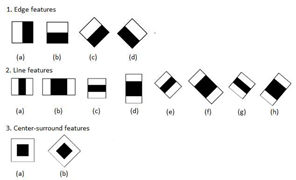
图1. Haar-like特征分类
首先定义每个Haar-like特征的特征值 f i f_i fi为: featurevalue i = {i}= i= weight white ∑ p ∈ wite p \sum{p \in \text { wite }} p ∑p∈ wite p - weightblack ∑ p Eblack p \sum_{p \text { Eblack }} p ∑p Eblack p 即 f i f_i fi=白色区域像素-黑色区域像素,weight为权重值,其是为了白、黑两种矩形区域的像素数目一致,保证在灰度绝对均匀的地方其特征值是0。
Haar-like特征的值经过运算可以反映该区域的灰度变化情况,将一副输入图像的每一个区域也做类似的运算后与训练集中图像的Haar-like特征值对比,如图2所示,根据生活实际我们有以下常识:在人脸上鼻梁两边部位的颜色比鼻梁处更深,两个眼睛部位的颜色比旁边脸颊处更深等,所以可以据此判断输入图像是否具有人脸特征。
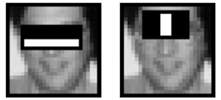
图2. Haar-like特征在人脸图中的应用
特征模板经过平移、伸缩变换得到一系列新的矩形特征。矩形特征根据其类型、位置和大小的不同,可以在一副图像中可以生成非常多的矩形特征从而增大了计算压力,所以需要运用积分图的方法来提高特征值的计算效率。
积分图的构造方式是:位于图像 ( i , j ) (i,j) (i,j)处的积分图 i i ( i , j ) ii(i,j) ii(i,j)是该处左上角方向所有像素 f ( k , l ) f(k,l) f(k,l)的和:integral_image ( i , j ) = i i ( i , j ) = ∑ k ≤ i , l ≤ j f ( k , l ) (i, j)=i i(i, j)=\sum_{k \leq i, l \leq j} f(k, l) (i,j)=ii(i,j)=∑k≤i,l≤jf(k,l)
积分图在图像各个点的处上储存了其左上角所有像素的和,下面是对图像中某一区域运用积分图计算Haar-like特征来得到其特征值:
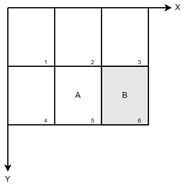
图3. 矩形特在坐标中的表示
区域A的像素值为:
i
i
(
5
)
+
i
i
(
1
)
−
i
i
(
2
)
−
i
i
(
4
)
ii(5) + ii(1) - ii(2) - ii(4)
ii(5)+ii(1)−ii(2)−ii(4),
区域B的像素值为:
i
i
(
6
)
+
i
i
(
2
)
−
i
i
(
5
)
−
i
i
(
3
)
ii(6) + ii(2) - ii(5) - ii(3)
ii(6)+ii(2)−ii(5)−ii(3)。
该矩形特征的特征值为:
i
i
(
5
)
+
i
i
(
1
)
−
i
i
(
2
)
−
i
i
(
4
)
−
[
i
i
(
6
)
+
i
i
(
2
)
−
i
i
(
5
)
−
i
i
(
3
)
]
=
[
i
i
(
5
)
−
i
i
(
4
)
]
+
[
i
i
(
3
)
−
i
i
(
2
)
]
−
[
i
i
(
2
)
−
i
i
(
1
)
]
−
[
i
i
(
6
)
−
i
i
(
5
)
]
\begin{array}{l} ii(5) + ii(1) - ii(2) - ii(4) - \left[ {ii(6) + ii(2) - ii(5) - ii(3)} \right]\\ = \left[ {ii(5) - ii(4)} \right] + \left[ {ii(3) - ii(2)} \right] - \left[ {ii(2) - ii(1)} \right] - \left[ {ii(6) - ii(5)} \right] \end{array}
ii(5)+ii(1)−ii(2)−ii(4)−[ii(6)+ii(2)−ii(5)−ii(3)]=[ii(5)−ii(4)]+[ii(3)−ii(2)]−[ii(2)−ii(1)]−[ii(6)−ii(5)]
对于 m m m个正、负样本图像中的某个固定特征fi计算出每张图像该特征的特征值,将计算出的 m m m个特征值进行排序和打标识,然后根据上节(基于AdaBoost级联分类器的人脸/眼睛位置检测算法概述)1.中的原理取到最优阈值并获得该特征下的最优弱分类器,根据上节2.和3.原理来训练出该特征的强分类器,最终通过级联的方式获得Haar级联分类器。下图为运用Haar级联分类器来检测人脸的过程:
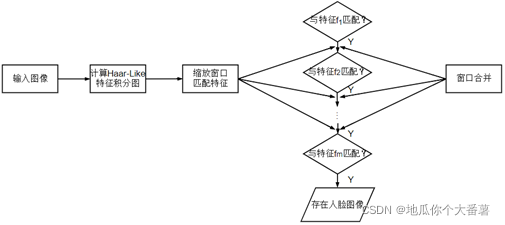
图4. Haar级联分类器检测人脸过程
版权归原作者 地瓜你个大番薯 所有, 如有侵权,请联系我们删除。