自动驾驶中激光雷达如何检测障碍物
Reference:
- 高翔，张涛 《视觉SLAM十四讲》
- 自动驾驶中激光雷达检测障碍物理论与实践
激光雷达是利用激光束来感知三维世界，通过测量激光返回所需的时间输出为点云。它集成在自动驾驶、无人机、机器人、卫星、火箭等许多领域。
1. 介绍
1.1 激光雷达-一种三维激光传感器
激光雷达传感器利用光原理进行工作，激光雷达代表光探测和测距。它们可以探测到 300m 以内的障碍物，并准确估计它们的位置。在自动驾驶汽车中，这是用于位置估计的最精确的传感器。
激光雷达传感器由两部分组成：激光发射（顶部）和激光接收（底部）。发射系统的工作原理是利用多层激光束，层数越多，激光雷达就越精确。层数越多，传感器就越大。激光被发射到障碍物并反射，当这些激光击中障碍物时，它们会产生一组点云，传感器与飞行时间（TOF）进行工作，从本质上说，它测量的是每束激光反射回来所需的时间。如下图：
当激光雷达的质量和价格非常高时，激光雷达是可以创建丰富的三维环境，并且每秒最多可以发射200万个点。点云表示三维世界激光雷达传感器获得每个撞击点的精确
(
X
,
Y
,
Z
)
(X, Y, Z)
(X,Y,Z)位置。
激光雷达传感器可以是固态的，也可以是旋转的，固态激光雷达将把检测的重点放在一个位置上，并提供一个覆盖范围（比如FOV为90°）。在后一种情况下，它将围绕自身旋转，并提供360°旋转。在这种情况下，一般把它放在设备顶上，以提高能见度。
激光雷达很少用作独立传感器。它们通常与相机或雷达结合在一起，这一过程称为传感器融合。融合过程可分为早期融合和后期融合。早期融合是指点云与图像像素融合，后期融合是指单个检测物的融合。
1.2 激光雷达的优缺点？
缺点：
- 激光雷达不能直接估计速度。他们需要计算两个连续测量值之间的差值。
- 激光雷达在恶劣的天气条件下工作不好。在有雾或者下雨的情况下，激光会击中它，使场景变得混乱。
- 激光雷达的价格虽然在下降，但仍然很高。
优点：
- 激光雷达可以精确地估计障碍物的位置。到目前为止，还没有更准确的方法。
- 激光雷达处理点云。如果我们看到车辆前方的点云，即使障碍物检测系统没有检测到任何东西，我们也可以及时停车。这是一个很大的安全保证，车辆将不仅依赖于图像的神经网络和概率问题。
1.3 基于激光雷达如何进行障碍物检测？
激光雷达进行障碍物的步骤通常分为 4 个步骤：
- 点云处理
- 点云分割
- 障碍聚类
- 边界框拟合
1.4 点云处理难点
- 稀疏的；
- 不规则----搜索邻居比较困难；
- 缺乏纹理信息；
- 无序的----深度学习很困难； [ x 1 y 1 z 1 x 2 y 2 z 2 ⋮ ⋮ ⋮ x N y N z N ] = [ x 2 y 2 z 2 x 1 y 1 z 1 ⋮ ⋮ ⋮ x k y k z k ] \left[\begin{array}{ccc}x_{1} & y_{1} & z_{1} \ x_{2} & y_{2} & z_{2} \ \vdots & \vdots & \vdots \ x_{N} & y_{N} & z_{N}\end{array}\right]=\left[\begin{array}{ccc}x_{2} & y_{2} & z_{2} \ x_{1} & y_{1} & z_{1} \ \vdots & \vdots & \vdots \ x_{k} & y_{k} & z_{k}\end{array}\right] ⎣⎢⎢⎢⎡x1x2⋮xNy1y2⋮yNz1z2⋮zN⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡x2x1⋮xky2y1⋮ykz2z1⋮zk⎦⎥⎥⎥⎤如上面的行换了，表达的还是同一个物体。对于深度学习而言，输入进去的矩阵是不一样的就会产生不同的输出，但是我们希望输出是一样的。
- 旋转同变性/不变性：我们旋转一些点，它的坐标是不一样的，但是它还是同一个物体。
2. 点云处理
2.1 点云处理-体素网格
为了处理点云，我们可以使用最流行的库 PCL(point cloud library)。它在 Python 中可用，但是在 C++ 中使用它更为合理，因为语言更适合机器人学。它也符合 ROS(机器人操作系统)。PCL 库可以完成探测障碍物所需的大部分计算，从加载点到执行算法。这个库相当于 OpenCV 的计算机视觉。因为激光雷达的输出很容易达到每秒 100000 个点，所以我们需要使用一种称为体素网格的方法来对点云进行下采样。
2.1.1 什么是体素网格？
体素网格是一个三维立方体，通过每个立方体只留下一个点来过滤点云。立方体越大，点云的最终分辨率越低。最终，我们可以将点云的采样从几万点减少到几千点。
滤波完成后我们可以进行的第二个操作是 ROI(感兴趣区域) 的提取，我们只需删除不属于特定区域的每一些点云数据，例如左右距离 10m 以上的点云，前后超过 100m 的点云都通过滤波器滤除。现在我们有了降采样并滤波后的点云了，此时可以继续进行点云的分割、聚类和边界框实现。
3 三维点云的分割
3.1 RANSAC
点云分割任务是将场景与其中的障碍物分离开来，其实就是地面的分割。一种非常流行的分割方法称为 RANSAC(Random Sample consenses)。该算法的目标是识别一组点中的异常值。点云的输出通常表示一些形状。有些形状表示障碍物，有些只是表示地面上的反射。RANSAC 的目标是识别这些点，并通过拟合平面或直线(拟合的是地面)将它们与其他点分开。
为了拟合直线，我们可以考虑线性回归。但是有这么多的异常值，线性回归会试图平均结果，而得出错误的拟合结果，与线性回归相反，这里的 RANSAC 算法将识别这些异常值，且不会拟合它们。
如上图所示我们可以将这条线视为场景的目标路径（即道路），而孤立点则是障碍物。
3.1.1 RANSAC 的实现
过程如下：
- 随机选取2个点
- 将线性模型拟合到这些点计算每隔一点到拟合线的距离。如果距离在定义的阈值距离公差范围内，则将该点添加到内联线列表中。
因此需要算法一个参数：距离阈值。
最后选择内点最多的迭代作为模型；其余的都是离群值。这样，我们就可以把每一个内点视为道路的一部分，把每一个外点视为障碍的一部分。RANSAC应用在3D点云中。在这种情况下，3个点之间的构成的平面是算法的基础。然后计算点到平面的距离。
下面点云为 RANSAC 算法的结果，紫色区域代表车辆（RANSAC 在这里应该只用来区分地面了）：
RANSAC 是一个非常强大和简单的点云分割算法。它试图找到属于同一形状的点云和不属于同一形状的点云，然后将其分开。
4. 障碍聚类
4.1 点云聚类
RANSAC 的输出是障碍点云和地面。由此，可以为每个障碍定义独立的簇。它是如何工作的？
聚类是一系列机器学习算法，包括：k-means（最流行）、DBScan、HDBScan 等。这里可以简单地使用欧几里德聚类，计算点之间的欧几里德距离。
4.1.1 计算 KD-Tree
在进行点云聚类问题时，由于一个激光雷达传感器可以输出几万个点云，这将意味有上万次的欧几里德距离计算。为了避免计算每个点的距离，这里使用 KD-Tree 进行加速。
KD-Tree 是一种搜索算法，它将根据点在树中的XY位置对点进行排序，一般的想法-如果一个点不在定义的距离阈值内，那么x或y更大的点肯定不会在这个距离内。这样，我们就不必计算每一个点云。
4.1.2 欧式聚类
过程如下：
- 选取两个点，一个目标点和一个当前点；
- 如果目标和当前点之间的距离在距离公差范围内，请将当前点添加到簇中。
- 如果没有，选择另一个当前点并重复。
点云欧式聚类算法就是将一组点云按其距离进行分割。聚类算法以距离阈值、最小聚类数目和最大聚类数目作为输入。通过这种方式，可以过滤“幽灵障碍物”（一个单点云在空间中是没有理由存在的），并定义一个封闭的障碍物距离。如下图这里用不同颜色来代表聚类后的障碍物点云簇。
4.2 最邻近(NN)问题
- K-NN 在空间 M M M 中给定点集 S S S，一个查询点 q ∈ M q\in M q∈M，在 S S S 中查找 k k k 个最近点。
- Fixed Radius-NN 在空间 M M M 中给定点集 S S S，一个查询点 q ∈ M q\in M q∈M，在 S S S 中查找所有符合 ∣ ∣ s − q ∣ ∣ < r ||s-q||<r ∣∣s−q∣∣<r 的点。
4.2.1 为什么 NN 问题很重要
- 它几乎无处不在 - 表面法向量估计- 噪声滤波- 采样- 聚类- 深度学习- 特征检测 / 描述
- 为什么不简单的直接调用开源库（flann, PCL, ect.） - 它们不够高效：它们是通常使用的库，没有对 2D/3D 做优化；大多数开源的八叉树实现是低效的，而八叉树在 3D 中是最有效率的- 很少有 NN 库基于 GPU 的
4.2.2 为什么点云的 NN 很困难
- 不规则：点云可以分布在任何地方
- 维度灾难：点云可以是三维的，与二维相比的数据量是指数上升的。也可以建立一个三维网格，将点云转化成图像一样的东西，但是网格大部分区域是空白的，而且网格大小的选取也是一个问题。因此使用网格并不高效。
4.2.1 为什么最邻近在点云中如此困难
图像：
一个邻居简单的表示为
x
+
Δ
x
,
y
+
Δ
y
x+\Delta x,y+\Delta y
x+Δx,y+Δy.
点云：
- 不规则的：可以分布在图像中任何一个地方；
- 维数灾难：网格大部分是空白的，原理上就很低效。
4.3 BST(Binary Search Tree), kd-tree, octree 核心思想
- 空间分割： 1. 将空间划分成不同面积； 2. 只寻找一部分区域，而不是所有的数据点。
- 停止标准： 1. 如何跳过一些区域：每个区域都会有一个最差距离； 2. 如何停止 k-NN/radius-NN 查找: 如果知道可能的结果都在某个区间里面，那么查找完就结束了；
4.4 二叉树
BST 是一个基于节点的树结构：
- 左边的 key 都要比中间 root 小，右边的大。
一个节点包含：
- Key；
- Left child;
- Right child;
- … …
4.4.1 BST 构建/插入
比较小放左边，比较大放右边。如果左右边被占据了，就跟左右边被占据的继续对比。
给定一个一维点集
{
x
1
,
x
2
,
.
.
.
,
x
n
}
,
x
i
∈
R
\{x_1, x_2, ...,x_n\},x_i\in\R
{x1,x2,...,xn},xi∈R，如一个数组：
[
100
,
20
,
500
,
10
,
30
,
40
]
[100,20,500,10,30,40]
[100,20,500,10,30,40]
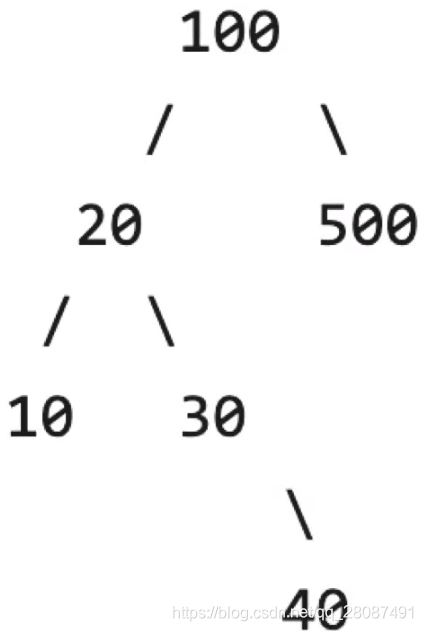
4.4.1.1 BST 插入复杂度
最坏的情况是
O
(
h
)
O(h)
O(h)，在这里
h
h
h 为在 BST 中点的个数。如将数组 [9,8,7,6,5,4,3] 按顺序插入进一个空的 BST 中：
这是一个合法的二叉树但它一无是处。平衡二叉树是另一个话题了。最佳情况：
h
=
l
o
g
2
n
h=log_2n
h=log2n。
4.4.2 BST 查找
给定一个 BST 和一个待查找 key，决定哪一个 node 等于这个 key，如果没有，则返回 NULL。
4.4.3 1NN 查找最邻近
比如说在下图中查找点 11：
1. 根节点为 8，这时最坏距离为 11-8=3。11比8大，这时知道要查找的范围在（8,14）之间，右边子树在范围（8，+inf），往右边看；
2. 到节点 10，这时最坏距离为 11-10=1，这时知道要查找的范围在（10,12）之间，因此不用往右边看，这时右边是比 10 大的，往右边看；
3. 到节点 14，最坏距离依旧为 1。这时要不要找 14 左边子节点？是需要的，左边的子节点比 14 小，要找的仍是（10,12）之间；
4. 找到 13，发现没什么变化，这时子节点已经遍历完了，退回 14；
5. 同理退回 10；
6. 同理退回 8
这样子就省去了五个比较的操作。
4.4.4 kNN 查找最邻近（N 个最邻近）
- 做法上几乎与 1NN 完全相同，区别在于计算最坏距离。
原始的二叉树比较难用于高维的最邻近搜索，因为二叉树搜索方法依赖一个特性：左边小，右边大。对于一维数据来说，可以比较距离有多少，但如果这是个高维数据就不行了。
4.5 Kd-tree
Kd-tree 就是在每个维度上做一个二叉树。但是它有一个更为复杂的地方是，每一个节点包含很多内容。
4.5.1 Kd-tree的构建
- 如果只有一个点，或者 点数<leaf_size，搭建一个 leaf；
- 否则的话，选取一个垂直于选定划分轴的超平面（三维就是一个平面），将点分为两半；
- 迭代重复前两步骤。
4.5.2 Kd-tree的两种方式
左边的情况是找到一个超平面，将超平面放在数据点上；
右边的超平面不属于任何点。
下面是树的两种切法，这里的波浪线是个二位数据。第一步在中间切一刀，第二步：
- 1.之前竖着切了一刀，后面切就是水平的了，轮流切；
- 2.有另外一种切法，叫做自适应。因为我们切这一刀是为了让点在每个维度的分布上更加平均。图中的数据即使中间切了一刀，其他数据也更像是水平分布的，因此再在水平来两刀。
这两种方式结果上是一样的，只是第二种可能速度会更快一点，使树更加平衡。
5. 边界框
最终的目标是围绕每个点云簇创建一个三维边界框。因为我们没有对点云簇进行任何分类，所以我们必须将边界框与点云相匹配。主成分分析(PCA)是一种有助于拟合边界框的算法。
5.1 PCA
PCA 用来找到点云的主方向。物理意义：将数据点都投影到一个非常有特征性的方向上 ，每一个点在这个方向上的投影就是主成分。如下图所示，在三维情况下，这个椭圆的主成分就是它的三个轴。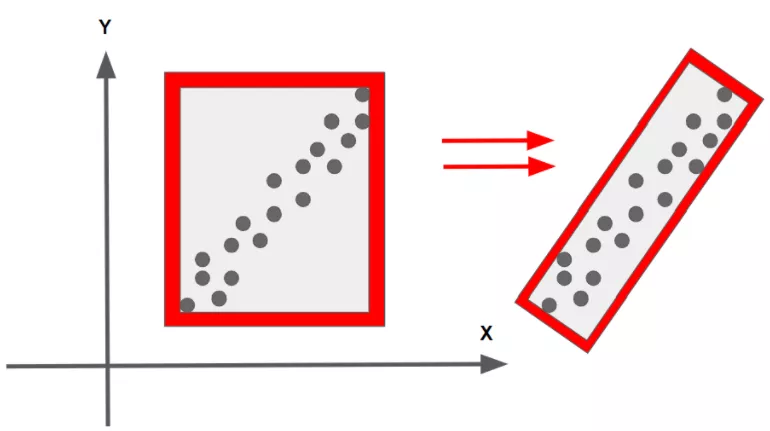
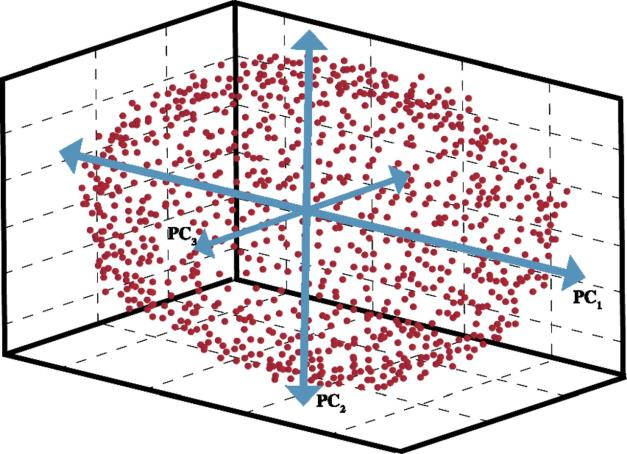
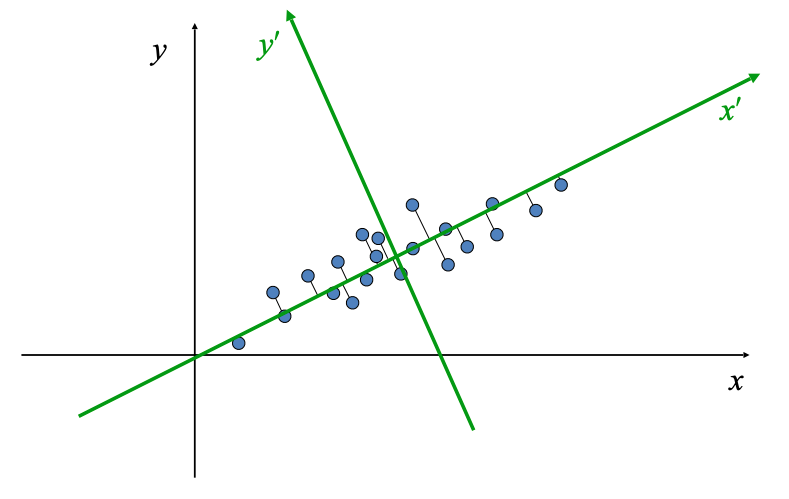
5.1.1 PCA 应用
- 降维；
- 平面法线估计；
- Canonical orientation(典型方向?)；
- 关键点检测；
- 特征描述。
5.1.2 Singular Value Decomposition (SVD)
比如有一个矩阵
M
M
M，它可以被分解为
U
U
U,
Σ
\Sigma
Σ,
V
∗
V^*
V∗，其中
U
U
U 和
V
∗
V^*
V∗ 都是正交矩阵；
Σ
\Sigma
Σ 是一个对角阵，它在对角线上组成了
M
M
M 的特征值。
假设我们把
M
M
M 乘上一个向量：
- 应用 V ∗ V^* V∗，其实就是在高维空间对向量做一个旋转，所以这个圆被旋转了一下；
Σ \Sigma Σ 对旋转后的向量在每一个维度上做一个缩放，所以这个圆就变成了一个椭圆；- 再应用 U U U， U U U 也是高维上的一个旋转矩阵，所以又把椭圆旋转了一下。 所以让 M 乘上一个向量，就是把一个圆变成了一个椭圆。
5.1.3 PCA 理论
- 输入： x i ∈ R n , i = 1 , 2 , . . . , m x_i\in \mathbb{R}^n,i=1,2,...,m xi∈Rn,i=1,2,...,m，其中 x i x_i xi 为高维空间中的向量。
- 输出：主要的向量 z 1 , z 2 , . . . , z k ∈ R m , k ≤ n z_1,z_2,...,z_k\in \mathbb{R}^m,k\leq n z1,z2,...,zk∈Rm,k≤n，其中 z 1 z_1 z1 为最主要的向量，描述了 x i x_i xi 这一群点里面最有代表性的高维方向。
1. 什么叫做最主要的成分？
如果把这堆高维点投影到某一个方向上，这些投影后的点的方差是最大的。也就是说，这些点在这个方向上分布的非常散。
2. 如何得到第二主要的成分？
把这一组输入
x i x_i xi 里面的、属于 z 1 z_1 z1 的成分都去掉，然后再找剩下的东西里面的最主要成分。
3. 如何得到第三主要的成分？
同上，去掉第一、二主要的成分。
总结：
输入：
x
i
∈
R
n
,
i
=
1
,
2
,
.
.
.
,
m
x_i\in \mathbb{R}^n,i=1,2,...,m
xi∈Rn,i=1,2,...,m，怎么做 PCA？
- 标准化数据，即减去数据的中心： X ~ = [ x ~ 1 , ⋯ , x ~ m ] , x ~ i = x i − x ˉ , i = 1 , ⋯ , m x ˉ = 1 m ∑ i = 1 m x i \tilde{X}=\left[\tilde{x}{1}, \cdots, \tilde{x}{m}\right], \tilde{x}{i}=x{i}-\bar{x}, i=1, \cdots, m \quad \bar{x}=\frac{1}{m} \sum_{i=1}^{m} x_{i} X
=[x1,⋯,xm],xi=xi−xˉ,i=1,⋯,mxˉ=m1i=1∑mxi - 计算 SVD： H = X ~ X ~ T = U r Σ 2 U r T H=\tilde{X} \tilde{X}^{T}=U_{r} \Sigma^{2} U_{r}^{T} H=X
XT=UrΣ2UrT - 主向量为 U r U_r Ur 的列，第一个主向量就是 U r U_r Ur 的第一列，第二个就是第二列，以此类推。
5.1.4 PCA 应用一：降维
将高维数据点投影到低维去，尽可能保留他们的特征。
给定
x
i
∈
R
n
,
i
=
1
,
2
,
.
.
.
,
m
x_i\in \mathbb{R}^n,i=1,2,...,m
xi∈Rn,i=1,2,...,m，使用 PCA 找到它的
l
l
l 个主向量
z
1
,
z
2
,
.
.
.
,
z
l
,
z
j
∈
R
n
{z_1,z_2,...,z_l},z_j\in \mathbb{R}^n
z1,z2,...,zl,zj∈Rn:
- 将 x i x_i xi 从 n n n 维压缩（映射）到 l l l 维 l < < n l<<n l<<n。Encoder：计算每个 x x x 在每一个方向上的投影： [ a i 1 ⋮ a i l ] = [ z 1 T ⋮ z l T ] x i \left[\begin{array}{c} a_{i 1} \ \vdots \ a_{i l} \end{array}\right]=\left[\begin{array}{c} z_{1}^{T} \ \vdots \ z_{l}^{T} \end{array}\right] x_{i} ⎣⎢⎡ai1⋮ail⎦⎥⎤=⎣⎢⎡z1T⋮zlT⎦⎥⎤xi
- 怎样再从 l l l 维重新回到 n n n 维：Decoder： x ^ i = ∑ j = 1 l a j z j = [ z 1 , ⋯ , z l ] [ a i 1 ⋮ a i l ] \hat{x}{i}=\sum{j=1}^{l} a_{j} z_{j}=\left[z_{1}, \cdots, z_{l}\right]\left[\begin{array}{c} a_{i 1} \ \vdots \ a_{i l} \end{array}\right] x^i=j=1∑lajzj=[z1,⋯,zl]⎣⎢⎡ai1⋮ail⎦⎥⎤
经过降维再升维肯定有数据上的损失，只是损失的比较少 。
从图中可以看到，在主向量上投影下来，仍可以看到有两坨点；而在第二个主向量上就只有一个波峰了。也可以再次说明主向量上保留了更多的信息。
5.1.5 Kernel PCA
在 5.1.4 中提到的都是普通的 PCA，普通 PCA 是线性的，因为矩阵乘法其实也就是一个线性操作（矩阵乘上一个向量其实是对一个矩阵的线性组合）。在遇到的数据不是一个线性的情况下，该怎么办？如左图的同心圆，做线性PCA很难区分开来，如右图所示，会得到两条线，没给出特别有意义的信息，比如将他们区分开。这时可以考虑在更高维度下进行操作。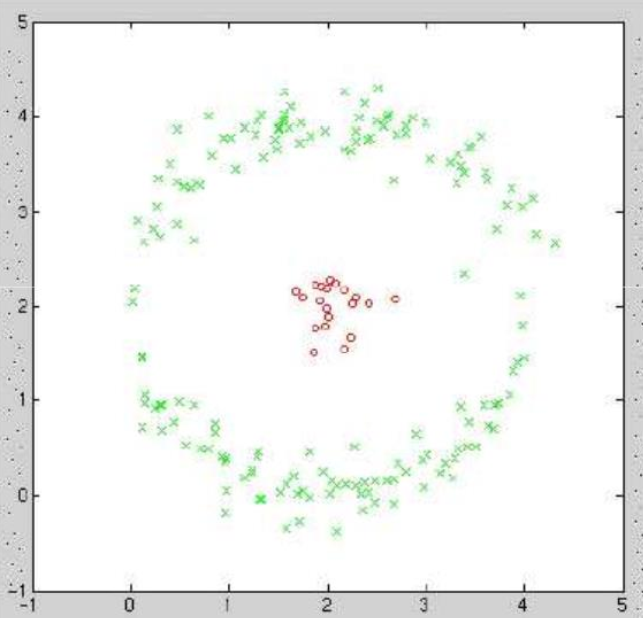
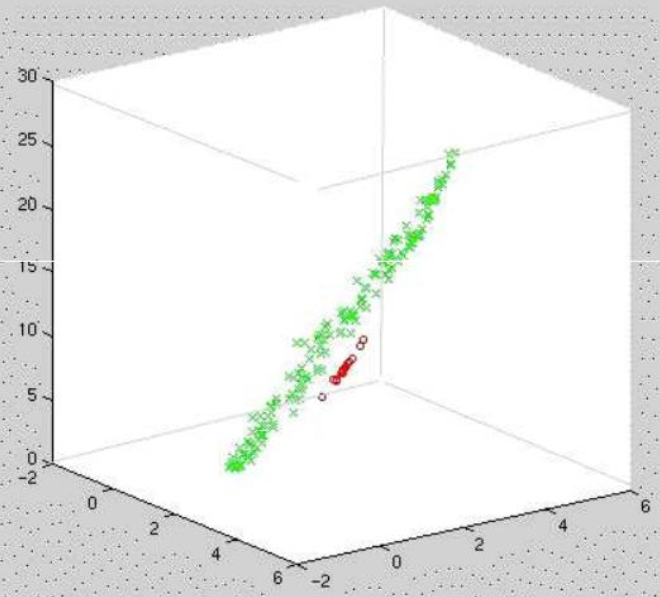
- 原始数据： x i = [ x i 1 , x i 2 ] ∈ R 2 x_i=[x_{i1}, x_{i2}] \in \mathbb{R}^2 xi=[xi1,xi2]∈R2
- 提升数据： ϕ ( x i ) = [ x i 1 , x i 2 , x i 1 2 + x i 2 2 ] ∈ R 3 \phi(x_i)=[x_{i1}, x_{i2},x_{i1}^2+x_{i2}^2] \in \mathbb{R}^3 ϕ(xi)=[xi1,xi2,xi12+xi22]∈R3，这里第三个维度选的平方和，就是极坐标的意思。 由上面右图可以看出，可以找到一个平面将它们区分开。这时我们只需要做一个普通的线性 PCA，就可以将它们区分开了。只不过这个时候是三维空间，不是二维空间。
刚刚所做的
[
x
i
1
,
x
i
2
,
x
i
1
2
+
x
i
2
2
]
[x_{i1}, x_{i2},x_{i1}^2+x_{i2}^2]
[xi1,xi2,xi12+xi22] 操作就是 kernel PCA。
Kernel PCA 步骤：
- 输入数据 x i ∈ R n 0 x_i\in \mathbb{R}^{n_0} xi∈Rn0，非线性映射 ϕ : R n 0 → R n 1 \phi: \mathbb{R}^{n_0}\rightarrow \mathbb{R}^{n_1} ϕ:Rn0→Rn1
- 与标准线性 PCA 在升维空间 R n 1 \mathbb{R}^{n_1} Rn1 上一样： 2.1 假设 ϕ ( x i ) \phi(x_i) ϕ(xi) 均值为零： 1 N ∑ i = 1 N ϕ ( x i ) = 0 \frac{1}{N} \sum_{i=1}^{N} \phi\left(x_{i}\right) =0 N1∑i=1Nϕ(xi)=0 2.2 计算协方差矩阵 H ~ = 1 N ∑ i = 1 N ϕ ( x i ) ϕ T ( x i ) \tilde{H}=\frac{1}{N} \sum_{i=1}^{N} \phi\left(x_{i}\right) \phi^{T}\left(x_{i}\right) H
=N1∑i=1Nϕ(xi)ϕT(xi)，加个波浪线因为是在高维空间上操作的，与原来的 H H H 区分开 2.3 解特征值/特征向量 H ~ z ~ = λ ~ z ~ \tilde{H}\tilde{z}=\tilde{\lambda}\tilde{z} Hz=λz~
现仍存在的问题：
- 如何定义映射 ϕ \phi ϕ?
- 升维后的维度可能会非常高，有没有办法来避免高维运算、节省运算资源？
特征向量可以表达为数据点的线性组合
z
~
=
∑
j
=
1
N
α
j
ϕ
(
x
j
)
\tilde{z}=\sum_{j=1}^{N} \alpha_{j} \phi\left(x_{j}\right)
z~=∑j=1Nαjϕ(xj)-----找到了系数
α
j
\alpha_j
αj 即找到了特征向量
z
~
\tilde{z}
z~。
证明：
H
~
z
~
=
λ
~
z
~
1
N
∑
i
=
1
N
ϕ
(
x
i
)
ϕ
T
(
x
i
)
z
~
=
λ
~
z
~
\tilde{H} \tilde{z}=\tilde{\lambda} \tilde{z} \\\frac{1}{N} \sum_{i=1}^{N} \phi\left(x_{i}\right) \phi^{T}\left(x_{i}\right) \tilde{z}=\tilde{\lambda} \tilde{z}
H~z~=λ~z~N1i=1∑Nϕ(xi)ϕT(xi)z~=λ~z~其中
ϕ
T
(
x
i
)
z
~
\phi^{T}\left(x_{i}\right) \tilde{z}
ϕT(xi)z~ 是一个标量，所以最后的特征向量
z
~
\tilde{z}
z~ 就是
ϕ
(
x
i
)
\phi(x_i)
ϕ(xi) 的线性组合。
常用核函数的选择：
- Linear k ( x i , x j ) = x i T x j k\left(x_{i}, x_{j}\right)=x_{i}^{T} x_{j} k(xi,xj)=xiTxj
- Polynomial k ( x i , x j ) = ( 1 + x i T x j ) p k\left(x_{i}, x_{j}\right)=\left(1+x_{i}^{T} x_{j}\right)^{p} k(xi,xj)=(1+xiTxj)p
- Gaussian k ( x i , x j ) = e − β ∥ x i − x j ∥ 2 k\left(x_{i}, x_{j}\right)=e^{-\beta\left|x_{i}-x_{j}\right|_{2}} k(xi,xj)=e−β∥xi−xj∥2
- Laplacian k ( x i , x j ) = e − β ∥ x i − x j ∥ 1 k\left(x_{i}, x_{j}\right)=e^{-\beta\left|x_{i}-x_{j}\right|_{1}} k(xi,xj)=e−β∥xi−xj∥1
通常来说只能通过实验来判断哪个的效果好，除非对数据非常了解，知道该使用什么样子的核函数。
**真
⋅
\cdot
⋅步骤：**
- 选择一个核函数 k ( x i , x j ) k(x_i,x_j) k(xi,xj)，组合成一个 Gram matrix K ( i , j ) = k ( x i , x j ) K(i,j)=k(x_i,x_j) K(i,j)=k(xi,xj)
- 标准化 K K K，使得高维空间的平均值为0，其中 K ~ \widetilde{K} K 为经过处理的核函数矩阵； I 1 N \mathbb{I}{\frac{1}{N}} IN1 是数值全为 1 N \frac{1}{N} N1 的常数矩阵，即 I 1 N ( i , j ) = 1 N , ∀ i , j \mathbb{I}{\frac{1}{N}}(i,j)=\frac{1}{N},\forall i,j IN1(i,j)=N1,∀i,j： K ~ = K − 2 I 1 N K + I 1 N K I 1 N \widetilde{K}=K-2 \mathbb{I}_{\frac{1}{N}} K+\mathbb{\mathbb { I } _{\frac{1}{N}}} K \mathbb{\mathbb { I } _{\frac{1}{N}}} K=K−2IN1K+IN1KIN1
- 解 K ~ \tilde{K} K~ 的特征值/特征向量： K ~ α r = λ r α r \widetilde{K} \alpha_{r}=\lambda_{r} \alpha_{r} Kαr=λrαr
- 标准化 α r \alpha_r αr 使得它的模，即 α r T α r = 1 λ r \alpha_{r}^{T} \alpha_{r}=\frac{1}{\lambda_{r}} αrTαr=λr1
- 将任何一个数据点 x ∈ R n x\in \mathbb{R}^{n} x∈Rn，将它们投影到 r t h r^{th} rth 主向量 y r ∈ R y_r\in \mathbb{R} yr∈R上： y r = ϕ T ( x ) z ~ r = ∑ j = 1 N α r j k ( x , x j ) y_{r}=\phi^{T}(x) \tilde{z}{r}=\sum{j=1}^{N} \alpha_{r j} k\left(x, x_{j}\right) yr=ϕT(x)z~r=j=1∑Nαrjk(x,xj)
例子：
如下图所示，输入数据在线性 PCA 下不可分：
当 kernel PCA 使用二次多项式核函数
k
(
x
i
,
x
j
)
=
(
1
+
x
i
T
x
j
)
2
k\left(x_{i}, x_{j}\right)=\left(1+x_{i}^{T} x_{j}\right)^{2}
k(xi,xj)=(1+xiTxj)2 时，如左图所示，点通过第一映射
y
0
y_0
y0 就很明显的区分开了：
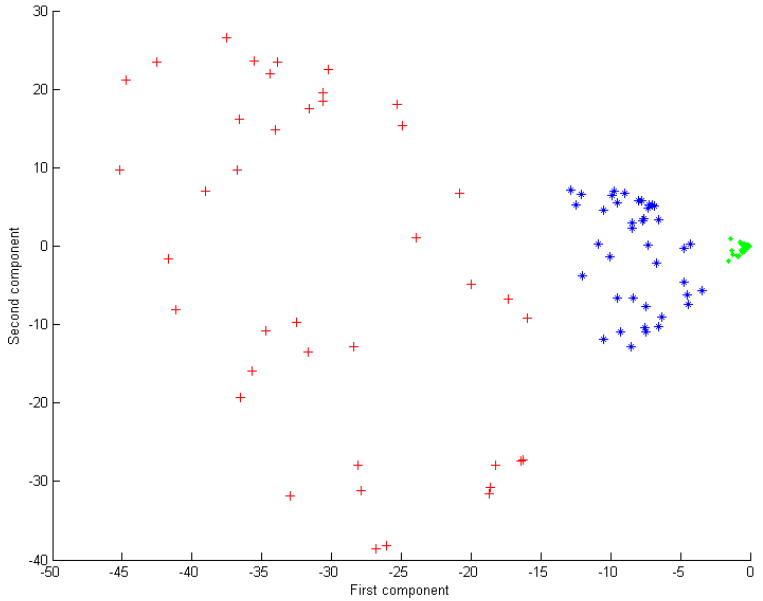
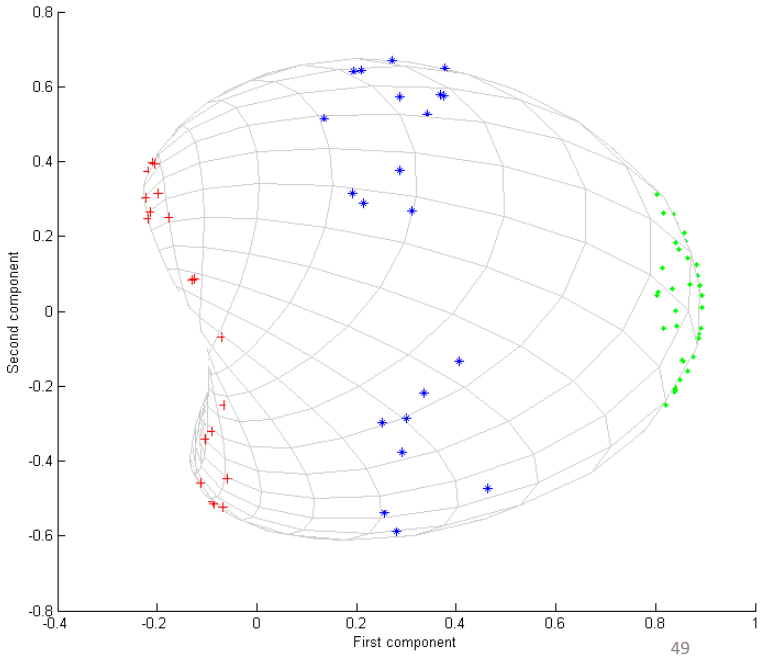
也可以使用高斯核函数
k
(
x
i
,
x
j
)
=
e
−
β
∥
x
i
−
x
j
∥
2
k\left(x_{i}, x_{j}\right)=e^{-\beta\left\|x_{i}-x_{j}\right\|_{2}}
k(xi,xj)=e−β∥xi−xj∥2，如上右图所示，区分的也很好。
5.1.5 PCA 应用
- 计算3D 点云的平面法向量 1.1 选取一个点 P P P； 1.2 找出这个点的邻域； 1.3 对邻域里的点做 PCA； 1.4 在邻域里选取的法向量是最不显著的向量； 1.5 曲率->特征值的比例 λ 3 / ( λ 1 + λ 2 + λ 3 ) \lambda_3/(\lambda_1+\lambda_2+\lambda_3) λ3/(λ1+λ2+λ3)。
/*************************** 额外的 *********************************/
6. 滤波
- 噪声去除 1.1 离群值清除(Raduius Outlier Removal) 1.2 统计离群值清除(Statistical Outlier Removal)
- 降采样：保存特征的同时，降低运算量 2.1 体素栅格降采样(Voxel Grid Downsampling) 2.2 最远点采样(Farthest Point Sampling) 2.3 法向量空间采样(Normal Space Sampling)
- 上采样/平滑 3.1 双边滤波(Bilateral Filter)
6.1 Noise removal
6.1.1 Radius Outlier
- 对于每个点，找到它在半径为 r r r 的邻居；
- 如果邻居的个数 k < k ∗ k<k^* k<k∗，则删除这个点。
6.1.2 升级版：Statistical Outlier Removal
- 对于每个点，找到它在半径为 r r r 的邻居；
- 计算每一个邻居距离这个点有多远 d i j , i = [ 1 , . . . , m ] , j = [ 1 , . . . , k ] d_{ij},i=[1,...,m],j=[1,...,k] dij,i=[1,...,m],j=[1,...,k]， i i i 为这个点， j j j 为邻居;
- 使用高斯分布对距离建模 d ∼ N ( μ , σ ) d\sim N(\mu,\sigma) d∼N(μ,σ)-----这里是对所有的点得到的一个总的建模结果，而不是对单个点 μ = 1 n k ∑ i = 1 m ∑ j = 1 k d i j , σ = 1 n k ∑ i = 1 m ∑ j = 1 k ( d i j − μ ) 2 \mu=\frac{1}{n k} \sum_{i=1}^{m} \sum_{j=1}^{k} d_{i j}, \sigma=\sqrt{\frac{1}{n k} \sum_{i=1}^{m} \sum_{j=1}^{k}\left(d_{i j}-\mu\right)^{2}} μ=nk1i=1∑mj=1∑kdij,σ=nk1i=1∑mj=1∑k(dij−μ)2
- 对于每个点，重新计算一遍对于邻居的平均距离（半径依旧为 r r r）；
- 去除这个点，如果平均距离大于一些阈值，如，当在以下条件下去除点： ∑ j = 1 k d i j > μ + 3 σ or ∑ j = 1 k d i j < μ − 3 σ \sum_{j=1}^{k} d_{i j}>\mu+3 \sigma \text { or } \sum_{j=1}^{k} d_{i j}<\mu-3 \sigma j=1∑kdij>μ+3σ or j=1∑kdij<μ−3σ下图为 Statistical Outlier Removal 的处理结果，右边红色为处理前的平均距离，经过滤波后邻居就特别近了。
6.2 Downsampling
6.2.1 Voxel Grid Downsampling
- 构建一个包含点云的体素栅格；
- 在每个单元中选取一个点。
这里存在两个问题：
- 如何选取这个点？
- 如何将该算法变得有效率？
版权归原作者 泠山 所有， 如有侵权，请联系我们删除。