系统辨识工具箱
什么时候使用系统辨识,当系统传递函数不确定(在多大程度上不确定?)时,通过对输入输出数据采集,通过数学迭代找到控制对象的近似模型。在找到近似模型(传递函数)后,就可以使用线性化调参工具对系统控制参数进行整定,进行控制系统设计。
调用命令:systemIdentification
一般过程:
将数据数组从matlab工作区导入程序;
绘制数据;
数据归一化;
估计、验证、线性模型;
模型导出到工作区
1输入输出数据的导入和处理
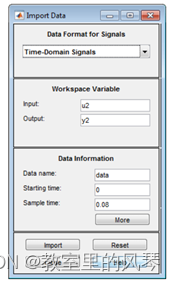
数据导入过程中,采样时间设置为真实系统的仿真时间
在more中的次级菜单可设置导入信号的名称和单位,如果是多路信号,这一步就很重要了。
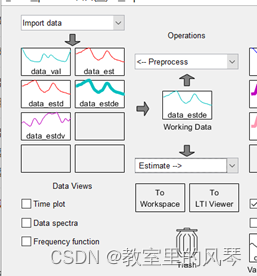
数据处理操作,可在process菜单中选择quick start选项,即可生成归一化后的输入和输出数据,并且划定了训练集和验证集。
2进行模型估计。同样可以使用quick start操作生成阶跃响应图imp、频率响应图spad、状态空间n4s3和多项式模型arxqs的输出,然后可以在模型输出modeloutput窗口窗口对比验证效果。
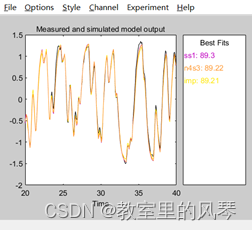
未生成spad模型的适应度值。
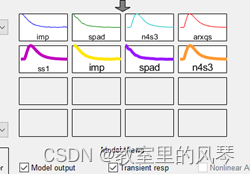
右键可查看模型相关信息。
除此之外,还可以使用基于其他算法的计算模型。
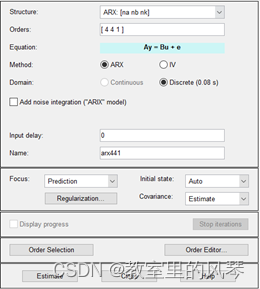 多项式方程。
多项式方程。
编辑Orders字段以尝试极点、零点和延迟的所有组合,其中每个值都从 1 到 10:
点击estimate,
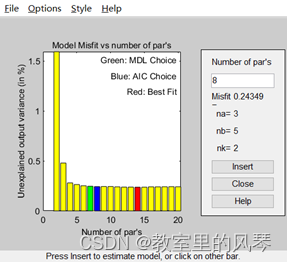 该窗口有3个突出显示部分:
该窗口有3个突出显示部分:
图中以绿色、蓝色和红色突出显示了三个矩形。每种颜色表示一种最佳拟合标准,如下所示:
红色——最佳拟合最小化验证数据输出和模型输出之间的差异的平方和。此矩形表示整体最佳拟合。
绿色 - 最佳拟合最小化了 Rissanen MDL 标准。
蓝色 — 最佳拟合最小化 Akaike AIC 标准。
基于MDL和AIC的标准补偿了因使用过多参数而导致的过拟合问题。
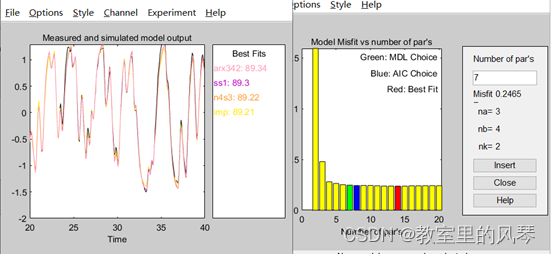
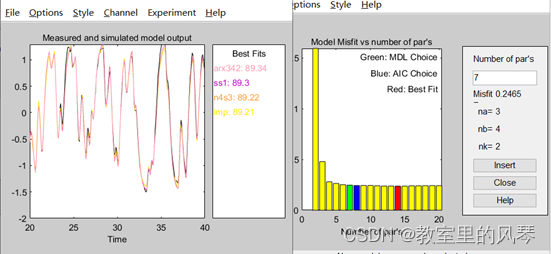
选择绿色图块对应的参数,insert,适应度为arx342所示。
对于estimate中的识别顺序其实是很关键的,因为实际中许多要辨识的系统特征(零极点分布状况)是未知的,所以不能一开始就选择传递函数模型进行辨识。
在使用利用多项式辨识过程中,得到了三种评估标准下的模型零极点个数,为后续其他数据模型辨识提供了基础。在上述ARX模型中,最终最佳拟合的模型分布为极点个数为3,零点为4,延迟为2。
下面就基于上述零极点分布情况对传递函数进行估计。
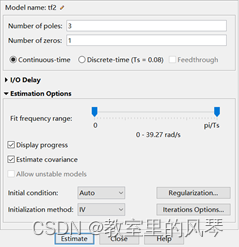
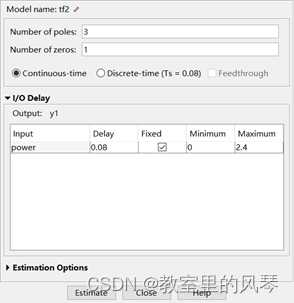
根据上上面估计后得到的零极点个数可以预设传递函数极点状况(3 4 2),不过零点个数保留系统默认值1,延迟环节换算公式为(样本延迟nk=2)转换为连续时间延迟为(nk-1)*Ts
拟合度如图,这比直接进行传递函数估计要来的准确。
下面使用状态空间模型估计,同样是基于多项式估计的基础,全体最佳拟合度极零点分布(3 4 2),估计时仅需给定阶数(极点个数)即可。
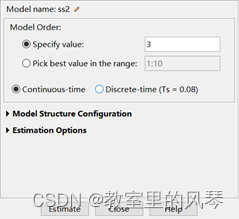
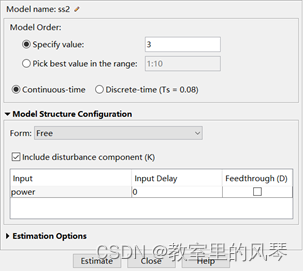
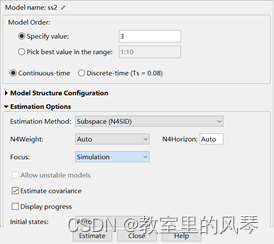
Focus设置为模拟输出。当然,这个选项也可以在拟合度窗口进行统一设置。
还可以使用ARMAX模型进行系统模拟,它比ARX更灵活,其结构中包含一个额外的多项式来模拟附加性扰动。
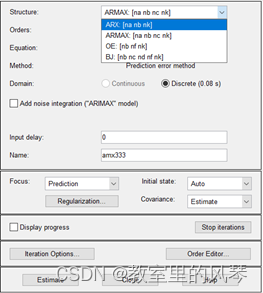
设置结构列表。
前述使用ARX估计最佳拟合极零点分布为3 4 2,可以从这些数目组合开始,最后再加上一列。
 从2 2 2 2开始。
从2 2 2 2开始。
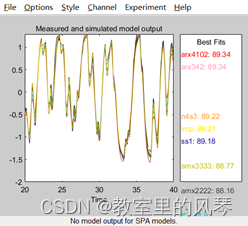 3 3 3 3
3 3 3 3
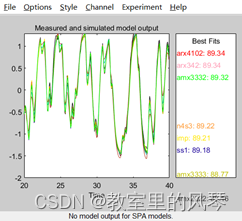 3 3 3 2
3 3 3 2
这已经十分接近ARX模型了。
辨识得到的模型可导入到工作区,进行下一步工作。选取适应度最佳的模型导出到工作区中。
 然后可以使用模型转换工具得到相应传递函数
然后可以使用模型转换工具得到相应传递函数

反向验证:将识别得到的传递函数添加到simulink中,输入数据为识别过程中的原始输入数据,比较实际输出和原输出数据。
首先制作输入数据,在simulink中的输入数据需要是实数、整型、浮点数,且第一列为时间数据,因此结合原数据采样时间为0.08s,可得制作数据时间间隔为0.08s,数据量为1000,因此时间为0-0.08*1000s
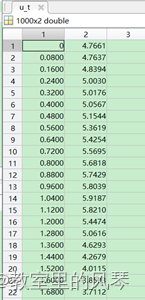
验证模型
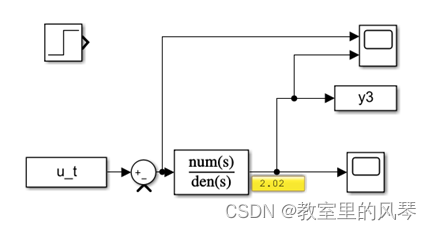
待验证传递函数:
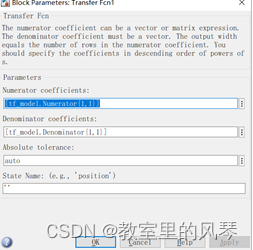
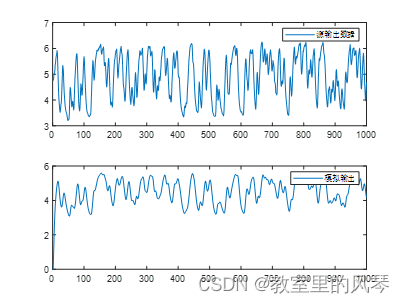 测试输出
测试输出
均方根误差:
版权归原作者 教室里的风琴 所有, 如有侵权,请联系我们删除。