【OpenCV 完整例程】63. 图像锐化——Laplacian 算子
欢迎关注 『OpenCV 完整例程 100 篇』 系列,持续更新中
欢迎关注 『Python小白的OpenCV学习课』 系列,持续更新中
3. 空间域锐化滤波(高通滤波)
图像模糊通过平滑(加权平均)来实现,类似于积分运算。图像锐化则通过微分运算(有限差分)实现,使用一阶微分或二阶微分都可以得到图像灰度的变化值。
图像锐化的目的是增强图像的灰度跳变部分,使模糊的图像变得清晰。图像锐化也称为高通滤波,通过和增强高频,衰减和抑制低频。图像锐化常用于电子印刷、医学成像和工业检测。
- 恒定灰度区域,一阶导数为零,二阶导数为零;
- 灰度台阶或斜坡起点区域,一阶导数非零,,二阶导数非零;
- 灰度斜坡区域,一阶导数非零,二阶导数为零。
图像梯度提取方法简单直接,能够有效的描述图像的原始状态,因此发展出多种图像梯度算子:Roberts、Prewitt、Sobel、Laplacian、Scharr。
3.3 拉普拉斯卷积核(Laplacian)
各向同性卷积核的响应与方向无关。最简单的各向同性导数算子(卷积核)是拉普拉斯算子(Laplace):
∇
2
f
=
∂
2
f
∂
x
2
+
∂
2
f
∂
y
2
∂
2
f
∂
x
2
=
f
(
x
+
1
,
y
)
−
2
f
(
x
,
y
)
+
f
(
x
−
1
,
y
)
∂
2
f
∂
y
2
=
f
(
x
,
y
+
1
)
−
2
f
(
x
,
y
)
+
f
(
x
,
y
−
1
)
∇
2
f
(
x
,
y
)
=
f
(
x
+
1
,
y
)
+
f
(
x
−
1
,
y
)
+
f
(
x
,
y
+
1
)
+
f
(
x
,
y
−
1
)
−
4
f
(
x
,
y
)
\begin{aligned} \nabla ^2 f &= \dfrac{\partial ^2 f}{\partial x ^2} + \dfrac{\partial ^2 f}{\partial y ^2} \\ \dfrac{\partial ^2 f}{\partial x ^2} &= f(x+1,y) - 2f(x,y) + f(x-1,y) \\ \dfrac{\partial ^2 f}{\partial y ^2} &= f(x,y+1) - 2f(x,y) + f(x,y-1) \\ \nabla ^2 f(x,y) &= f(x+1,y) + f(x-1,y) + f(x,y+1) + f(x,y-1) - 4f(x,y) \end{aligned}
∇2f∂x2∂2f∂y2∂2f∇2f(x,y)=∂x2∂2f+∂y2∂2f=f(x+1,y)−2f(x,y)+f(x−1,y)=f(x,y+1)−2f(x,y)+f(x,y−1)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
由此可以得到拉普拉斯核 K1。类似地,考虑对角项后可以得到拉普拉斯核 K2。
K
1
=
[
0
1
0
1
−
4
1
0
1
0
]
,
K
2
=
[
1
1
1
1
−
8
1
1
1
1
]
,
K
3
=
[
0
−
1
0
−
1
4
−
1
0
−
1
0
]
,
K
4
=
[
−
1
−
1
−
1
−
1
8
−
1
−
1
−
1
−
1
]
K1= \begin{bmatrix} 0 & 1 &0\\ 1 & -4 &1\\ 0 & 1 &0\\ \end{bmatrix}, \ K2= \begin{bmatrix} 1 & 1 &1\\ 1 & -8 &1\\ 1 & 1 &1\\ \end{bmatrix}, \ K3= \begin{bmatrix} 0 & -1 &0\\ -1 & 4 &-1\\ 0 & -1 &0\\ \end{bmatrix}, \ K4= \begin{bmatrix} -1 & -1 &-1\\ -1 & 8 &-1\\ -1 & -1 &-1\\ \end{bmatrix}
K1=⎣⎡0101−41010⎦⎤, K2=⎣⎡1111−81111⎦⎤, K3=⎣⎡0−10−14−10−10⎦⎤, K4=⎣⎡−1−1−1−18−1−1−1−1⎦⎤
Laplace 是导数算子,会突出图像中的急剧灰度变化,抑制灰度缓慢变化区域,往往会产生暗色背景下的灰色边缘和不连续图像。将拉普拉斯图像与原图叠加,可以得到保留锐化效果的图像。
拉普拉斯卷积核很容易通过卷积操作 cv. filter_2d 实现,OpenCV 也提供了拉普拉斯算子 cv.Laplacian 来实现。
函数说明:
cv.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]]) → dst
参数说明:
- src:输入图像,可以是灰度图像,也可以是多通道的彩色图像
- ddepth:输出图片的数据深度:
- dst:输出图像,大小和类型与 src 相同
- ksize:计算二阶导数滤波器的孔径大小,必须为正奇数,可选项
- scale:缩放比例因子,可选项,默认值为 1
- delta:输出图像的偏移量,可选项,默认值为 0
- borderType:边界扩充的类型,注意不支持对侧填充(BORDER_WRAP)
例程 1.78:图像锐化:Laplacian 算子
# 1.78:图像锐化:拉普拉斯算子 (Laplacian)
img = cv2.imread("../images/Fig0338a.tif", flags=0)# NASA 月球影像图# 使用函数 filter2D 实现 Laplace 卷积算子
kernLaplace = np.array([[0,1,0],[1,-4,1],[0,1,0]])# Laplacian kernel
imgLaplace1 = cv2.filter2D(img,-1, kernLaplace, borderType=cv2.BORDER_REFLECT)# 使用 cv2.Laplacian 实现 Laplace 卷积算子
imgLaplace2 = cv2.Laplacian(img,-1, ksize=3)
imgRecovery = cv2.add(img, imgLaplace2)# 恢复原图像# 二值化边缘图再卷积
ret, binary = cv2.threshold(img,0,255, cv2.THRESH_BINARY | cv2.THRESH_TRIANGLE)
imgLaplace3 = cv2.Laplacian(binary, cv2.CV_64F)
imgLaplace3 = cv2.convertScaleAbs(imgLaplace3)
plt.figure(figsize=(9,6))
plt.subplot(131), plt.axis('off'), plt.title("Original")
plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.subplot(132), plt.axis('off'), plt.title("cv.Laplacian")
plt.imshow(imgLaplace2, cmap='gray', vmin=0, vmax=255)
plt.subplot(133), plt.axis('off'), plt.title("thresh-Laplacian")
plt.imshow(imgLaplace3, cmap='gray', vmin=0, vmax=255)
plt.tight_layout()
plt.show()
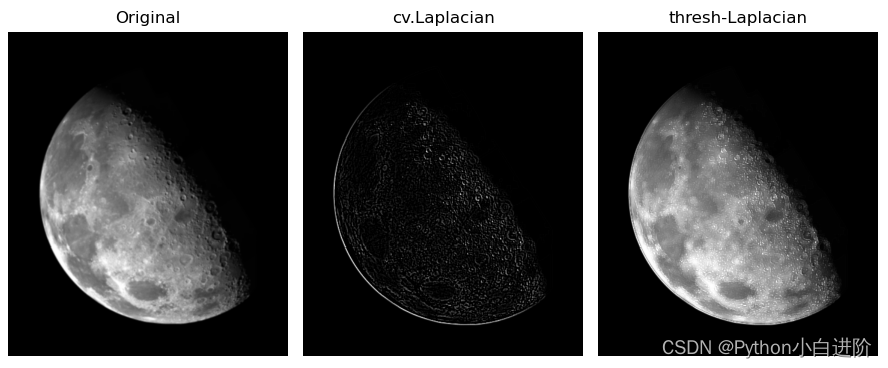
由于拉普拉斯卷积核很敏感,可以先进行阈值化处理,再进行拉普拉斯卷积。例程对比了直接进行拉普拉斯卷积,与阈值化处理后进行拉普拉斯卷积,结果如下图所示。
(本节完)
版权声明:
youcans@xupt 原创作品,转载必须标注原文链接
Copyright 2021 youcans, XUPT
Crated:2021-11-29
欢迎关注 『OpenCV 完整例程 100 篇』 系列,持续更新中
欢迎关注 『Python小白的OpenCV学习课』 系列,持续更新中【OpenCV 完整例程】01. 图像的读取(cv2.imread)
【OpenCV 完整例程】02. 图像的保存(cv2.imwrite)
【OpenCV 完整例程】03. 图像的显示(cv2.imshow)
【OpenCV 完整例程】04. 用 matplotlib 显示图像(plt.imshow)
【OpenCV 完整例程】05. 图像的属性(np.shape)
【OpenCV 完整例程】06. 像素的编辑(img.itemset)
【OpenCV 完整例程】07. 图像的创建(np.zeros)
【OpenCV 完整例程】08. 图像的复制(np.copy)
【OpenCV 完整例程】09. 图像的裁剪(cv2.selectROI)
【OpenCV 完整例程】10. 图像的拼接(np.hstack)
【OpenCV 完整例程】11. 图像通道的拆分(cv2.split)
【OpenCV 完整例程】12. 图像通道的合并(cv2.merge)
【OpenCV 完整例程】13. 图像的加法运算(cv2.add)
【OpenCV 完整例程】14. 图像与标量相加(cv2.add)
【OpenCV 完整例程】15. 图像的加权加法(cv2.addWeight)
【OpenCV 完整例程】16. 不同尺寸的图像加法
【OpenCV 完整例程】17. 两张图像的渐变切换
【OpenCV 完整例程】18. 图像的掩模加法
【OpenCV 完整例程】19. 图像的圆形遮罩
【OpenCV 完整例程】20. 图像的按位运算
【OpenCV 完整例程】21. 图像的叠加
【OpenCV 完整例程】22. 图像添加非中文文字
【OpenCV 完整例程】23. 图像添加中文文字
【OpenCV 完整例程】23. 图像添加中文文字
【OpenCV 完整例程】24. 图像的仿射变换
【OpenCV 完整例程】25. 图像的平移
【OpenCV 完整例程】26. 图像的旋转(以原点为中心)
【OpenCV 完整例程】27. 图像的旋转(以任意点为中心)
【OpenCV 完整例程】28. 图像的旋转(直角旋转)
【OpenCV 完整例程】29. 图像的翻转(cv2.flip)
【OpenCV 完整例程】30. 图像的缩放(cv2.resize)
【OpenCV 完整例程】31. 图像金字塔(cv2.pyrDown)
【OpenCV 完整例程】32. 图像的扭变(错切)
【OpenCV 完整例程】33. 图像的复合变换
【OpenCV 完整例程】34. 图像的投影变换
【OpenCV 完整例程】35. 图像的投影变换(边界填充)
【OpenCV 完整例程】36. 直角坐标与极坐标的转换
【OpenCV 完整例程】37. 图像的灰度化处理和二值化处理
【OpenCV 完整例程】38. 图像的反色变换(图像反转)
【OpenCV 完整例程】39. 图像灰度的线性变换
【OpenCV 完整例程】40. 图像分段线性灰度变换
【OpenCV 完整例程】41. 图像的灰度变换(灰度级分层)
【OpenCV 完整例程】42. 图像的灰度变换(比特平面分层)
【OpenCV 完整例程】43. 图像的灰度变换(对数变换)
【OpenCV 完整例程】44. 图像的灰度变换(伽马变换)
【OpenCV 完整例程】45. 图像的灰度直方图
【OpenCV 完整例程】46. 直方图均衡化
【OpenCV 完整例程】47. 图像增强—直方图匹配
【OpenCV 完整例程】48. 图像增强—彩色直方图匹配
【OpenCV 完整例程】49. 图像增强—局部直方图处理
【OpenCV 完整例程】50. 图像增强—直方图统计量图像增强
【OpenCV 完整例程】51. 图像增强—直方图反向追踪
【OpenCV 完整例程】52. 图像的相关与卷积运算
【OpenCV 完整例程】53. Scipy 实现图像二维卷积
【OpenCV 完整例程】54. OpenCV 实现图像二维卷积
【OpenCV 完整例程】55. 可分离卷积核
【OpenCV 完整例程】56. 低通盒式滤波器
【OpenCV 完整例程】57. 低通高斯滤波器
【OpenCV 完整例程】58. 非线性滤波—中值滤波
【OpenCV 完整例程】59. 非线性滤波—双边滤波
【OpenCV 完整例程】60. 非线性滤波—联合双边滤波
【OpenCV 完整例程】61. 导向滤波(Guided filter)
【OpenCV 完整例程】62. 图像锐化——钝化掩蔽
【OpenCV 完整例程】63. 图像锐化——Laplacian 算子
版权归原作者 Python小白进阶 所有, 如有侵权,请联系我们删除。