AUC到底代表什么呢,我们从另外一个角度解释AUC,我们先看看一个auc曲线
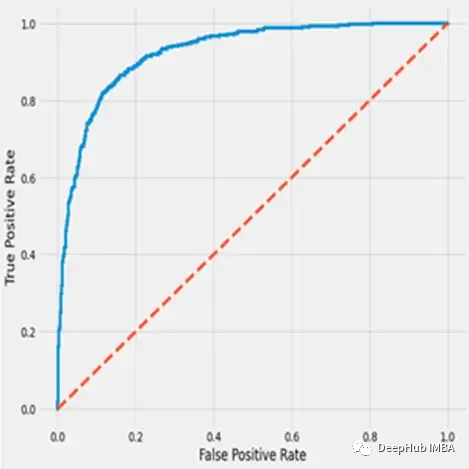
蓝色曲线下的面积(我的模型的AUC)比红线下的面积(理论随机模型的AUC)大得多,所以我的模型一定更好。
我的模型比随机模型好多少呢?理论随机模型只是对角线,这条对角线下的面积是0.5,我们的模型的AUC是0.75 那么这个0.75的AUC值究竟代表什么?
首先,我们要了解AUC是为一个可以给出概率分数的模型定义的。另外一点是,它是为二元分类任务定义的。但是也可以推广到多类分类问题。
我们要牢记以上这两点,这样才可以继续解释这个问题。
二元分类模型是什么样子的?
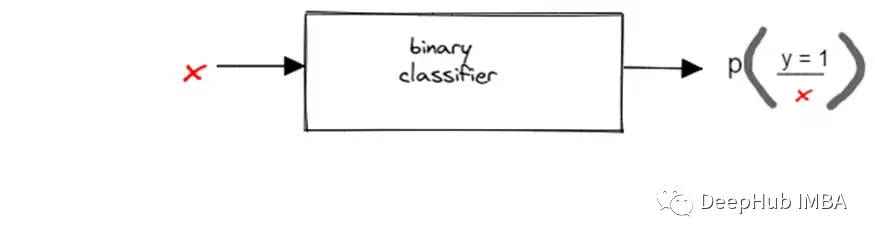
简单地说,给定一个数据点,比如x,它可以有许多特征,任何这样的数据点的类只能有两种可能性,要么是1,要么是0。而模型一般都会预测样本为1的概率(0-1之间的一个数值)。
也就是说,它不是直接断言类,而是预测一个类的概率。
我们得到了这个分数,可以把它看做是一个信心的衡量标准。如果你把钱押在两匹马上,x1和x2。你记录下它们的特征,然后通过分类器。第一个赢的概率是0.90第二个赢的概率是0.85。这两匹马都有相当不错的胜率,虽然这两个马的分类都是“win”(因为概率都超过了50%)。但是如果只有在一匹马上下注的钱,那么根据概率你会选择哪匹马呢?
在上面的讨论中,我们忽略了一个假设,这正是直观理解AUC的最基本方面。我如何判断这两匹马都属于这个类别呢?因为他们获胜的概率都很高(>0.5)。但是有多高呢?
为什么把这两匹马都归为类别获胜似乎是一件显而易见的事情?
因为在0到1的范围内(这是任何概率的范围),大于0.5或0.55的值应该被视为高值。但是,如果你真的要下注,而一匹马的概率是0.60,你会下注吗?我不这么认为!也就是说,你不关心0.5的门槛,你有一个更高的门槛因为你是在用真的钱在冒险,所以你可能会想拒绝0.6的那匹马是明智的。
如果把阈值提高到0.95上面提到的马x1和x2都会被拒绝。但是如果你的门槛是0.88,哪你会选择x2而拒绝x1。
也就是说,当涉及概率评分时分类结果将取决于0-1范围内阈值的选择。
这里我们首先假设有一个上帝模型,它会知道哪匹马会赢,所以它会输出获胜的概率分数,赢的马的概率分数为0.999,其他所有马的概率分数为0.0001。另外一个假设你是一个“傻瓜”,你会相信即使是一匹赢的概率等于0.1的马也会赢。
当我们的模型给出胜出的概率为0.25时,你肯定直接去柜台把钱押在那匹马身上(0.25>0.1)。但是如果你有上帝模型,它会直接输出0.0001,而你的阈值是0.1,因此你也不会在那匹马上下注,所以即使你是“傻瓜”,但上帝模型很好也可能给你正确的答案。也就是说无论你的阈值是多少,如果这个模型都很好,你就不会有损失。
因此,无论你的阈值是0.9还是0.95,上帝模型都会输出获胜马的概率分数为0.999,这将高于做出决定而设置的任何阈值。因此你将永远赢钱,永远不会赔钱。
对于上帝模型来说,True-Positive 率总是1,False-Positive率总是0。上帝模型的ROC曲线可以说是不存在的,因为在绘制它时,你会发现只有一个点,FP等于0,TP等于1。
TPR和FPR
让我们继续说说TPR和FPR。
TPR:在所有正例中,有多少被预测为正例的。
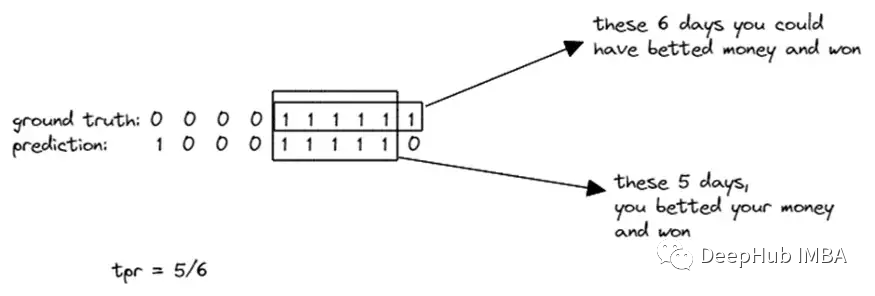
对于我们说的赛马来说,TPR是假设钱被押注的情况下的赢钱的概率。而FPR是在赌钱的情况下赔钱的比率。所以,我们希望TPR大于FPR。
FPR:在所有真正的负例中,有多少被预测为正例的
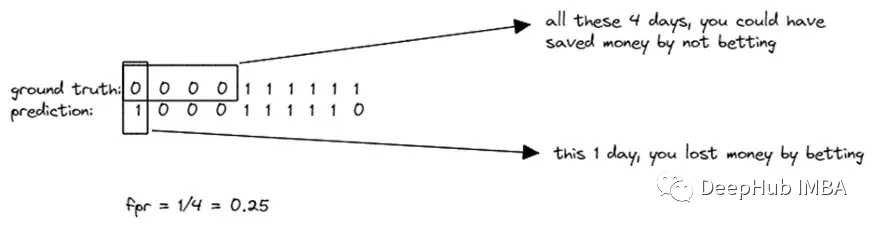
假设你的阈值太低,比如0.05。模型给出的任何概率值都可能高于阈值,因此每个实例都被预测为正例。在这种情况下,TPR和FPR都是1。类似的当阈值过高(如0.99)时,你的模型给出的任何概率分数都可能低于阈值,因此每个实例都被预测为负例。在这种情况下,TPR和FPR都等于0。

所以如果绘制这两个点,其中FPR =TPR =1和FPR =TPR =0,你会发现这两个点在对角线上。注意对角线的方程是FPR = TPR。他的含义是,如果模型对不同的截止点表现出这样的行为,我们可以保证不会因为损失而抵消你所赚的钱。
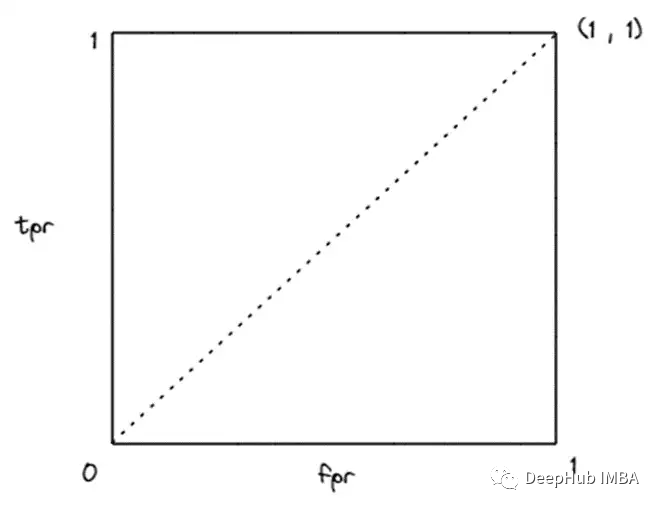
为了得到一个比随机模型更好、更接近上帝模型的模型,我们希望TPR在大多数截断点上大于FPR。
为什么呢?因为TPR是可能获胜的总数中的胜率,而 FPR 给出了下注的输钱率。对角线上方的区域是TPR大于FPR的区域。曲线越向上移动越好。
最后就是要量化这个概念,曲线下的面积是有意义的。曲线下的面积越大,曲线向上移动的幅度就越大。所以当看到TPR和FPR之间的曲线时,
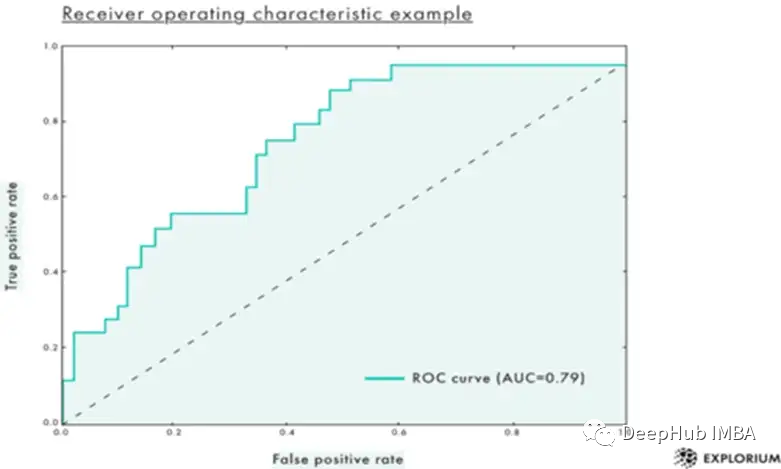
你会注意到曲线位于TPR > FPR的区域。通过AUC,你就知道它有多好。
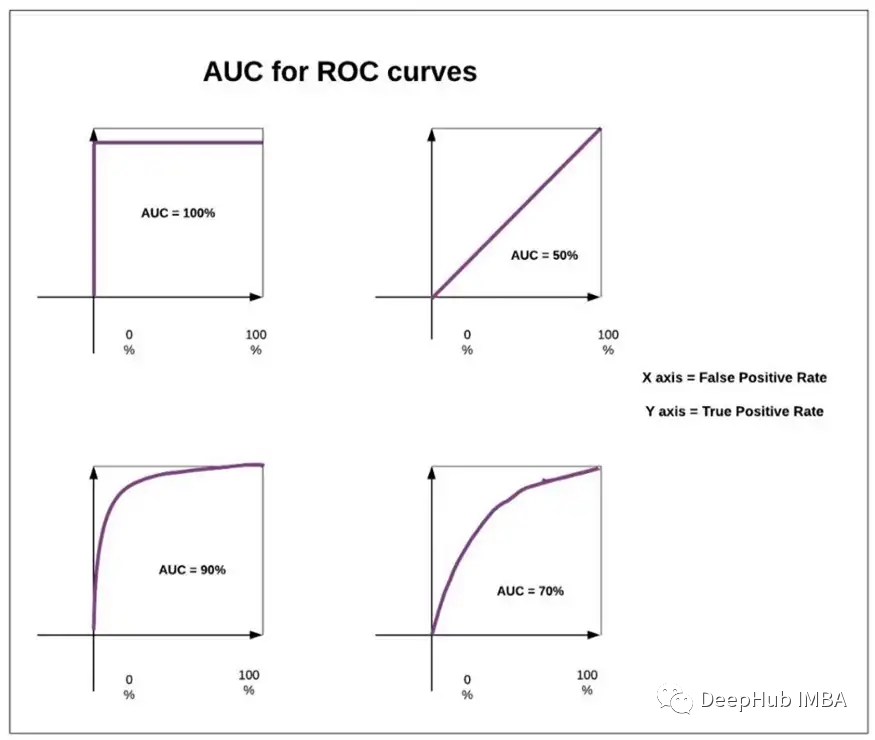
为什么要在TPR和FPR之间画一条曲线呢?
我们继续用赛马的例子中给出TPR和FPR的含义来解释这一点
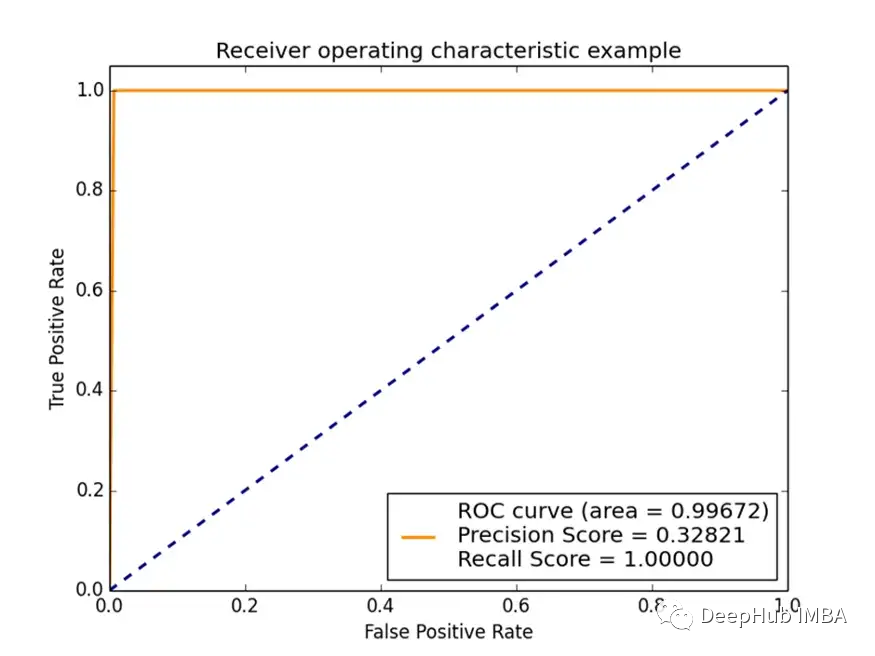
橙色的ROC曲线说明了什么?这条曲线通过绘制TPR与FPR在不同截点处的曲线而存在。这条曲线表明无论截点是多少,TPR总是等于1。
从这一点出发,截点用于检查模型的判别质量有多健壮。也就是说即使有不同的截点,模型给出的TPR值总会高于FPR值。具体高出多少呢?
AUC就给出的是给出“多高”的概念。因为我们感兴趣的是知道模型有多好?它能更好地区分两个类别(赢/输),我们赌赢钱越多,赌输钱越少的可能性就越大。
作者:Number Theory