摘要及声明
1:本文主要介绍决策树的实现方法及可视化方法;
2:本文主要为理念的讲解,模型也是笔者自建,文中假设与观点是基于笔者对模型及数据的一孔之见,若有不同见解欢迎随时留言交流;
3:笔者希望搭建出一套交易体系,原则是只做干货的分享。后续将更新更多内容,但工作学习之余的闲暇时间有限,更新速度慢还请谅解;
4:本文Python部分的数据通过Tushare金融大数据平台接口获取,R语言部分的数据是用笔者之前上学的作业;
5:本文模型实现基于python3.8及R 4.1.2;
由于笔者后面打算写的几篇主线文章会用到决策树,如果突然出一期主线内容又讲金融原理,又讲技术原理难免显得太过杂乱,于是决定先发一篇把技术实现解决,方便后续可以专注于金融原理上。本文同时通过Python和R语言实现决策树,最后进行了两种语言实现方式的比较,有特定语言需求的读者可以从目录直接跳转,本文主要内容如下:
1. 决策的本质是对数据集进行切分
·根据拟合因变量的类型,决策树可以分为两种:回归树(连续因变量)和分类树(离散因变量)。举个借钱给朋友的栗子,如果我们将收入作为借与不借的唯一标准,那么我们可以生成一颗分类树:
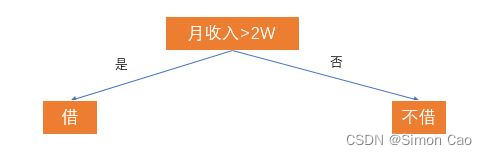
图一:树的要素:根,叶,决策判断条件
我们把月收入称作“根节点”,借与不借(树最下面一行的节点)两个子节点称为“叶”,“借”与“不借”则代表了从根到叶的决策路径。但现实生活中肯定不会那么简单,我们再加入一个失信次数的条件:
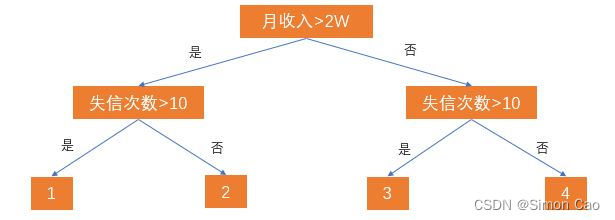
图二:简单的决策树
于是现在的树就分裂出四个叶节点。那么这四个节点分别代表:
1:月收入>2W,失信次数>10次,老赖;
2:月收入>2W,失信次数<=10次,还款能力高,信用高;
3:月收入<=2W,失信次数>10次,要钱没有要命一条;
4:月收入>=2W,失信次数<=10次,还款能力低,但比较诚信;
其实我们已经不知不觉将数据集拆分成了4份:

图三:决策树对数据集的划分
这棵树最大的问题是所有节点的决策阈值都是笔者主观判断给出的。换句话说,我们怎么知道月收入2W是最佳的决策标准?失信次数大于10次是最好的判断依据?可能10次失信里某一次欠了一个亿那岂不是要老命了。
因此,我们需要借助更强大和更理性的算法找到最理想的的决策依据。
2. 回归、分类树是路径依赖问题,线性拆分问题
其实网上已经有很多文章写决策树,写得也很不错。笔者不打算在数学推导上浪费时间,只提一个很容易被忽略的性质:其实**决策树也好,回归树也好,都是路径依赖问题**,即下一步的决策取决于上一步已经获得的信息。**这也是传统技术派的观点,即过去可以代表未来**。
为什么路径依赖这条性质十分重要呢?因为**很多金融问题并不是路径依赖的**,如果依靠路径依赖的模型解决非路径依赖的问题那就是牛头不对马嘴。有没有非路径依赖的模型呢?有,蒙特卡洛模拟,随机游走实验这类方式就不是路径依赖问题,即下一步怎么走是完全独立的,和上一步无关。
其次是线性拆分问题,树的分裂是基于递归二分法,即给定某个阈值,每次采取二叉树的形式分裂。眼尖的人可能发现了,给定的某个阈值导致数据拆分时永远是方形的(例如图三)。而如果数据是非线性分割的,树算法就很容易出现偏差,例如图四中点A本来属于2类,但却被分类算法错误的分进4类中。
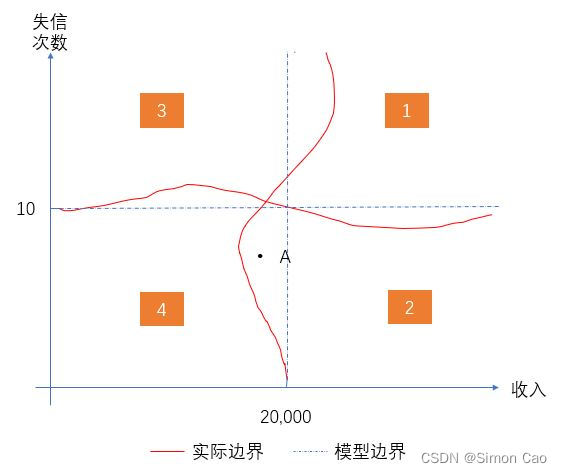
图四:线性切分导致偏差
3. Python实现
Python的sklearn就可以实现算法,也比较简单,但可视化上好一顿折腾:
先导入需要模块:
import tushare as ts
import pandas as pd
from sklearn import tree
import graphviz
如果电脑上完全没有graphviz这个模块,除了pip,还要安装graphviz的一个插件并且将其配置到环境变量里,不然不能输出最后的可视化PDF文件。安装和配置过程可以参考这篇知乎文章:Graphviz安装及使用-决策树可视化 - 知乎,笔者亲测有效。(graphviz出了很多版本,可以随便挑个旧版本的EXE文件下载安装)
数据方面笔者通过Tushare金融数据接口拿了今年11月4号的交易数据,下面获取一下数据:
pro = ts.pro_api("token")
df = pro.daily(trade_date='20221104')
ts_code trade_date open high low close pre_close change pct_chg vol amount
0 000001.SZ 20221104 10.40 10.85 10.39 10.82 10.44 0.38 3.6398 1776112.23 1903720.944
1 000002.SZ 20221104 13.58 14.09 13.55 14.04 13.64 0.40 2.9326 1077514.38 1500447.963
2 000004.SZ 20221104 8.75 8.92 8.72 8.86 8.76 0.10 1.1416 11770.00 10392.991
3 000005.SZ 20221104 1.69 1.71 1.68 1.71 1.69 0.02 1.1834 78672.00 13352.921
4 000006.SZ 20221104 3.75 3.83 3.73 3.82 3.74 0.08 2.1390 89775.00 34065.087
... ... ... ... ... ... ... ... ... ... ... ...
4966 873122.BJ 20221104 11.84 11.97 11.71 11.91 11.84 0.07 0.5912 7143.14 8472.178
4967 873169.BJ 20221104 6.74 6.95 6.71 6.85 6.73 0.12 1.7831 7576.40 5188.436
4968 873223.BJ 20221104 3.79 3.83 3.77 3.82 3.79 0.03 0.7916 10879.34 4147.043
4969 873527.BJ 20221104 9.25 9.38 9.22 9.35 9.25 0.10 1.0811 4454.14 4150.398
4970 689009.SH 20221104 33.45 34.35 33.10 34.18 33.20 0.98 2.9518 54280.39 183483.029
3.1 回归树
构建树的代码比较简单,笔者这里回归了涨跌幅和成交量及成交额, 仅作演示:
mod = tree.DecisionTreeRegressor(max_leaf_nodes=10)
result = mod.fit(df.iloc[:,9:], df.iloc[:,8]) # mod.fit(x, y)
其中, DecisionTreeRegressor()参数设置如下:
DecisionTreeRegressor(
criterion='mse', # 'MSE'均方误差, 'friedman_mse'费尔德曼均方误差;'mae'绝对离差
max_depth=2,
max_features=None,
max_leaf_nodes=None,
min_impurity_decrease=0.0, # #限制信息增益的大小,信息增益小于设定值分枝不会发生
min_impurity_split=None, # #节点必须含有最小信息增益再划分
min_samples_leaf=1, # 叶节点最少包含样本的个数
min_samples_split=2, # #节点必须包含训练样本的个数
min_weight_fraction_leaf=0.0,
presort=False,
random_state=None,
splitter='best'
)
都比较好理解,不过参数的详细解释在官网技术文档:sklearn.tree.DecisionTreeRegressor
笔者友情提示,如果数据集很大最好设置一下分裂的最大限制,不然会得到一颗“参天大树”,笔者看了大概有几千个叶节点吧,下如图:
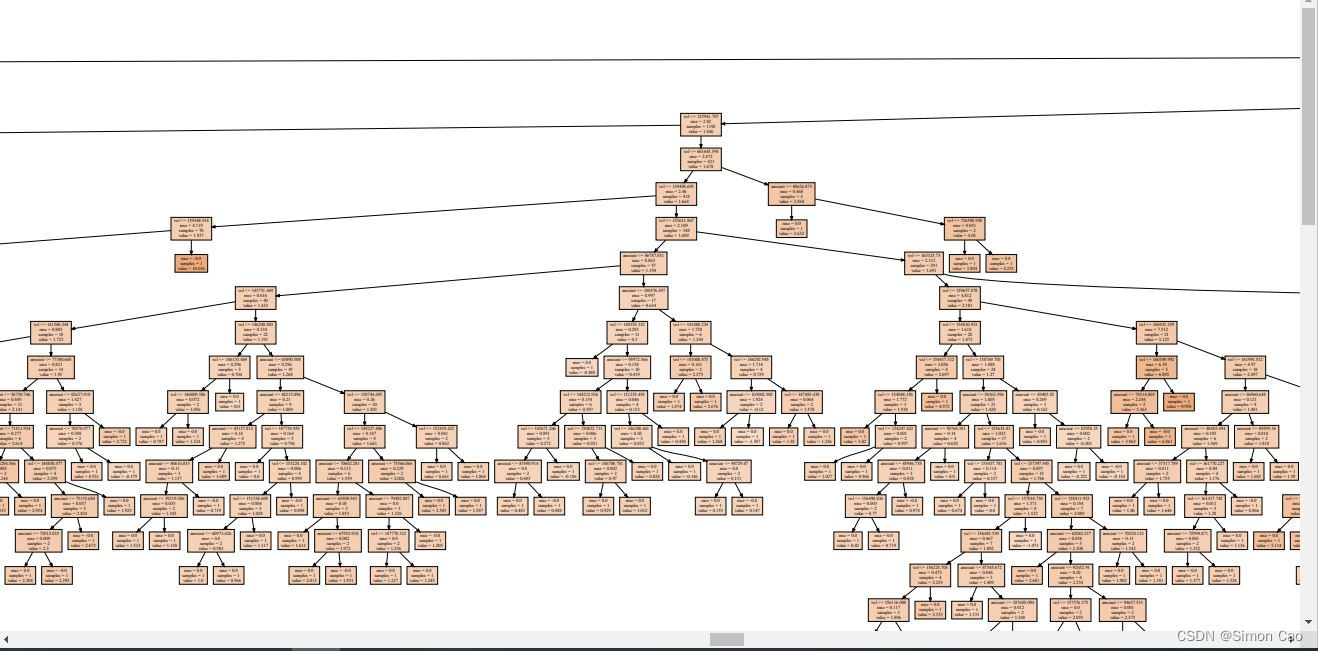
图五:不设置分裂限制(部分)
笔者设置了分裂节点限制,接下来可视化:
nodes = tree.export_graphviz(result, feature_names=["vol","amount"], filled=True)
graph = graphviz.Source(nodes)
graph.render(r"tree2") # 可视化生成一个PDF文件
得到:
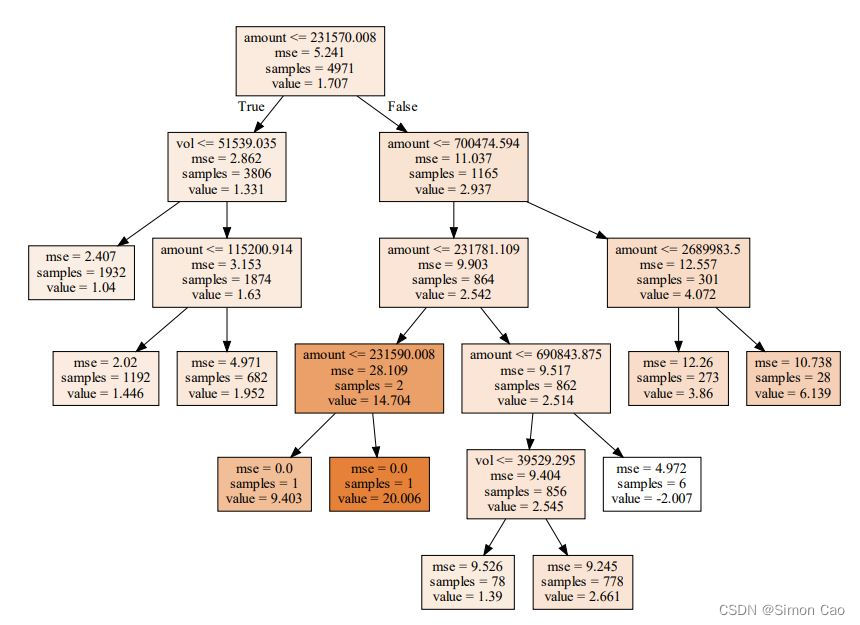
图六:设置分裂限制(max_leaf_nodes=10)
可以看到,一些叶节点的样本量非常小(如左三和左四叶节点),说明还是有点过度分裂了,再缩小限制,设max_leaf_nodes=4,则:
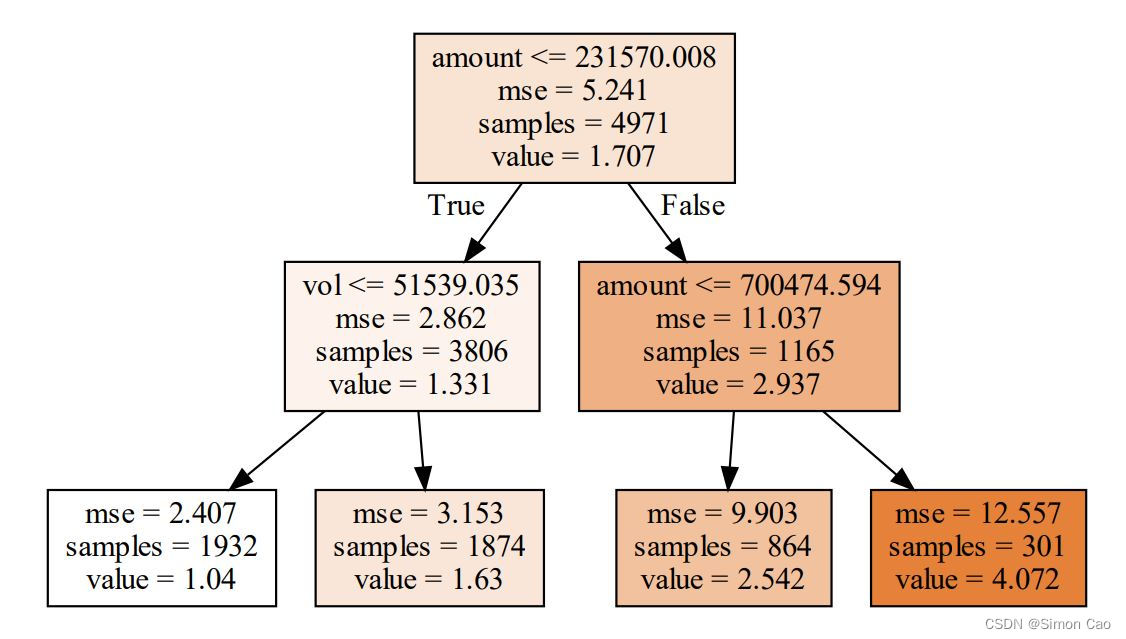
图七:设置分裂限制(max_leaf_nodes=4)
每个根节点的参数分别为:阈值,该根节点数据的MSE,该节点的样本量,该节点的期望值。
每个叶节点的参数为:该节点样本的MSE,样本量和期望值。
3.2 分类树
决策树的数理是对离散因变量进行分类,因此需要将之前回归的涨跌幅转换成哑变量:
df["pct_chg"][(df["pct_chg"]>0)]=1 # 上涨
df["pct_chg"][df["pct_chg"]<=0]=0 # 下跌
和刚刚一样实例化方法然后传数据参数进模型拟合:
mod = tree.DecisionTreeClassifier()(max_leaf_nodes=4)
result = mod.fit(df.iloc[:,9:], df.iloc[:,8]) # mod.fit(x, y)
其中, DecisionTreeClassifier()参数设置如下:
tree.DecisionTreeClassifier(
criterion=’gini’, # gini基尼系数或者entropy信息熵
splitter=’best’, # best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中,默认的”best”适合样本量不大的时候,而如果样本数据量非常大,此时决策树构建推荐”random”
max_depth=None, # int or None, optional (default=None) 设置决策随机森林中的决策树的最大深度,深度越大,越容易过拟合,推荐树的深度为:5-20之间
max_feature=None, # None(所有),log2,sqrt,N 特征小于50的时候一般使用所有的
min_samples_split=2, # 设置结点的最小样本数量,当样本数量可能小于此值时,节点将不会在划分
min_samples_leaf=1, # 限制了叶子节点最少的样本数,如果某叶节点数目小于g该数,则会和兄弟节点一起被剪枝
min_weight_fraction_leaf=0.0, # 这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝默认是0,就是不考虑权重问题
max_features=None,
random_state=None,
max_leaf_nodes=None, # 最大叶节点数
min_impurity_decrease=0.0,
min_impurity_split=None,
class_weight=None,
presort=False
)
参数的详细解释在官网技术文档:
可视化与之前类似,就不再展示图片了:
nodes = tree.export_graphviz(result, feature_names=["vol","amount"], filled=True)
graph = graphviz.Source(nodes)
graph.render(r"tree2") # 可视化生成一个PDF文件
4. R语言实现
笔者不得不说,比起Python,R语言方便不少,**尤其可视化这块,非常友好**。接下来笔者用之前上学时的一次作业进行展示,任务主要是对信用卡贷款违约进行分析。
R语言的决策树主要通过rpart模块实现,可视化通过rpart.plot实现,没有安装的需要install.package()一下,下面导入模块:
library(rpart)
library(rpart.plot)
导入数据,简单查看变量及其统计数据:
df <- read.csv("CREDIT.csv")
summary(df)
Customer Default WeeklyIncome EmploymentDuration
Min. : 1.00 Length:140 Min. :-0.80700 Min. :-1.83300
1st Qu.: 35.75 Class :character 1st Qu.:-0.61100 1st Qu.:-0.90700
Median : 70.50 Mode :character Median :-0.33200 Median : 0.01900
Mean : 70.50 Mean :-0.02482 Mean : 0.06516
3rd Qu.:105.25 3rd Qu.: 0.15100 3rd Qu.: 0.48200
Max. :140.00 Max. : 5.59500 Max. : 2.79600
WeeklySpend Children Age Education
Min. :-1.42100 Min. :-0.498000 Min. :-1.642000 Min. :-2.82600
1st Qu.:-0.62975 1st Qu.:-0.498000 1st Qu.:-0.814250 1st Qu.:-0.68700
Median :-0.15400 Median :-0.498000 Median :-0.028000 Median : 0.13000
Mean :-0.04405 Mean :-0.008943 Mean :-0.003114 Mean : 0.04616
3rd Qu.: 0.26800 3rd Qu.:-0.378250 3rd Qu.: 0.737000 3rd Qu.: 0.69200
Max. : 3.64700 Max. : 4.290000 Max. : 1.756000 Max. : 3.44900
可以看到,违约情况是非结构化数据,其它所有数据在当时已经被标准化了。
将标签转换成哑变量:
df$Default[df$Default=="No Default"] <- 0
df$Default[df$Default=="Default"] <- 1
4.1 回归树
由于违约状况转换回来是离散因变量,因此这里回归的因变量是个哑变量,也就是说最后计算的结果是违约概率(。
就两行代码,一行生成拟合回归树,一行可视化,非常简单。笔者想想上面Python的反人类操作简直快吐血了。。
fit.tree <- rpart(Default ~ ., data = df, method="anova")
rpart.plot(fit.tree, type = 1) # type为图表展示的类型
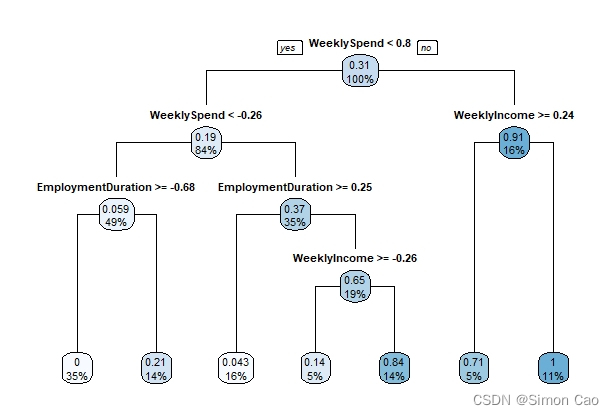
图八:R语言回归树
4.1.1 通过拟合优度确认树的剪枝参数
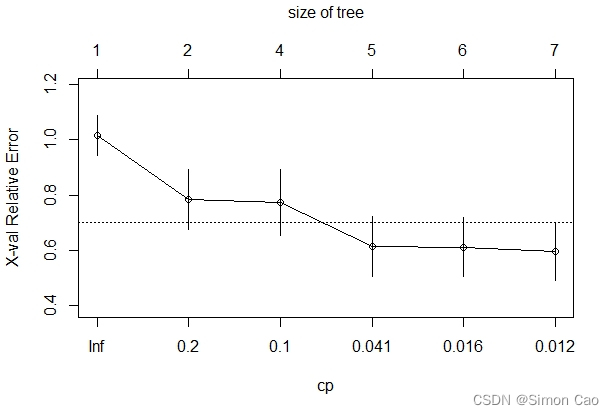
通过plotcp可以查看最佳剪枝参数:
printcp(fit.tree)
plotcp(fit.tree)
如图九, y轴展示了不同规模的树下进行交叉验证时error的大小。可以看到,在tree size为5时其误差最小,拟合优度最佳,此时cp参数(Complexity parameter, 即复杂程度)为0.041:
图九:回归树拟合优度图
于是我们可以在回归树内设置复杂参数:
fit.prune <- prune(fit.tree, cp=0.041)
rpart.plot(fit.prune, type = 1)
运行得:
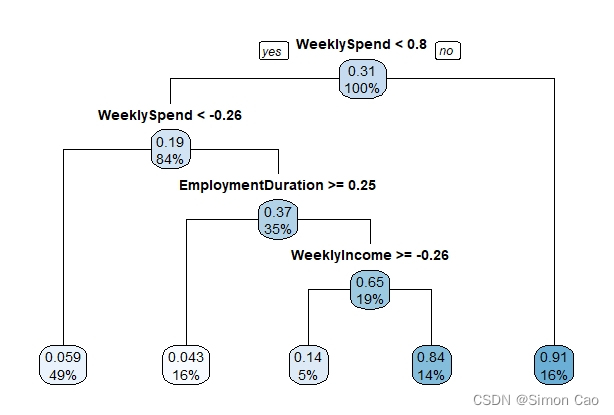
图十:违约分析回归树(参数cp=0.041)
4.1.2 叶节点的含义
R语言的树非常简洁,因此没有像Python把所有变量是什么一个个标出来。在回归树下叶节点会有两个参数分别代表该节点期望值和概率,以左一叶节点为例,0.059代表落在该节点的数据违约概率的期望值是5.9%,49%指49%的样本落在这个节点上。
4.2 分类树
R语言分类树就在回归树基础上加上把anova参数改成class:
fit.tree <- rpart(Default ~ ., data = df, method="class")
printcp(fit.tree)
plotcp(fit.tree)
可以看到,拟合优度图显示最佳的cp值为0.03:
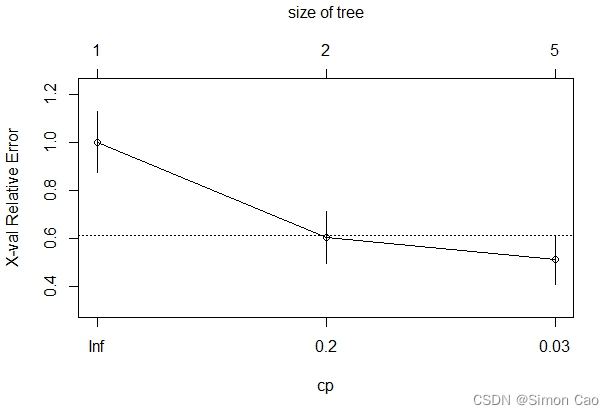
图十一:分类树拟合优度图
采用优化的参数拟合并展示:
fit.prune <- prune(fit.tree, cp=0.03)
rpart.plot(fit.prune, type = 1)

图十二:违约分析分类树(参数cp=0.03)
简单说下叶节点含义,可以看到,分类树比回归树多了一个参数,从上到下依次是:节点类别,该节点内样本中标签属于该节点类别的百分比,以及该节点样本占总体样本量的百分比。以右一叶节点为例,该节点标签为违约,该节点内91%的样本都是违约样本,该节点样本占总体样本量的16%。
5. 总结
以后我再也不敢用Python做决策树了:

Finally, I'm the clown
版权归原作者 Simon Cao 所有, 如有侵权,请联系我们删除。