数学建模比赛中的预测方法
前言
大家好！ φ(*￣0￣) 2022年的比赛将在九月份进行，通常每个学校都会六月或七月给本校的学生发通知，并把那些对这个比赛感兴趣的同学进行培训，讲解数模比赛中可能会遇到的一些数学模型和求解模型的方法。在培训过程中也是非常艰苦的，因为在培训工程中，安排出来的时间一般都不影响上课时间，设在中午大家午休的时候，那这样的话就是说每天中午都是不得睡觉，这就很苦了。不过，想想：如果坚持到最后，写出了论文并拿到了国奖，那这培训的苦都值得了。
好了，废话少说，进入今天的主题：数学建模之预测。
移动平均法
移动平均法的基本原理：通过移动平均消除时间序列中的不规则变动和其他变动，从而揭示出时间序列的长期趋势。移动平均法根据预测时使用的各元素的权重不同，可以分为：简单移动平均和加权移动平均。
###简单移动平均
我们刚才说了平均法就是各元素的权重不同，那么简单移动平均就是个元素权重相同。
简单的移动平均的计算公式如下：
F
t
=
(
A
t
−
1
+
A
t
−
1
+
A
t
−
3
+
.
.
.
A
t
−
n
)
/
n
F_t=(A_t-_1+A_t-_1+A_t-_3+...A_t-_n)/n
Ft=(At−1+At−1+At−3+...At−n)/n
式中，
F
t
F_t
Ft 对下一期的预测值；
n–移动平均的时期个数；
A
t
−
1
A_t-_1
At−1为前期实际值；
A
t
−
n
A_t-_n
At−n为前n期的实际值。
简单明了的人话说就是求平均值。
✨✨✨下面给大家带入例子来认识一下吧！
首先准备一份数据，随便一份数据都行的。我这里用年份-供水量的部分数据表。
那下面教一下大家怎么操作：
- 打开Excel,找到数据分析工具。在初次使用时会发现在Excel相应位置中找不到这一选项，其原因在于在安装Office办公集成软件或Microsoft Excel时，一般使用的是“自动”或“典型”安装。为此，需要使用者自己加载这一功能。第一步：点开文件->>更多->>选项->>如图二所示
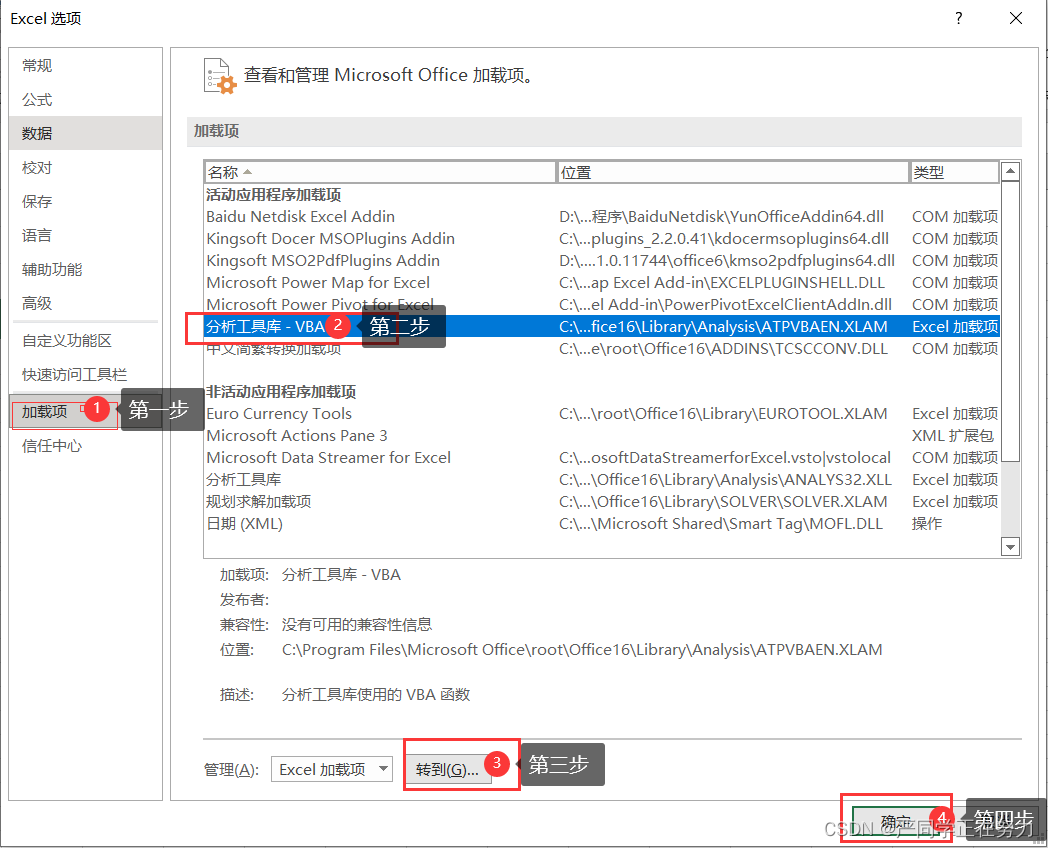第二步确定后，在工具栏就可以看到数据分析。
第三步在“工具”菜单中选择“数据分析”选项，从其“分析工具”列表中选择“移动平均”，回车进入该工具对话框，如图四所示。这里解释一下： 在“输入区域(I)”框中输入时间序列数据所在的区域，本例为“B2:B11”； 在“间隔(N)”框中输入移动步长，本例先进行3项移动平均。 在“输出区域(O)”框中，输入“C2”；选择“图表输出©”复选框。这里需要注意的是，“输出区域(O)”框中必须输入“C2”，这样输出的结果才能与原时间序列相对应。 完成以上设置后，回车确认，即可得到所需结果，重复以上操作可得到3期移动平均序列，如图五所示。
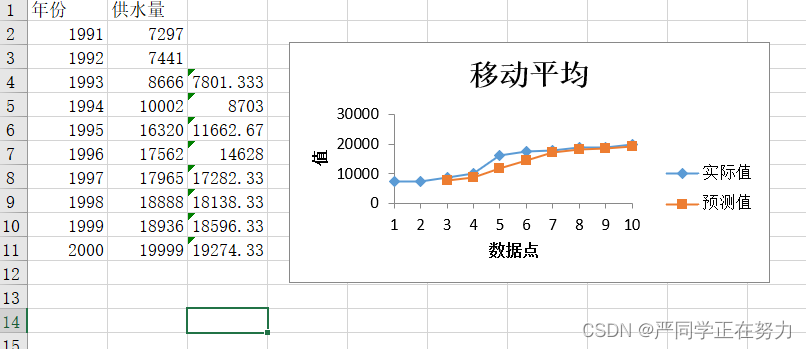结果解释与分析： C列为3期移动平均产生的新时间序列。可以看出现象发展的变动趋势
指数平滑
指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值（下一期的预测值），配合一定的时间序列预测模型对现象的未来进行预测，其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。
指数平滑法的基本公式是：
S
t
=
a
Y
t
−
1
+
(
1
−
a
)
S
t
−
1
S_t=a Y_t-_1+(1-a)S_t-_1
St=aYt−1+(1−a)St−1
式中，
S
t
S_t
St是时间t-1的平滑值，时间t的预测值；
Y
t
−
1
Y_t-_1
Yt−1时间t-1的实际值；
S
t
−
1
S_t-_1
St−1时间t-1的预测值；
a平滑常数，其取值范围为[0,1]；
✨✨✨下面给大家带入例子来认识一下吧！
仍然是年份-供水量数据我们来进行指数平滑实验操作。
第一步：打开指数平滑对话窗，如图七所示输入区域选择B2-B11，阻尼系数我们这里选择0.6，输出区域选择C3。得出结果如图八所示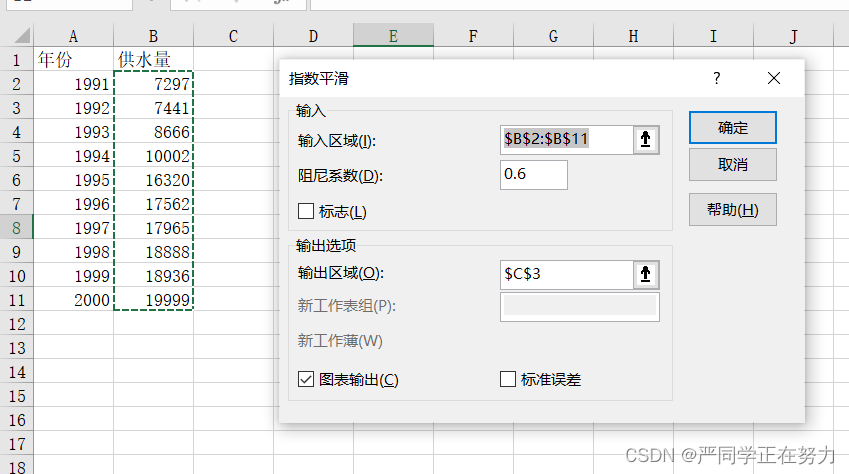
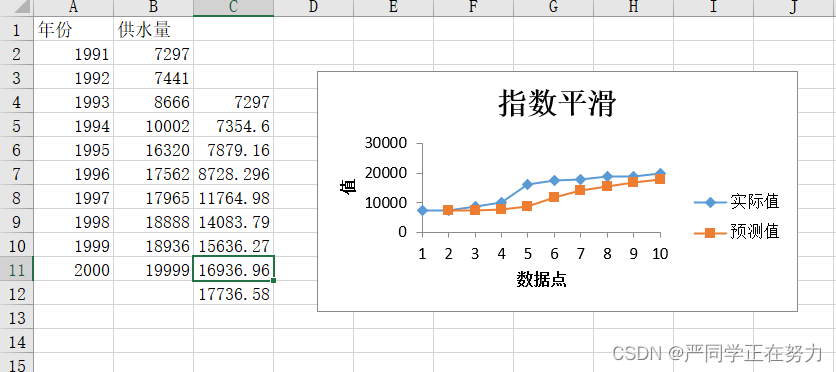
在这里解释一下阻尼系数是干什么的：
平滑指数的公式是这样的
S
t
=
a
Y
t
−
1
+
(
1
−
a
)
S
t
−
1
S_t=a Y_t-_1+(1-a)S_t-_1
St=aYt−1+(1−a)St−1
a平滑常数=阻尼系数， 图九展示的函数就是平滑指数的公式了。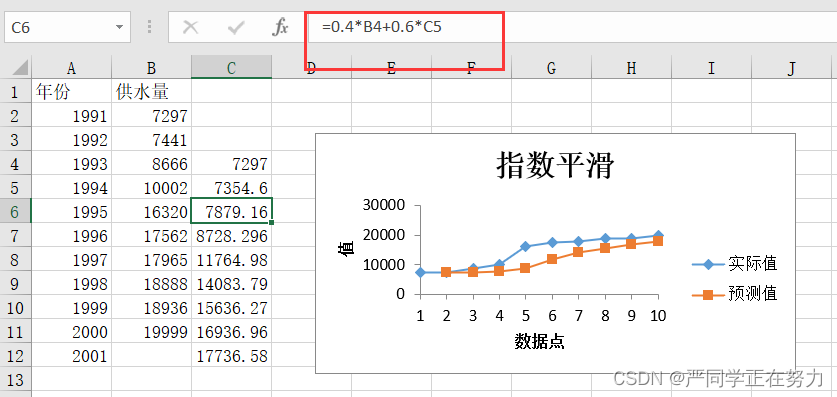
🌷🌷🌷🌷🌷好了，今天就分享到这里吧！祝愿各个参赛选手都拿国奖！加油！！
版权归原作者 严同学正在努力 所有， 如有侵权，请联系我们删除。