✨博客主页:米开朗琪罗~🎈
✨博主爱好:羽毛球🏸
✨年轻人要:Living for the moment(活在当下)!💪
🏆推荐专栏:【图像处理】【千锤百炼Python】【深度学习】【排序算法】
目录
😺一、引言
类似于人脑的注意力感知,那卷积神经网络能否也能产生注意力效果呢?答案是:可以!
SE_Block是SENet的子结构,作者将SE_Block用于ResNeXt中,并在ILSVRC 2017大赛中拿到了分类任务的第一名,在ImageNet数据集上将top-5 error降低到2.251%,比2016年的最好成绩提高了约25%。
论文链接:Squeeze-and-Excitation Networks
开源代码:https://github.com/hujie-frank/SENet
😺二、网络结构
作者研究了网络设计通道之间的关系,引入了一个新的结构单元SE_Block,其目标是通过显式地建模网络演化特征通道之间的相互依赖关系来提高网络生成的表示的质量。为此,作者提出了一种机制,允许网络执行特征重新校准,通过这种机制,它可以学习使用全局信息来选择性地强调信息性特征,并抑制不太可靠的特征。
🐶2.1 SE_Block结构图
SE_Block(SQUEEZE-AND-EXCITATION BLOCKS)主要包含两部分,分别是Squeeze和Excitation。
结构中
F
t
r
F_{tr}
Ftr的输入为
X
X
X,且
X
∈
R
H
′
×
W
′
×
C
′
X\in \mathbb{R}^{H^{'}\times W^{'}\times C^{'}}
X∈RH′×W′×C′,输出为
U
U
U,且
U
∈
R
H
×
W
×
C
U\in \mathbb{R}^{H\times W\times C}
U∈RH×W×C。
我们将
F
t
r
F_{tr}
Ftr视为一个简单的卷积操作,用式子
V
=
[
v
1
,
v
2
,
⋯
,
v
C
]
V=[v_{1},v_{2},\cdots ,v_{C}]
V=[v1,v2,⋯,vC]表示,其中
v
c
v_{c}
vc表示第
c
c
c个卷积核,输出用式子
U
=
[
u
1
,
u
2
,
⋯
,
u
C
]
U=[u_{1},u_{2},\cdots ,u_{C}]
U=[u1,u2,⋯,uC]表示,则有:
u
c
=
v
c
∗
X
=
∑
s
=
1
C
′
v
c
s
∗
x
s
u_{c}=v_{c}\ast X=\sum_{s=1}^{C^{'}}v_{c}^{s}\ast x^{s}
uc=vc∗X=s=1∑C′vcs∗xs
其中
∗
\ast
∗表示卷积,
v
c
=
[
v
c
1
,
v
c
2
,
⋯
,
v
c
C
′
]
v_{c}=[v_{c}^{1},v_{c}^{2},\cdots ,v_{c}^{C^{'}}]
vc=[vc1,vc2,⋯,vcC′],
X
=
[
x
1
,
x
2
,
⋯
,
x
C
′
]
X=[x^{1},x^{2},\cdots ,x^{C^{'}}]
X=[x1,x2,⋯,xC′],且
u
c
∈
R
H
×
W
u_{c}\in R^{H\times W}
uc∈RH×W,
v
c
s
v_{c}^{s}
vcs是一个2D空间卷积,为了简化公式,作者简化了偏置项。
由于输出是通过所有通道的求和产生的,因此通道相关性隐式地嵌入在
v
c
v_{c}
vc中,但与滤波器捕获的局部空间相关性相纠缠。我们期望通过显式地建模通道的相互依赖性来增强卷积特征的学习,从而使网络能够提高其对信息特征的敏感性,这些信息特征可以被后续转换利用。因此,我们希望为其提供获取全局信息的途径,并在输入下一个转换之前,分两步(Sequeeze and Excitation)重新校准滤波器响应。

🐶2.2 Squeeze:Global Information Embedding
作者首先考虑输出特征图中的每个信道的信号。每个学习到的滤波器都与一个局部感受野一起工作,因此转换输出
U
U
U的每个单元都无法利用该区域之外的上下文信息。
为了解决这个问题,作者建议将全局空间信息压缩到信道描述符中。这是通过使用全局平均池生成通道统计信息来实现的。准确地说,
z
∈
R
C
z\in R^{C}
z∈RC是对特征
U
U
U在空间维度
H
×
W
H\times W
H×W执行全局平均池化后的结果,因此
z
z
z的每一个元素表示如下:
z
c
=
F
s
q
(
u
c
)
=
1
H
×
W
∑
i
=
1
H
∑
j
=
1
W
u
c
(
i
,
j
)
z_{c}=F_{sq}(u_{c})=\frac{1}{H\times W}\sum_{i=1}^{H}\sum_{j=1}^{W}u_{c}(i,j)
zc=Fsq(uc)=H×W1i=1∑Hj=1∑Wuc(i,j)
因此,Squeeze操作就是在得到
U
U
U(多个特征图)之后采用全局平均池化操作对每一个特征图进行牙所,使其
C
C
C个特征图最后变成
1
×
1
×
C
1×1×C
1×1×C的实数数列。
🐶2.3 Excitation: Adaptive Recalibration
为了利用Squeeze操作中聚合的信息,我们需要继续执行第二个操作Excitation,目的是完全捕获通道依赖关系。为了实现这一目标,该功能必须满足两个标准:第一,它必须操作灵活(尤其是它必须能够学习通道之间的非线性关系),第二,它必须学习非互斥关系,因为我们希望多个通道都能被加强(而不是类似one-hot那种仅加强了某一个通道特征)。为了满足这些标准,作者选择使用带有sigmoid 激活的简单门控机制。
为了满足上述两个条件,作者采用了下面的变换形式:
s
=
F
e
x
(
z
,
W
)
=
σ
(
g
(
z
,
W
)
)
=
σ
(
W
2
δ
(
W
1
z
)
)
s=F_{ex}(z,W)=\sigma (g(z,W))=\sigma (W_{2}\delta (W_{1}z))
s=Fex(z,W)=σ(g(z,W))=σ(W2δ(W1z))
上式中,
σ
\sigma
σ表示sigmoid激活函数,
δ
\delta
δ表示relu激活函数,其中
W
2
∈
R
C
r
×
C
W_{2}\in \mathbb{R}^{\frac{C}{r}\times C}
W2∈RrC×C,
W
2
∈
R
C
×
C
r
W_{2}\in \mathbb{R}^{C\times \frac{C}{r}}
W2∈RC×rC。
为了限制模型的复杂性并使其通用化,作者使用两个FC层来对选通机制进行参数化,即具有降维率
r
r
r的降维层,一个ReLU,然后是一个维度升高层,再转到输出特征图的通道维度。通过使用激活重新缩放特征图来获得Block的最终输出。
得到
s
s
s后,可以通过下式得到SE_Block的最终输出:
x
~
c
=
F
s
c
a
l
e
(
u
c
,
s
c
)
=
s
c
u
c
\tilde{x}_{c}=F_{scale}(u_{c},s_{c})=s_{c}u_{c}
x~c=Fscale(uc,sc)=scuc
其中
X
~
=
[
x
~
1
,
x
~
2
,
⋯
,
x
~
C
]
\tilde{X}=[\tilde{x}_{1},\tilde{x}_{2},\cdots ,\tilde{x}_{C}]
X~=[x~1,x~2,⋯,x~C],
u
c
∈
R
H
×
W
u_{c}\in R^{H\times W}
uc∈RH×W,
F
s
c
a
l
e
F_{scale}
Fscale是通道上的乘积。
😺三、模块迁移
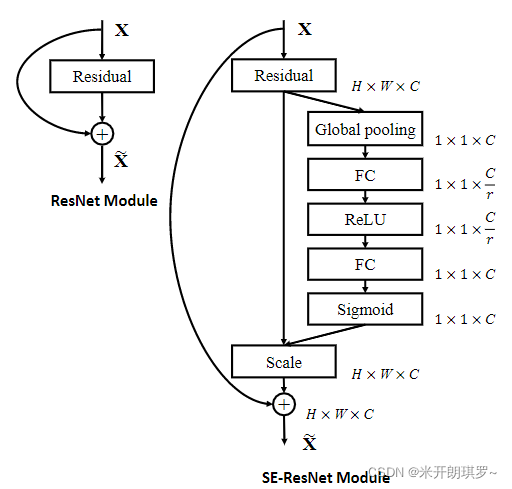
下图是将SE_Block迁移到Inception网络与ResNet中的结构图: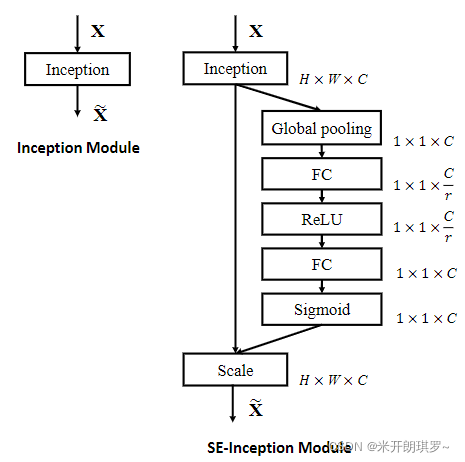
😺四、总结
作者提出了一个可移植性非常高的通道注意力模块SE_Block,并在各种经典神经网络中表现了不错的性能。
版权归原作者 米开朗琪罗~ 所有, 如有侵权,请联系我们删除。